giúp mik bài 7 và bài8

Mọi người giúp mình bài 7 và bài8 với ạ
Bài 8:
a: \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
c: \(8-12x+6x^2-x^3=\left(2-x\right)^3\)
Mấy bạn giải giúp mik bài 7 và bài 9 vs ạ
Bài 7:
a)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge m+1\\x\ge\dfrac{m}{4}\end{matrix}\right.\)
TH1: \(m+1< \dfrac{m}{4}\Rightarrow m< -\dfrac{4}{3}\)
\(\Rightarrow x\ge\dfrac{m}{4}\)\(\Rightarrow x\in\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([\dfrac{m}{4};+\)\(\infty\)\()\)
\(\Leftrightarrow\dfrac{m}{4}\ge0\Leftrightarrow m\ge0\) kết hợp với \(m< -\dfrac{4}{3}\Rightarrow m\in\varnothing\)
TH2:\(m+1\ge\dfrac{m}{4}\Rightarrow m\ge-\dfrac{4}{3}\)
\(\Rightarrow x\ge m+1\)\(\Rightarrow\)\(x\in\)\([m+1;+\)\(\infty\))
Để hàm số xác định với mọi x dương \(\Leftrightarrow\)\(\left(0;+\infty\right)\subset\)\([m+1;\)\(+\infty\)\()\)
\(\Leftrightarrow m+1\le0\Leftrightarrow m\le-1\) kết hợp với \(m\ge-\dfrac{4}{3}\)
\(\Rightarrow m\in\left[-\dfrac{4}{3};-1\right]\)
Vậy...
b)ĐKXĐ:\(\left\{{}\begin{matrix}x\ge2-m\\x\ne-m\end{matrix}\right.\)\(\Rightarrow x\in\)\([2-m;+\)\(\infty\)) (vì \(-m< 2-m\))
Để hàm số xác ddingj với mọi x dương
\(\Leftrightarrow\left(0;+\infty\right)\subset\)\([2-m;+\)\(\infty\))
\(\Leftrightarrow2-m\le0\Leftrightarrow m\ge2\)
Vậy...
Bài 9:
a)Đặt \(f\left(x\right)=x^2+2x-2\)
TXĐ:\(D=R\)
TH1:\(x\in\left(-\infty;-1\right)\)
Lấy \(x_1;x_2\in\left(-\infty;-1\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2\)
Vì \(x_1;x_2\in\left(-\infty;-1\right)\Rightarrow x_1+x_2< -1+-1=-2\)\(\Leftrightarrow x_1+x_2+2< 0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;-1\right)\)
TH2:\(x\in\left(-1;+\infty\right)\)
Lấy \(x_1;x_2\in\left(-1;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2+2x_1-2-\left(x_2^2+2x_2-2\right)}{x_1-x_2}=x_1+x_2+2>0\)
Suy ra hàm đb trên \(\left(-1;+\infty\right)\)
Vậy...
b)Đặt \(f\left(x\right)=\dfrac{2}{x-3}\)
TXĐ:\(D=R\backslash\left\{3\right\}\)
TH1:\(x\in\left(-\infty;3\right)\)
Lấy \(x_1;x_2\in\left(-\infty;3\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(-\infty;3\right)\Rightarrow x_1-3< 0;x_2-3< 0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(-\infty;3\right)\)
TH2:\(x\in\left(3;+\infty\right)\)
Lấy \(x_1;x_2\in\left(3;+\infty\right)\)\(:x_1\ne x_2\)
Xét \(I=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{\dfrac{2}{x_1-3}-\dfrac{2}{x_2-3}}{x_1-x_2}=\dfrac{-2}{\left(x_1-3\right)\left(x_2-3\right)}\)
Vì \(x_1;x_2\in\left(3;+\infty\right)\Rightarrow x_1-3>0;x_2-3>0\Rightarrow\left(x_1-3\right)\left(x_2-3\right)>0\)
\(\Rightarrow I< 0\)
Suy ra hàm nb trên \(\left(3;+\infty\right)\)
Vậy hàm nb trên \(\left(-\infty;3\right)\) và \(\left(3;+\infty\right)\)
giúp mik vs bài 7 và 8,9 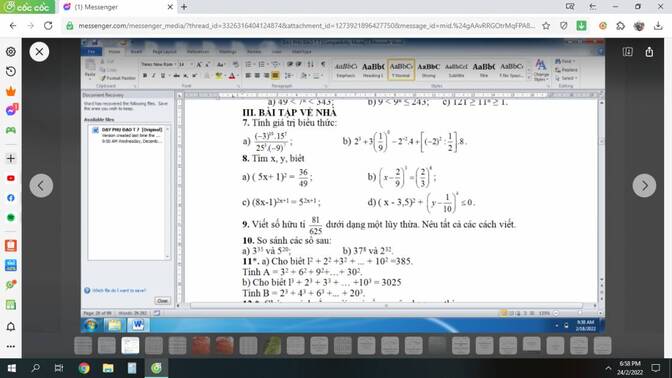
doi minh 1 lat nha

làm giúp mik phần b,c,d bài 7 và làm bài 8 nhé
d: Ta có: \(5n+12⋮n-3\)
\(\Leftrightarrow n-3\in\left\{1;-1;3;-3;9;-9;27;-27\right\}\)
hay \(n\in\left\{4;2;6;0;12;-6;30;-24\right\}\)
Bài8.Thu gọn,tìm bậc và hệ số của các đơn thức sau:
a) A=(-2a2c3).a2b
bài8
8:
a: Xét ΔAFB và ΔCFI có
góc FAB=góc FCI
góc AFB=góc CFI
=>ΔAFB đồng dạng với ΔCFI
b: Xét ΔEAB và ΔEKD có
góc EAB=góc EKD
góc AEB=góc KED
=>ΔEAB đồng dạng với ΔEKD
=>AB/KD=EA/EK
=>AB*EK=EA*KD
Giúp mik bài 7 bài 8 vẽ hộ mik hình bài 7 cảm ơn Trc ạ
xét tứ giác AFCD có EA=EC;ED=EF nên tứ giác AFCD là hình bình hành
Ai giúp mik trả lời bài 23 đến bài 52 với, trong sách nâng cao và phát triển lớp 7 tập 1. Mik xin cảm ơn
Bài 1: Rút gọn rồi so sánh các phân số sau
a, 3/5 và 33/55 b, 5/7 và 6/21 c, 5/7 và 20/28
giúp mik nhé thật ra là giúp cho bn mik.
bạn tham khảo :
Câu hỏi của hoang van binh - Toán lớp 4 - Học trực tuyến OLM
tham khảo :}
Câu hỏi của hoang van binh - Toán lớp 4 - Học trực tuyến OLM