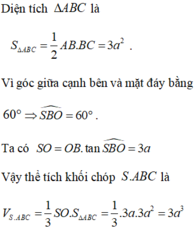tính dtxq và dttp của hình chóp tứ giác đều có cạnh đáy bằng cạnh bên

Những câu hỏi liên quan
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp A.
S
3
πa
2
2
B.
S
πa
2
2
C. S
2
πa
2
D.
S
πa
2
Đọc tiếp
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
A. S = 3 πa 2 2
B. S = πa 2 2
C. S = 2 πa 2
D. S = πa 2
Gọi O là tâm hình vuông của mặt đáy. Khi đó O cũng là tâm của mặt cầu. Ta có:
R 2 = S O 2 = a 2 - a 2 2 2 = a 2 2 S = 4 πR 2 = 2 πa 2
Đáp án C
Đúng 0
Bình luận (0)
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
Đọc tiếp
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp
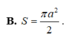
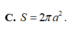
![]()
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
Đọc tiếp
Một hình chóp tứ giác đều có cạnh đáy bằng cạnh bên và bằng a. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
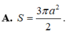
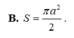
![]()
![]()
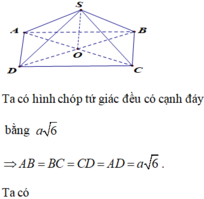
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng
a
6
, góc giữa cạnh bên và mặt đáy bằng
60
0
. Tính thể tích V của khối chóp S.ABC? A.
V
9
a
3
B.
V
2
a
3
C.
V
3
a
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a 6 , góc giữa cạnh bên và mặt đáy bằng 60 0 . Tính thể tích V của khối chóp S.ABC?
A. V = 9 a 3
B. V = 2 a 3
C. V = 3 a 3
D. V = 6 a 3
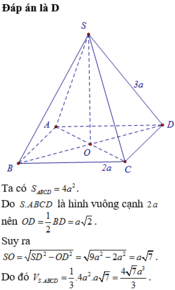
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng 3a. Tính thể tích V của khối chóp đã cho A.
V
4
7
a
3
6
B.
V
7
a
3
3
C.
V
4...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a và cạnh bên bằng 3a. Tính thể tích V của khối chóp đã cho
A. V = 4 7 a 3 6
B. V = 7 a 3 3
C. V = 4 7 a 3 2
D. V = 4 7 a 3 3
Một hình chóp tứ giác đều S.ABCD có cạnh bên SA 13cm và độ dài cạnh đáy là
5
2
. Tính thể tích của hình chóp tứ giác đều. A.
200
c
m
3
B.
150
c
m
3
C.
180
c
m
3
D.
210
c
m
3
Đọc tiếp
Một hình chóp tứ giác đều S.ABCD có cạnh bên SA = 13cm và độ dài cạnh đáy là 5 2 . Tính thể tích của hình chóp tứ giác đều.
A. 200 c m 3
B. 150 c m 3
C. 180 c m 3
D. 210 c m 3
Chọn đáp án A
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Pytago vào tam giác vuông ABC có:
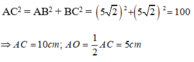
Áp dụng định lí Pytago vào tam giác vuông SAO có:
S O 2 = S A 2 - A O 2 = 13 2 - 5 2 = 144 nên SO = 12cm
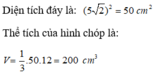
Đúng 0
Bình luận (0)
tính diện tích toàn phần của hình chóp tứ giác đều có cạnh đáy 25m và chiều cao mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 20cm
20 cm = 0,2 m
Diện tích toàn phần của hình chóp tứ giác đều là:
\(\dfrac12\cdot(4\cdot25)\cdot0,2+25^2=635(m^2)\)
Vậy: ...
\(\text{#}Toru\)
Đúng 2
Bình luận (0)
Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ và đường nối tâm hai đáy bằng \(a\). Tính độ dài cạnh bên và đường cao của mỗi mặt bên.
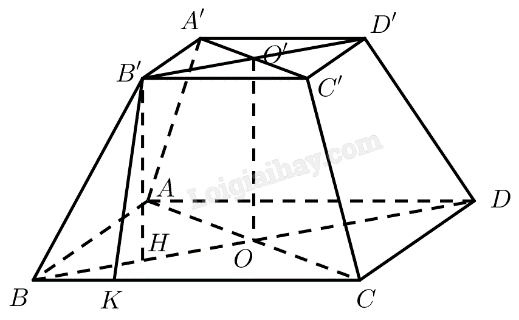
Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy.
Kẻ \(B'H \bot B{\rm{D}}\left( {H \in B{\rm{D}}} \right),B'K \bot BC\left( {K \in BC} \right)\)
\(\begin{array}{l}B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = 2a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = a\sqrt 2 \\B'D' = \sqrt {A'B{'^2} + A'{\rm{D}}{{\rm{'}}^2}} = a\sqrt 2 \Rightarrow B'O' = \frac{1}{2}B'{\rm{D'}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
\(OO'B'H\) là hình chữ nhật \( \Rightarrow OH = B'O' = \frac{{a\sqrt 2 }}{2},B'H = OO' = a\)
\( \Rightarrow BH = BO - OH = \frac{{a\sqrt 2 }}{2}\)
Tam giác \(BB'H\) vuông tại \(H\) có: \(BB' = \sqrt {B'{H^2} + B{H^2}} = \frac{{a\sqrt 6 }}{2}\)
\(BCC'B'\) là hình thang cân \( \Rightarrow BK = \frac{{BC - B'C'}}{2} = \frac{a}{2}\)
Tam giác \(BB'K\) vuông tại \(K\) có: \(B'K = \sqrt {BB{'^2} - B{K^2}} = \frac{{a\sqrt 5 }}{2}\)
Đúng 0
Bình luận (0)
Tính diện tích toàn phần của hình chóp tứ giác đều có cạnh đáy 25m và chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 20m
Sxq=1/2*24*4*20=12*80=960m2
Stp=960+25^2=1585m2
Đúng 0
Bình luận (0)