Đáp án A

Ta có, giả thiết  log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính  R 1 = 2

Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m  là đường tròn tâm I(-2;-3); R 2 = m  

Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9

Đáp án A

Ta có, giả thiết

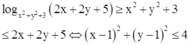
là miền trong đường tròn tâm I(1;1) bán kính R₁ = 2

Và 

Bạn tham khảo nhé!

Câu hỏi của Lê VĂn Chượng - Toán lớp 10 - Học toán với OnlineMath

a) x² - 8x + 19 = ( x² - 8x + 16 ) + 3 = ( x - 4 )² + 3 ≥ 3 > 0 ∀ x ( đpcm )

b) x² + y² - 4x + 2 = ( x² - 4x + 4 ) + y² - 2 = ( x - 2 )² + y² - 2 ≥ -2 ∀ x, y ( chưa cm được -- )

c) 4x² + 4x + 3 = ( 4x² + 4x + 1 ) + 2 = ( 2x + 1 )² + 2 ≥ 2 > 0 ∀ x ( đpcm )

d) x² - 2xy + 2y² + 2y + 5 = ( x² - 2xy + y² ) + ( y² + 2y + 1 ) + 4 = ( x - y )² + ( y + 1 )² + 4 ≥ 4 > 0 ∀ x, y ( đpcm )

a: ta có: \(A=x^2-3x+10\)

\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{31}{4}\)

\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}>0\forall x\)

b: Ta có: \(B=x^2-5x+2021\)

\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{8015}{4}\)

\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{8015}{4}>0\forall x\)

Đáp án: C

x 2  + y 2  - 4x + 2y - m + 1 = 0 ⇔ (x - 2 ) 2  + (y + 1 ) 2  = m + 4 (*)

Để (*) là phương trình của một đường tròn thì: m + 4 > 0 ⇔ m > -4

Bài 1:

$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$ 

$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$

$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$

Bài 2:
$8x^3-32y-32x^2y+8x=0$

$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$

$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$

$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)

$\Leftrightarrow x=4y$

Khi đó:

$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$

Bài cuối $x^21$ không rõ. Bạn xem lại.