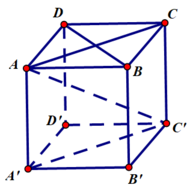
Cho hình lập phương ABCD.EFGH. Phân tích vecto AE theo vecto AC, AF, AH

Những câu hỏi liên quan
1.Cho hình lập phương ABCD.EFGH. Hãy tính góc giữa 2 vecto AF và vecto EG
2.Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ,CD) bằng?
1. Do \(EG||AC\Rightarrow\widehat{\left(\overrightarrow{AF};\overrightarrow{EG}\right)}=\widehat{\left(\overrightarrow{AF};\overrightarrow{AC}\right)}=\widehat{FAC}\)
Mà \(AF=AC=CF=AB\sqrt{2}\Rightarrow\Delta ACF\) đều
\(\Rightarrow\widehat{FAC}=60^0\)
2.
Do I;J lần lượt là trung điểm SC, BC \(\Rightarrow IJ\) là đường trung bình tam giác SBC
\(\Rightarrow IJ||SB\)
Lại có \(CD||BA\Rightarrow\widehat{\left(IJ;CD\right)}=\widehat{SB;BA}=\widehat{SBA}=60^0\) (do các cạnh của chóp bằng nhau nên tam giác SAB đều)
Đúng 0
Bình luận (0)
cho hình lập phương abcd và efgh cạnh a. Tính hđ vô hướng của 2 vecto sau a) vecto AC và vecto AF b) vecto DF và vecto EB
Cho hình lập phương ABCD.A’B’C’D’a) Hãy phân tích các vecto
A
C
→
v
à
B
D
→
theo ba vecto
A
B
→
,
A
D
→
,
...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’
a) Hãy phân tích các vecto A C ' → v à B D → theo ba vecto A B → , A D → , A A ' →
b) Tính cos A C ' → , B D → và từ đó suy ra A C ' → v à B D → vuông góc với nhau
Chỉ cần đáp án thôi ạ
Cho hình lập phương ABCD.EFGH. Có bao nhiêu vecto bằng vecto AB có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho?
A. 3
B. 1
C. 6.
D. 7
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto A B → và E G →
A. 90 °
B. 60 °
C. 45 °
D. 120 °
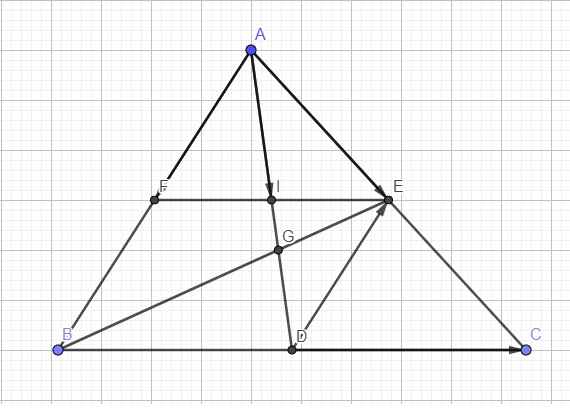
Cho tam giác ABC có trọng tâm G . các điểm D,E,F lần lượt là trung điểm của BC,CA,AB.và I là giao điểm của AD và EF . hãy phân tích các vecto AI,AG,DE,DC theo hai vecto AE ,AF
F là trung điểm AB \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\overrightarrow{AB}\) ; E là trung điểm AC \(\Rightarrow\overrightarrow{AE}=\dfrac{1}{2}\overrightarrow{AC}\)
Ta có EF song song BC (đường trung bình)
Mà D là trung điểm BC \(\Rightarrow\) I là trung điểm EF \(\Rightarrow AI\) là trung tuyến tam giác AEF
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AE}+\dfrac{1}{2}\overrightarrow{AF}\)
Theo tính chất trọng tâm:
\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{2}{3}\left(\overrightarrow{AE}+\overrightarrow{AF}\right)=\dfrac{2}{3}\overrightarrow{AE}+\dfrac{2}{3}\overrightarrow{AF}\)
DE là đường trung bình tam giác ABC
\(\Rightarrow\overrightarrow{DE}=\dfrac{1}{2}\overrightarrow{BA}=-\dfrac{1}{2}\overrightarrow{AB}=-\overrightarrow{AE}\) hay \(\overrightarrow{DE}=-\overrightarrow{AE}+0.\overrightarrow{AF}\)
D là trung điểm BC \(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{DC}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AC}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=-\overrightarrow{AE}+\overrightarrow{AF}\)
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. hãy phân tích vecto AD theo 2 vecto a=AC, b=BD
giúp mình với!
ABCD là hbh \(\Rightarrow\overrightarrow{AD}=\overrightarrow{BC}\)
Ta có:
\(\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{BD}\Rightarrow\overrightarrow{AD}-\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow2\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{BD}\)
\(\Rightarrow\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}=\dfrac{1}{2}\overrightarrow{a}+\dfrac{1}{2}\overrightarrow{b}\)
Đúng 0
Bình luận (0)
Gọi O là giao điểm của AC và BD.
\(\Rightarrow\vec{AD}=\vec{AO}+\vec{OD}=\dfrac{1}{2}\vec{AC}+\dfrac{1}{2}\vec{BD}=\dfrac{1}{2}\vec{a}+\dfrac{1}{2}\vec{b}\)
Đúng 0
Bình luận (0)
Bài 1. Cho tam giác ABC , gọi M là điểm trên cạnh BC sao cho MC = 2MB
1) Phân tích vecto AM theo vecto AB, vecto AC
2) Gọi D là trung điểm của AC, phân tích vecto MD theo vecto BA, vecto BC
3) Gọi E là trung điểm của BD . Chứng minh A, E, M thẳng hàng
4) Phân tích vecto BC theo vecto BD, vecto AM
cho tam giác ABC,M N lần lượt là trung điểm AB và BC. F thuộc AC: AF=2FC, I thuộc EF: 4EI=3FI.Hãy biểu diễn vecto AI theo 2 vecto AE và ÀF