Tính tỉ số của hai đại lượng được cho trong các trường hợp sau:
a) \(\dfrac{3}{4}\) m và 25 cm;
b) 30 phút và \(\dfrac{2}{3}\) giờ;
c) 0,4 kg và 340 g;
d)\(\dfrac{2}{5}\)m và\(\dfrac{3}{4}\)m.
Tính tỉ số của hai đại lượng được cho trong các trường hợp sau:
a) \(\frac{3}{4}m\) và \(25\,cm\); b) \(30\) phút và \(\frac{2}{3}\) giờ.
d) \(0,4\,kg\) và \(340g\) d) \(\frac{2}{5}\,m\) và \(\frac{3}{4}\,m\).
a) Đổi \(25\,cm = \frac{1}{4}\,m\)
Ta có tỉ số của \(\frac{3}{4}m\) và \(25\,cm\) là: \(\frac{3}{4}:\frac{1}{4}=\frac{3}{4}.\frac{4}{1} = 3\)
b) Đổi \(30\) phút = \(\frac{1}{2}\) giờ
Ta có tỉ số của \(30\) phút và \(\frac{2}{3}\) giờ là: \(\frac{1}{2}:\frac{2}{3}=\frac{1}{2}.\frac{3}{2} = \frac{3}{4}\)
c) Đổi \(0,4\,kg = 400\,g\)
Ta có tỉ số của \(0,4\,kg\) và \(340g\) là: \(400:340 = \frac{{400}}{{340}} = \frac{{20}}{{17}}\)
d) Tỉ số của \(\frac{2}{5}\,m\) và \(\frac{3}{4}\,m\) là: \(\frac{2}{5}:\frac{3}{4}=\frac{2}{5}.\frac{4}{3} = \frac{8}{{15}}\)
Tính tỉ số phần trăm của hai số cho trong mỗi trường hợp sau:
a) 3 và 4;
b) −2,66 và 200;
c)\(\dfrac{1}{4}\)và 0,5.
Bài 1.Tìm tỉ số của hai đại lượng trong các trường hợp sau:
a) 4/5m và 72cm c, 0,2 tạ và 40kg
b, 3/10 giờ và 15phút d, 30cm và 7,5 dm
a: 4/5m=80cm
=>Tỉ số là 10:9
b: 3/10 giờ=18 phút
=>Tỉ số là 6/5
c: 0,2 tạ=20kg
=> Tỉ số là 1/2
d: 7,5dm=75cm
=>Tỉ số là 2/5
Các giá trị tương ứng của khối lượng m (g) và thể tích V (cm3) được cho bởi bảng sau:
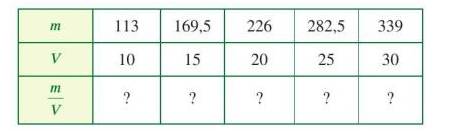
a) Tìm số thích hợp cho 
b) Hai đại lượng m và V có tỉ lệ thuận với nhau không? Vì sao?
c) Xác định hệ số tỉ lệ của m đối với V. Viết công thức tính m theo V
a)
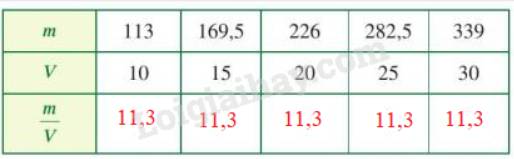
b) Hai đại lượng m và V tỉ lệ thuận với nhau vì tỉ lệ \(\dfrac{m}{V}\) không đổi.
c) Hệ số tỉ lệ của m đối với V là: 11,3
Công thức liên hệ: m = 11,3 . V
Tính tỉ số phần trăm của hai số cho trong mỗi trường hợp sau:
a) 3 và 4;
b) -2,66 và 200;
c) \(\frac{1}{4}\) và 0,5.
a) \(\frac{3}{4} = \left( {\frac{{3.100}}{4}} \right)\% = 75\% \)
b) \(\frac{{ - 2,66}}{{200}} = \left( {\frac{{ - 2,66.100}}{{200}}} \right)\% = - 1,33\% \)
c) \(\frac{{\frac{1}{4}}}{{0,5}} = \left( {\frac{{\frac{1}{4}.100}}{{0,5}}} \right)\% = 50\% \)
Trong các trường hợp sau, hãy kiểm tra xem hai đại lượng m và n có tỉ lệ thuận với nhau hay không.
a)
m | 2 | 4 | 6 | 8 | 10 |
n | 4 | 16 | 36 | 64 | 100 |
b)
m | 1 | 2 | 3 | 4 | 5 |
n | -5 | -10 | -15 | -20 | -25 |
a)
Ta thấy : \(\dfrac{2}{4} \ne \dfrac{4}{{16}} \ne \dfrac{6}{{36}} \ne \dfrac{8}{{64}} \ne \dfrac{{10}}{{100}}\)
Nên m và n không tỉ lệ thuận với nhau.
b)
Ta thấy \(\dfrac{1}{-5} = \dfrac{2}{{-10}} = \dfrac{3}{{-15}}= \dfrac{4}{{-20}} = \dfrac{{5}}{{-25}}\) ( = \( - \dfrac{1}{5}\)) nên m tỉ lệ thuận với n.
Người ta trộn lẫn hai chất lỏng có nhiệt dung riêng, khối lượng, nhiệt độ ban đầu của chúng lần lượt là C1, m1, t1 và C2, t2, m2. Tính tỉ số khối lượng của hai chất lỏng trong các trường hợp sau:
a) Độ biến thiên nhiệt độ của chất lỏng thứ hai gấp đôi so với độ biến thiên nhiệt độ của chất lỏng thứ nhất.
b) Hiệu nhiệt độ ban đầu của hai chất lỏng so với hiệu nhiệt độ cân bằng và nhiệt độ ban đầu của chất lỏng thu nhiệt bằng tỉ số a/b
Hãy tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) trong các trường hợp sau:
a) \(AB = 6cm;CD = 8cm\);
b) \(AB = 1,2m;CD = 42cm\).
a) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{6}{8} = \frac{3}{4}\).
b) Đổi \(1,2m = 120cm\)
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{{120}}{{42}} = \frac{{20}}{7}\).
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.
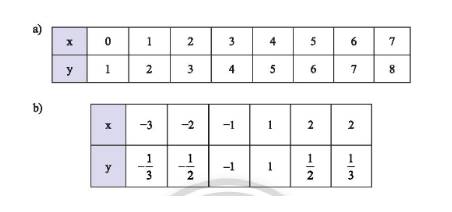
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).