Bài 4: 

b: Xét ΔAHB vuông tại H có HM là đường cao

nên \(AM\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HN là đường cao

nên \(AN\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

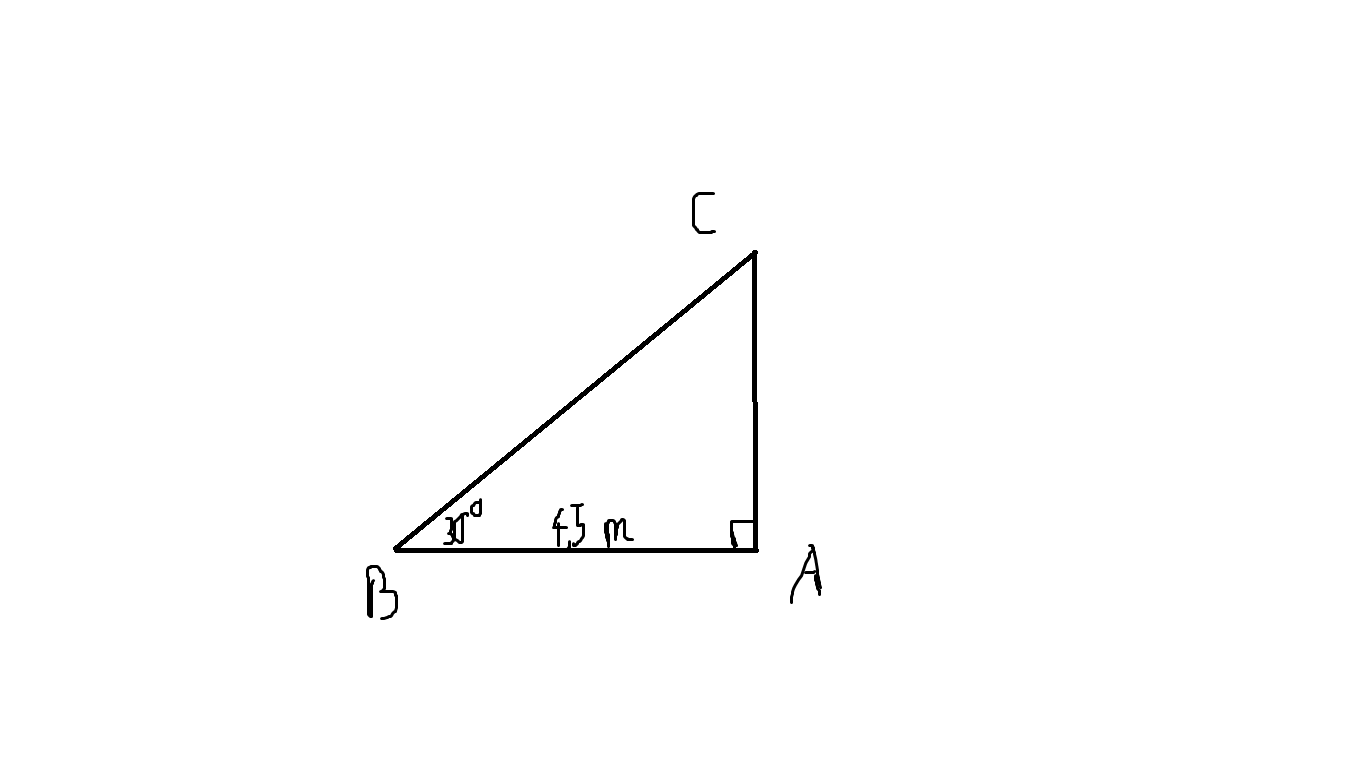
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)

\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)

Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)

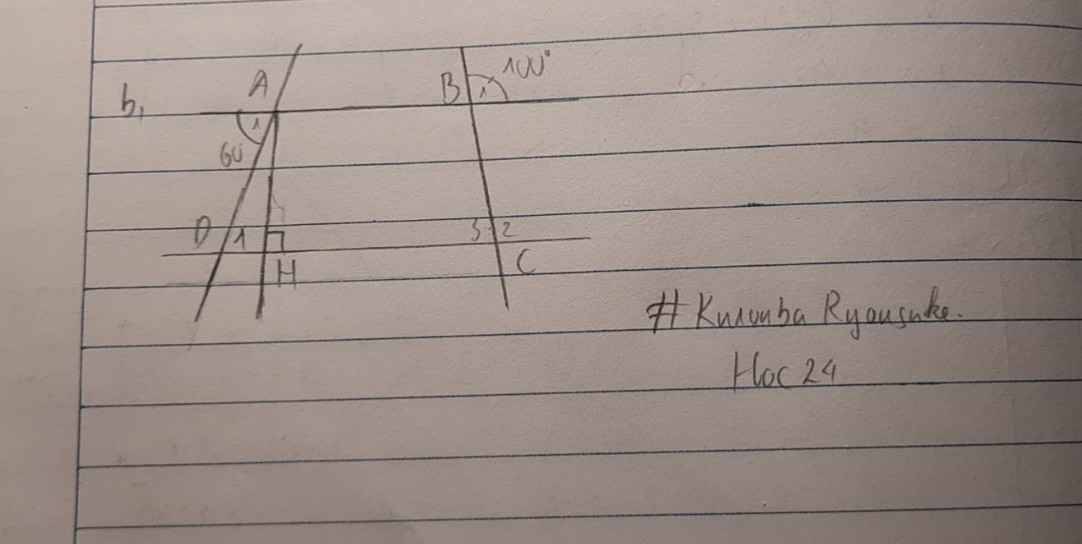
^{*Hình như câu b mình chỉ thấy họ yêu cầu vẽ hình á, k thấy thêm gì nữa bạn ah.}

b) Tách các cặp tính trạng riêng ra :

P:    AaBbDd              x               AaBBDd

->  (Aa x Aa) (Bb x BB) (Dd x Dd)

F1 : KG : (\(\dfrac{1}{4}\)AA : \(\dfrac{2}{4}\) Aa : \(\dfrac{1}{4}\) aa) ( \(\dfrac{1}{2}\) BB :\(\dfrac{1}{2}\) Bb) (\(\dfrac{1}{4}\)DD : \(\dfrac{2}{4}\) Dd : \(\dfrac{1}{4}\) dd )

      KH : (\(\dfrac{3}{4}\)trội : \(\dfrac{1}{4}\) lặn) ( 100% trội ) (\(\dfrac{3}{4}\)trội : \(\dfrac{1}{4}\) lặn)

b1)  Tỉ lệ biến dị tổ hợp ở đời con :

lặn, trội, lặn :  \(\dfrac{1}{4}\) x 1 x \(\dfrac{1}{4}\) = \(\dfrac{1}{16}\)

lặn, trội, trội :   \(\dfrac{1}{4}\) x 1 x \(\dfrac{3}{4}\) = \(\dfrac{3}{16}\)

b2) 

Tỉ lệ 5 gen trội đời con :

AABBDd :   \(\dfrac{1}{4}\) x \(\dfrac{1}{2}\) x \(\dfrac{2}{4}\) = \(\dfrac{1}{16}\)

AaBBDd : \(\dfrac{2}{4}\) x \(\dfrac{1}{2}\) x \(\dfrac{1}{4}\) = \(\dfrac{1}{16}\)

Câu 2: 

Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)

a=1; b=-2m-2; \(c=m^2+4\)

\(\text{Δ}=b^2-4ac\)

\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)

\(=4m^2+8m+4-4m^2-16\)

=8m-12

Để phương trình có hai nghiệm phân biệt thì Δ>0

\(\Leftrightarrow8m>12\)

hay \(m>\dfrac{3}{2}\)

Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)

Vì x1 là nghiệm của phương trình nên ta có: 

\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)

\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)

Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)

\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)

\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)

\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)

\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)

\(\Leftrightarrow m^2+8m-20=0\)

Đến đây bạn tự tìm m là xong rồi

Sai nha bạn

TL: 

Sai nhé bạn 

Bạn k cho mik cái đi nhé 

@@@@@@@@@@@@@@@@@ 

HT

Sai nha

#Bonnie @Ngân Hà

câu 2 phần 2:

\(\left\{{}\begin{matrix}4x+3y=11\\4x-y=7\end{matrix}\right.\)\(< =>\left\{{}\begin{matrix}4y=4\\4x-y=7\end{matrix}\right.< =>\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\).Vậy hệ pt có nghiệm

(x,y)=(2;1)

caau3 phần 2:

\(x^2-2x+m-1=0\)(1)

\(\Delta'=\left(-1\right)^2-\left(m-1\right)=1-m+1=2-m\)

để pt (1) có 2 nghiệm x1,x2<=>\(\Delta'\ge0< =>2-m\ge0< =>m\le2\)

theo vi ét=>\(\left\{{}\begin{matrix}x1+x2=2\left(1\right)\\x1.x2=m-1\left(3\right)\end{matrix}\right.\)

có: \(x1^4\)\(-x1^3=x2^4-x2^3\)

\(< =>x1^4-x2^4-x1^3+x2^3=0\)

\(< =>\left(x1^2-x2^2\right)\left(x1^2+x2^2\right)-\left(x1^3-x2^3\right)\)\(=0\)

\(< =>\left(x1-x2\right)\left(x1+x2\right)\left[\left(x1+x2\right)^2-2x1x2\right]\)\(-\left(x1-x2\right)\left(x1^2+x1x2+x^2\right)=0\)

\(< =>\)\(\left(x1-x2\right)\left[2.2^2-2\left(m-1\right)-\left(x1^2+x1x2+x2^2\right)\right]=0\)

\(< =>.\left(x1-x2\right)\left[8-2m+2-\left(x1+x2\right)^2+x1x2\right]=0\)

<=>\(\left(x1-x2\right)\left[10-2m-4+m-1\right]=0\)

\(< =>\left(x1-x2\right)\left(5-m\right)=0\)

\(=>\left[{}\begin{matrix}x1-x2=0\\5-m=0\end{matrix}\right.< =>\left[{}\begin{matrix}x1=x2\left(2\right)\\m=5\left(loai\right)\end{matrix}\right.\)

thế(2) vào(1)=>\(x1=x2=1\left(4\right)\)

thế (4) vào (3)=>\(m-1=1=>m=2\left(TM\right)\)

vậy m=2 thì....