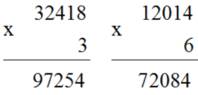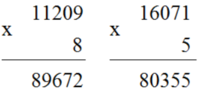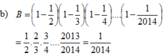Tính: (12014 + 22014 + 32014 + 42014 + 52014) : 5
Những câu hỏi liên quan
Đặt tính rồi tính:
32418 x 3 12014 x 6 11209 x 8 16071 x 5
S = 1 + 3 + 32 + 33 +... + 32014 .Tính tổng
S = 1 + 3 + 32 + 33 +... + 32014
3S = 3 + 32 + 33 + 34 + ... + 32015
3S - S = ( 3 + 32 + 33 + 34 + ... + 32015) - (1 + 3 + 32 + 33 +... + 32014)
2S = 32015 - 1
S = \(\dfrac{3^{2015}-1}{2}\)
Đúng 0
Bình luận (5)
Tính:
B
1
-
1
2
1
-
1
3
1
-
1
4
.
.
.
1
-
1
2014
Đọc tiếp
Tính:
B = 1 - 1 2 1 - 1 3 1 - 1 4 . . . 1 - 1 2014
Tính:
b) B = 1 - 1 2 1 - 1 3 1 - 1 4 . . . 1 - 1 2014
chứng minh: 52014-52013+52012⋮105
Ta có:
A= 52014-52013+52012⋮105
A= 5^2011(5^3- 5^2)+5
A=5^2011(125- 25)+5
A= 5^2011. 105
=> A:105(đpcm)
Đúng 1
Bình luận (0)
5^2014-5^2013+5^2012
=5^2012(5^2-5^1+1)
=5^2012.21 =5^2011.5.21
=5^2011.105
Vậy 5^2014-5^2013+5^2012 chia hết cho 105
chúc bạn học tốt
Đúng 1
Bình luận (0)
Ta có: \(5^{2014}-5^{2013}+5^{2012}\)
\(=5^{2012}\cdot\left(5^2-5+1\right)\)
\(=5^{2011}\cdot5\cdot21\)
\(=5^{2011}\cdot105⋮105\)(đpcm)
Đúng 0
Bình luận (0)
Cho S = 1 - 2 + 22 -23 +...+22012 - 22013 . Tính 3S - 22014
\(S=1-2+2^2-2^3+...+2^{2012}-2^{2013}\)
\(\Rightarrow2S=2-2^2+2^3-2^4+...+2^{2013}-2^{2014}\)
\(\Rightarrow2S+S=2-2^2+2^3-...-2^{2014}+1-2^2-2^3+...-2^{2013}\)
\(\Rightarrow3S=1-2^{2014}\)\(\Rightarrow3S-2^{2014}=1-2^{2015}\)
Đúng 5
Bình luận (0)
Tính giá trị của biểu thức sau :
B=22014-22013-22012-....-23-22-3
Tính giá trị của biểu thức
M
2
2016
C
2017
1
+
2
2014
C
2017
3
+
2
2012
C
2017
5
+
⋯
+
2
0
C
2017
2017
A.
3...
Đọc tiếp
Tính giá trị của biểu thức
M = 2 2016 C 2017 1 + 2 2014 C 2017 3 + 2 2012 C 2017 5 + ⋯ + 2 0 C 2017 2017
A. 3 2017 + 1
B. 1 / 2 3 2017 + 1
C. 3 2017 - 1
D. 1 / 2 3 2017 - 1
Ta có 2 + 1 2017 = C 2017 0 .2 2017 + C 2017 1 .2 2016 + ... + C 2017 2017 .2 0
2 − 1 2017 = C 2017 0 .2 2017 + C 2017 1 .2 2016 . − 1 + ... + C 2017 2017 .2 0 . − 1 2017
Trừ từng vế hai đẳng thức trên ta được:
3 2017 − 1 = 2 C 2017 1 .2 2016 + C 2017 3 .2 2014 + ... + C 2017 2017 .2 0
Vậy M = 3 2017 − 1 2
Chọn đáp án D.
Đúng 0
Bình luận (0)
DẠNG NÂNG CAO:
BÀI 1; TÌM n ∈ N để(3n+1)⋮(n-1)
BÀI 2;THCS Thăng long
cho A=20+21+22+....+22013 và B=22014
Chứng minh rằng A và B là hai số tự nhiên liên tiếp.
Bài 3; Cho A =42+43+44+....+42013+42014
Số B=3A+16 có là số chính phương hay không ? vì sao?
(số chính phương là số bằng bình phương của 1 số tự nhiên)
Bài 4 ; Tính tổng : S=20+21+22+.....+22017
Bài 1:
Ta có: \(3n+1⋮n-1\)
\(\Leftrightarrow3n-3+4⋮n-1\)
mà \(3n-3⋮n-1\)
nên \(4⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(4\right)\)
\(\Leftrightarrow n-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{2;0;3;-1;5;-3\right\}\)(tm)
Vậy: \(n\in\left\{2;0;3;-1;5;-3\right\}\)