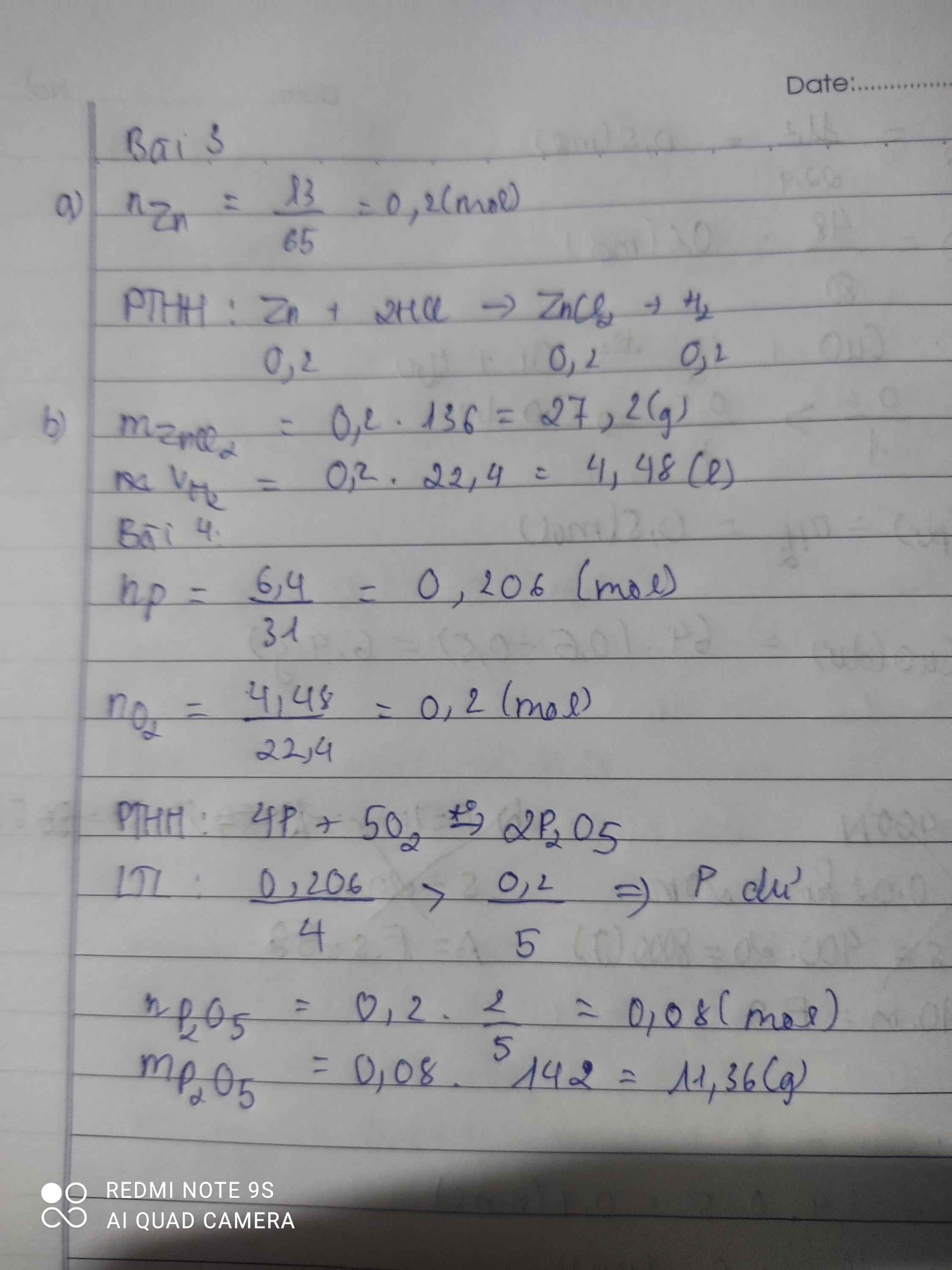giúp mik vs đi ạk 

Những câu hỏi liên quan
.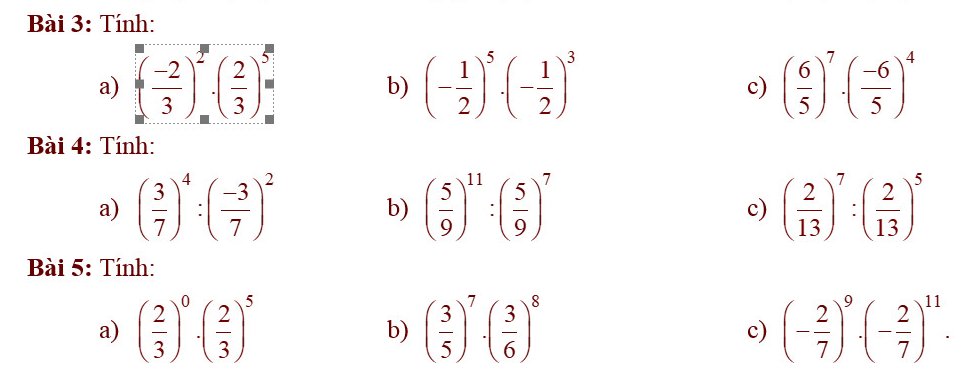
giúp mik vs ạk. mik c.ơn ạ
Bài 3:
a) \(\left(-\dfrac{2}{3}\right)^2\cdot\left(\dfrac{2}{3}\right)^5\)
\(=\left(\dfrac{2}{3}\right)^2\cdot\left(\dfrac{2}{3}\right)^5\)
\(=\left(\dfrac{2}{3}\right)^{2+5}\)
\(=\left(\dfrac{2}{3}\right)^7\)
b) \(\left(-\dfrac{1}{2}\right)^5\cdot\left(-\dfrac{1}{2}\right)^3\)
\(=\left(-\dfrac{1}{2}\right)^{5+3}\)
\(=\left(-\dfrac{1}{2}\right)^8\)
\(=\left(\dfrac{1}{2}\right)^8\)
c) \(\left(\dfrac{6}{5}\right)^7\cdot\left(-\dfrac{6}{5}\right)^4\)
\(=\left(\dfrac{6}{5}\right)^7\cdot\left(\dfrac{6}{5}\right)^4\)
\(=\left(\dfrac{6}{5}\right)^{7+4}\)
\(=\left(\dfrac{6}{5}\right)^{11}\)
Đúng 1
Bình luận (0)
Bài 4:
a) \(\left(\dfrac{3}{7}\right)^4:\left(-\dfrac{3}{7}\right)^2\)
\(=\left(\dfrac{3}{7}\right)^4\cdot\left(\dfrac{3}{7}\right)^2\)
\(=\left(\dfrac{3}{7}\right)^{4+2}\)
\(=\left(\dfrac{3}{7}\right)^6\)
b) \(\left(\dfrac{5}{9}\right)^{11}:\left(\dfrac{5}{9}\right)^7\)
\(=\left(\dfrac{5}{9}\right)^{11-7}\)
\(=\left(\dfrac{5}{9}\right)^4\)
c) \(\left(\dfrac{2}{13}\right)^7:\left(\dfrac{2}{13}\right)^5\)
\(=\left(\dfrac{2}{13}\right)^{7-5}\)
\(=\left(\dfrac{2}{13}\right)^2\)
Đúng 2
Bình luận (0)
Bài 5:
a) \(\left(\dfrac{2}{3}\right)^0\cdot\left(\dfrac{2}{3}\right)^5\)
\(=1\cdot\left(\dfrac{2}{3}\right)^5\)
\(=\left(\dfrac{2}{3}\right)^5\)
b) \(\left(\dfrac{3}{5}\right)^7\cdot\left(\dfrac{3}{5}\right)^8\)
\(=\left(\dfrac{3}{5}\right)^{7+8}\)
\(=\left(\dfrac{3}{5}\right)^{15}\)
c) \(\left(-\dfrac{2}{7}\right)^9\cdot\left(-\dfrac{2}{7}\right)^{11}\)
\(=\left(-\dfrac{2}{7}\right)^{9+11}\)
\(=\left(-\dfrac{2}{7}\right)^{20}\)
Đúng 0
Bình luận (0)
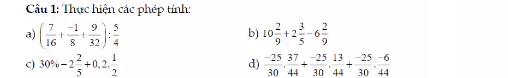 giúp mik vs ạk, mik cần gấp
giúp mik vs ạk, mik cần gấp
Giúp mik vs ạk 
a) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=4^2+3^2.\\ \Leftrightarrow BC^2=25.\\\Leftrightarrow BC=5\left(BC>0\right). \)
b) Xét \(\Delta ABD\) và \(\Delta ABC\):
AD = AC (gt).
\(\widehat{DAB}=\widehat{CAB}\left(=90^o\right).\)
AD chung.
\(\Rightarrow\Delta ABD=\Delta ABC\left(c-g-c\right).\)
\(\Rightarrow\widehat{ADB}=\widehat{ACB}\) (2 góc tương ứng).
\(\Rightarrow\Delta BDC\) cân tại B.
Đúng 1
Bình luận (0)
giúp mik vs ạk
a) Ta có: BC+CN=BN(C nằm giữa B và N)
CB+BM=CM(B nằm giữa C và M)
mà BM=CN(gt)
nên BN=CM
Xét ΔABN và ΔACM có
AB=AC(ΔABC cân tại A)
\(\widehat{ABN}=\widehat{ACM}\)(hai góc ở đáy của ΔABC cân tại A)
BN=CM(cmt)
Do đó: ΔABN=ΔACM(c-g-c)
b) Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
c) Ta có: ΔABM=ΔACN(cmt)
nên \(\widehat{AMB}=\widehat{ANC}\)(hai góc tương ứng)
hay \(\widehat{HMB}=\widehat{KNC}\)
Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN(gt)
\(\widehat{HMB}=\widehat{KNC}\)(cmt)
Do đó: ΔHBM=ΔKCN(cạnh huyền-góc nhọn)
Suy ra: HB=KC(hai cạnh tương ứng)
d) Ta có: ΔABM=ΔACN(cmt)
nên AM=AN(hai cạnh tương ứng)
Ta có: AH+HM=AM(H nằm giữa A và M)
AK+KB=AN(K nằm giữa A và N)
mà AM=AN(cmt)
và HM=KB(cmt)
nên AH=AK
Xét ΔAHK có AH=AK(cmt)
nên ΔAHK cân tại A(Định nghĩa tam giác cân)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
Ta có: ΔAHK cân tại A(cmt)
nên \(\widehat{AHK}=\dfrac{180^0-\widehat{HAK}}{2}\)(Số đo của một góc ở đáy trong ΔAHK cân tại A)
hay \(\widehat{AHK}=\dfrac{180^0-\widehat{MAN}}{2}\)(1)
Ta có: ΔAMN cân tại A(cmt)
nên \(\widehat{AMN}=\dfrac{180^0-\widehat{MAN}}{2}\)(Số đo của một góc ở đáy trong ΔAMN cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AHK}=\widehat{AMN}\)
mà \(\widehat{AHK}\) và \(\widehat{AMN}\) là hai góc ở vị trí đồng vị
nên HK//MN(Dấu hiệu nhận biết hai đường thẳng song song)
hay HK//BC(Đpcm)
e) Ta có: ΔHBM=ΔKCN(cmt)
nên \(\widehat{HBM}=\widehat{KCN}\)(hai góc tương ứng)
mà \(\widehat{HBM}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCN}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)
Xét ΔAHK có AH=AK(cmt)
nên ΔAHK cân tại A(Định nghĩa tam giác cân)
f) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(ΔOBC cân tại O)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy AO là đường trung trực của BC
hay AO\(\perp\)BC(Đpcm)
Đúng 1
Bình luận (0)
Tính biểu thức sau:
0,35 x 16 : 0,28 - ( 2,34 + 1,17 : 4,5 ) : 0,25
giúp mik giải toán này nhanh vs ạk mik cần ấp ạk
`0,35xx16:0,28-(2,34+1,17:4,5):0,25`
`=5,6:0,28-(2,34+0,26):0,25`
`=20-2,6:0,25`
`=20-10,4=9,6`
Đúng 0
Bình luận (0)
Giúp mik bài 5-6 vs ạk
Mik sẽ vote 5sao 
Giải giúp mik vs ạk
Cảm ơn 
28 I haven't gone to HCM City for 2 years
29 We have lived in My Tho for ten years
30 Lan didn't go to school last week
31 He was at home yesterday
Đúng 2
Bình luận (0)
Question8:
29. We live in Phu Tho about ten years.
30. I will see him tomorrow.
31. Lan didn't go to school last week
32. He was at home yesterday.
Đúng 0
Bình luận (0)
giúp mik câu J bài 1 vs ạk![]() cảm ơn ạk
cảm ơn ạk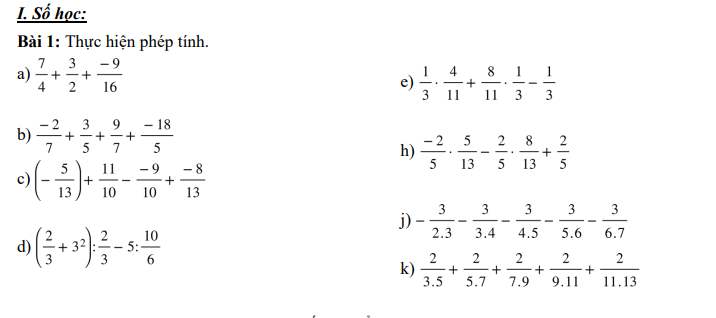
a) 7/4 + 3/2 + ( - 9/16 ) = 13/4 + ( -9/16 ) = 41/112
b) - 2/7 + 3/5 + 9/7 + ( -18/5 )= ( - 2/7 + 9/7 ) + [( 3/5 + ( - 18/5 )] = 1 + ( - 3/1 ) = - 2/1
< tách ra ik >
Đúng 2
Bình luận (0)
a) 7/4 + 3/2 + ( - 9/16 ) = 13/4 + ( -9/16 ) = 41/112
b) - 2/7 + 3/5 + 9/7 + ( -18/5 )= ( - 2/7 + 9/7 ) + [( 3/5 + ( - 18/5 )] = 1 + ( - 3/1 ) = - 2/1
< tách ra ik >
Đúng 1
Bình luận (0)
Giúp mik bài 4 nhanh vs ạk, cảm ơn ae nhìu😁
4P+5O2-to>2P2O5
0,2-------0,08 mol
n P=\(\dfrac{6,4}{31}\)=\(\dfrac{32}{155}\) mol
n O2=\(\dfrac{4,48}{22,4}=0,2mol\)
=>P dư
m P dư =\(\dfrac{9}{775}\).31=0,36g
=>m P2O5= 0,08.142=11,36g
Đúng 1
Bình luận (0)