Thầy Nguyễn Việt Lâm giúp em với ạ
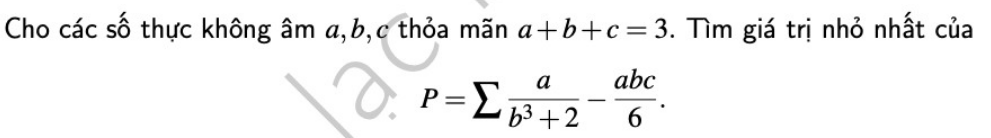
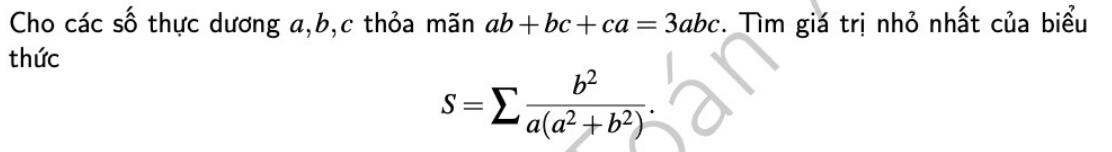
thầy nguyễn việt lâm giúp em với ạ

5.
\(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ac}+\sqrt{ab}\)
\(\Rightarrow\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\dfrac{a}{a+\sqrt{ac}+\sqrt{ab}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự:
\(\dfrac{b}{b+\sqrt{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\dfrac{c}{c+\sqrt{\left(a+c\right)\left(b+c\right)}}\le\dfrac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng vế với vế:
\(P\le\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1\)
Dấu "=" xảy ra khi \(a=b=c\)
6.
\(P=\dfrac{a}{1+b-a}+\dfrac{b}{1+c-b}+\dfrac{c}{1+a-c}\)
Thay \(1=a+b+c\)
\(\Rightarrow P=\dfrac{a}{2b+c}+\dfrac{b}{2c+a}+\dfrac{c}{2a+b}\)
\(P=\dfrac{a^2}{2ab+ac}+\dfrac{b^2}{2bc+ab}+\dfrac{c^2}{2ac+bc}\)
\(P\ge\dfrac{\left(a+b+c\right)^2}{3ab+3bc+3ca}\ge\dfrac{3\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}=1\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
7.
\(T=\left(x^2\right)^2+\left(y^2\right)^2+\left(z^2\right)^2\ge\dfrac{1}{3}\left(x^2+y^2+z^2\right)^2\)
\(T\ge\dfrac{1}{3}\left(xy+yz+zx\right)^2=\dfrac{1}{3}\)
\(T_{min}=\dfrac{1}{3}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)
Thầy Nguyễn Việt Lâm ơi giúp em mấy bài này với.Em sắp phải nộp rồi ạ 

4.
\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)
\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
5.
Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
Đặt vế trái là P
\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)
Quay lại dòng 3 của bài số 4
6.
Do a;b;c không âm, ta có:
\(b^2\left(b-1\right)^2\left(b+2\right)\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2-6\ge-6\)
\(\Leftrightarrow-\left(3-b^2\right)\left(b^3+2\right)\ge-6\)
\(\Leftrightarrow6\ge\left(3-b^2\right)\left(b^3+2\right)\)
\(\Rightarrow\dfrac{1}{b^3+2}\ge\dfrac{3-b^2}{6}\)
\(\Rightarrow\dfrac{a}{b^3+2}\ge\dfrac{a\left(3-b^2\right)}{6}\)
Tương tự: \(\dfrac{b}{c^3+2}\ge\dfrac{b\left(3-c^2\right)}{6}\) ; \(\dfrac{c}{a^3+2}\ge\dfrac{c\left(3-a^2\right)}{6}\)
Cộng vế: \(P\ge\dfrac{a+b+c}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}=\dfrac{3}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}\)
Không mất tính tổng quát, giả sử \(b=mid\left\{a;b;c\right\}\)
\(\left(b-a\right)\left(b-c\right)\le0\)
\(\Leftrightarrow b^2+ac\le ab+bc\)
\(\Leftrightarrow ab^2+ca^2\le a^2b+abc\)
\(\Rightarrow ab^2+bc^2+ca^2+abc\le bc^2+a^2b+2abc=b\left(a+c\right)^2=4b\left(\dfrac{a+c}{2}\right)\left(\dfrac{a+c}{2}\right)\le\dfrac{4}{27}\left(a+b+c\right)^3=4\)
\(\Rightarrow P\ge\dfrac{3}{2}-\dfrac{4}{6}=\dfrac{5}{6}\)
Có ai có facebook thầy Nguyễn Việt Lâm ko ạ cho mình xin với=))
Mọi người ơi giúp em với em ko làm dc mấy bài này mà trước đêm nay em phải nộp rồi ( thầy nguyễn việt lâm giúp em với)
bài1:Gọi x, y là các số thực sao cho 4x2+9y2=13.Chứng minh bất đẳng thức-13/6≤x+y≤13
bài2:Gọi x, y là các số thực sao cho: 36x2+16y2=9.Chứng minh bất đẳng thức |y-2x|≤ 5/4
bài3:Gọi x là các số thực sao cho 1≤x≤3.tìm GTLN và GTNN giá trị của B=6\(\sqrt{x-1}\)+8\(\sqrt{3-x}\)
bài4:gọi a,b là các số thực sao cho 3a+4b=7.Chứng minh bất đẳng thức 3a2+4b2 >=7
bài5:gọi x,y là các số thực sao cho 36x2+16y2=9.Tìm GTLN và GTNN của C=y-2x+5
1.
\(\left(x+y\right)^2=\left(\dfrac{1}{2}.2x+\dfrac{1}{3}.3y\right)^2\le\left(\dfrac{1}{4}+\dfrac{1}{9}\right)\left(4x^2+9y^2\right)=\dfrac{169}{36}\)
\(\Rightarrow-\dfrac{13}{6}\le x+y\le\dfrac{13}{6}\)
Dấu "=" lần lượt xảy ra tại \(\left(-\dfrac{3}{2};-\dfrac{2}{3}\right)\) và \(\left(\dfrac{3}{2};\dfrac{2}{3}\right)\)
2.
\(\left(y-2x\right)^2=\left(\dfrac{1}{4}.4y+\left(-\dfrac{1}{3}\right).6x\right)^2\le\left(\dfrac{1}{16}+\dfrac{1}{9}\right)\left(16y^2+36x^2\right)=\dfrac{25}{16}\)
\(\Rightarrow\left|y-2x\right|\le\dfrac{5}{4}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\mp\dfrac{2}{5};\pm\dfrac{9}{20}\right)\)
3.
\(B^2=\left(6.\sqrt{x-1}+8\sqrt{3-x}\right)^2\le\left(6^2+8^2\right)\left(x-1+3-x\right)=200\)
\(\Rightarrow B\le2\sqrt{10}\)
Dấu "=" xảy ra khi \(\dfrac{\sqrt{x-1}}{6}=\dfrac{\sqrt{3-x}}{8}\Leftrightarrow x=\dfrac{43}{25}\)
\(B=6\sqrt{x-1}+6\sqrt{3-x}+2\sqrt{3-x}\ge6\sqrt{x-1}+6\sqrt{3-x}\)
\(B\ge6\left(\sqrt{x-1}+\sqrt{3-x}\right)\ge6\sqrt{x-1+3-x}=6\sqrt{2}\)
\(B_{min}=6\sqrt{2}\) khi \(\sqrt{3-x}=0\Rightarrow x=3\)
4.
\(49=\left(3a+4b\right)^2=\left(\sqrt{3}.\sqrt{3}a+2.2b\right)^2\le\left(3+4\right)\left(3a^2+4b^2\right)\)
\(\Rightarrow3a^2+4b^2\ge\dfrac{49}{7}=7\)
Dấu "=" xảy ra khi \(a=b=1\)
5.
\(\left(y-2x\right)^2=\left(\dfrac{1}{4}.4y-\dfrac{1}{3}.6x\right)^2\le\left(\dfrac{1}{16}+\dfrac{1}{9}\right)\left(16y^2+36x^2\right)=\dfrac{25}{16}\)
\(\Rightarrow-\dfrac{5}{4}\le y-2x\le\dfrac{5}{4}\)
\(\Rightarrow-\dfrac{5}{4}+5\le y-2x+5\le\dfrac{5}{4}+5\)
\(\Rightarrow\dfrac{15}{4}\le y-2x+5\le\dfrac{25}{4}\)
\(C_{min}=\dfrac{15}{4}\) khi \(\left(x;y\right)=\left(\dfrac{2}{5};-\dfrac{9}{20}\right)\)
\(C_{max}=\dfrac{25}{4}\) khi \(\left(x;y\right)=\left(-\dfrac{2}{5};\dfrac{9}{20}\right)\)
Lần sau lưu ý đăng câu hỏi 1 lần thôi, em đăng nhiều lần lặp lại sẽ bị xóa + ko ai giải cho đâu

Làm hộ em câu 9 bài hình thôi ạ Nguyễn Việt Lâm Giáo viên
(O) và (D) cắt nhau tại A và M \(\Rightarrow AM\perp OD\)
\(\Rightarrow\widehat{AOD}=\widehat{ABN}\) (cùng phụ \(\widehat{BAM}\))
\(\Rightarrow OD||BN\) (góc đồng vị bằng nhau)
\(\Rightarrow OBND\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow OB=DN\), mà \(\left\{{}\begin{matrix}AB=DC\\OB=\dfrac{1}{2}AB\end{matrix}\right.\) \(\Rightarrow OB=\dfrac{1}{2}CD\Rightarrow DN=\dfrac{1}{2}DC\Rightarrow N\) là trung điểm CD

cho các số dương x y z thỏa mãn x+y+z=2
Tìm min P = \(\dfrac{x^2}{y+z}\)+\(\dfrac{y^2}{z+x}\)+\(\dfrac{z^2}{x+y}\)
Thầy Lâm giúp với em với ạ
Lời giải:
Áp dụng BĐT AM-GM:
$\frac{x^2}{y+z}+\frac{y+z}{4}\geq 2\sqrt{\frac{x^2}{y+z}.\frac{y+z}{4}}=x$
$\frac{y^2}{x+z}+\frac{x+z}{4}\geq y$
$\frac{z^2}{x+y}+\frac{x+y}{4}\geq z$
Cộng theo vế các BĐT trên và thu gọn ta được:
$P\geq \frac{x+y+z}{2}=\frac{2}{2}=1$
Vậy $P_{\min}=1$ khi $x=y=z=\frac{2}{3}$
Cô thầy giúp em xác định yếu tố tự sự và miêu tả trong bài. Mẹ và quả của Nguyễn Khoa Điềm với ạ
E hoir giúp c của e, nhờ thầy Lâm trả lời giúp e ạ 
\(log_x\left(x^2y^3\right)=log_xx^2+log_xy^3=2+3log_xy\)
\(\Rightarrow2+3log_xy=1\Rightarrow log_xy=-\dfrac{1}{3}\)
\(N=\dfrac{log_x\left(x^2y^3\right)}{log_x\left(\dfrac{\sqrt[5]{x^3y^2}}{xy^3}\right)}=\dfrac{1}{log_x\left(\sqrt[5]{x^3y^2}\right)-log_xxy^3}=\dfrac{1}{log_x\sqrt[5]{x^3}+log_x\sqrt[5]{y^2}-\left(log_xx+log_xy^3\right)}\)
\(=\dfrac{1}{\dfrac{3}{5}+\dfrac{2}{5}log_xy-\left(1+3log_xy\right)}=\dfrac{1}{\dfrac{3}{5}+\dfrac{2}{5}.\left(-\dfrac{1}{3}\right)-1-3.\left(-\dfrac{1}{3}\right)}=\dfrac{15}{7}\)
thưa các thầy , cô trên hoc24 ,em bị mất tài khoản trên oline math rồi ạ . Em là tiểu thư họ nguyễn nhờ các thầy cô giúp em tìm lại nick ạ ![]()
Uừm chắc tại cậu hay hỏi nhưng câu hoi như là: 1+1 hay là cậu trả lời linh tinh như là thiếu dề rôi chẳng hạn...bị 1 lần thì chắc ko sao nhưng nếu mà lặp lại nhiều lần thì online math sẽ xóa tài khoản luôn đấy!