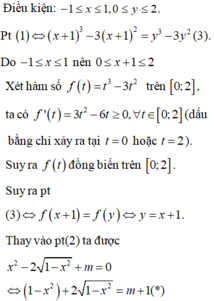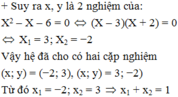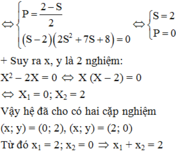Tìm nghiệm nguyên dương của phương trình:x3-y3=95(x2+y2)

Những câu hỏi liên quan
Tìm các số nguyên dương thỏa mãn x3 - y3 = 133(x2 + y2)
Tìm tất cả các nghiệm nguyên của phương trình:
x.(x2 + 2x + 4) = y3 - 3
*Sử dụng phương pháp chặn (hai đầu):
\(x\left(x^2+2x+4\right)=y^3-3\left(1\right)\)
\(\Leftrightarrow2x^2+4x+3=y^3-x^3\)
Ta có \(2x^2+4x+3=2\left(x+1\right)^2+1>0\)
\(\Rightarrow y^3-x^3>0\Rightarrow y^3>x^3\left(2\right)\)
Lại có: \(\left(x+2\right)^3-y^3=\left(x^3+6x^2+12x+8\right)-\left(x^3+2x^2+4x+3\right)=4x^2+8x+5=4\left(x+1\right)^2+1>0\)
\(\Rightarrow y^3< \left(x+2\right)^3\left(3\right)\)
Từ (2), (3) suy ra \(x^3< y^3< \left(x+2\right)^3\Rightarrow y^3=\left(x+1\right)^3\).
Thay vào (1) ta được:
\(x^3+2x^2+4x=\left(x+1\right)^3-3\)
\(\Leftrightarrow x^3+2x^2+4x=x^3+3x^2+3x+1-3\)
\(\Leftrightarrow x^2-x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Với \(x=2\Rightarrow y=3\)
Với \(x=-1\Rightarrow y=0\)
Vậy các nghiệm nguyên của pt (1) là \(\left(x;y\right)=\left(2;3\right),\left(-1;0\right)\)
Đúng 2
Bình luận (0)
Tìm nghiệm nguyên dương của hệ phương trình:
x
+
y
z
x
3
+
y
3
z
2
Đọc tiếp
Tìm nghiệm nguyên dương của hệ phương trình: x + y = z x 3 + y 3 = z 2
Ta có: x 3 + y 3 = ( x + y ) 2 < = > ( x + y ) ( x 2 − x y + y 2 − x − y ) = 0
Vì x, y nguyên dương nên x+y > 0, ta có: x 2 − x y + y 2 − x − y = 0
⇔ 2 ( x 2 − x y + y 2 − x − y ) = 0 ⇔ x - y 2 + x - 1 2 + ( y - 1 ) 2 = 2
Vì x, y nguyên nên có 3 trường hợp:
+ Trường hợp 1: x − y = 0 x - 1 2 = 1 ⇔ x = y = 2 , z = 4 y - 1 2 = 1
+ Trường hợp 2: x − 1 = 0 x - y 2 = 1 ⇔ x = 1 , y = 2 , z = 3 y - 1 2 = 1
+ Trường hợp 3: y − 1 = 0 x - y 2 = 1 x - 1 2 = 1 ⇔ x = 2 , y = 1 , z = 3
Vậy hệ có 3 nghiệm (1,2,3);(2,1,3);(2,2,4)
Đúng 0
Bình luận (0)
Hỏi có bao nhiêu giá trị nguyên của m để hệ phương trình sau có nghiệm:
x
3
-
y
3
+
3
y
2
-
3
x
-
2...
Đọc tiếp
Hỏi có bao nhiêu giá trị nguyên của m để hệ phương trình sau có nghiệm:
x 3 - y 3 + 3 y 2 - 3 x - 2 = 0 1 x 2 + 1 - x 2 - 3 2 y - y 2 + m = 0 2
A. 1
B. 3
C. 2
D. 4
Tìm nghiệm nguyên của phương trình: x4+x2+1=y2
Ta có x4 + x2 + 1 = y2
Lại có x4 + 2x2 + 1 ≥ x4 + x2 + 1 hay (x2 + 1)2 ≥ x4 + x2 + 1
=> (x2 + 1)2 ≥ y2 (1)
Lại có x4 + x2 + 1 > x4 => y2 > x4 (2)
Từ (1) và (2), ta có x4 < y2 ≤ (x2 + 1)2
<=> y2 = (x2 + 1)2 = x4 + 2x2 + 1
Mà x4 + x2 + 1 = y2 => x4 + 2x2 + 1 = x4 + x2 + 1
<=> x2 = 0 <=> x = 0
Thay vào, ta có 1 = y2 <=> y ∈ {-1,1}
Vậy ...
Đúng 0
Bình luận (0)
Biết hệ phương trình
x
3
+
y
3
19
x
+
y
8
+...
Đọc tiếp
Biết hệ phương trình x 3 + y 3 = 19 x + y 8 + x y = 2 có hai nghiệm ( x 1 ; y 1 ) ; ( x 2 ; y 2 ) . Tổng x 1 + x 2 bằng?
A. −1
B. 2
C. 1
D. 0
Biết hệ phương trình
x
3
+
y
3
8
x
+
y
+
2
x
y...
Đọc tiếp
Biết hệ phương trình x 3 + y 3 = 8 x + y + 2 x y = 2 có hai nghiệm ( x 1 ; y 1 ) ; ( x 2 ; y 2 ) . Tổng x 1 + x 2 bằng?
A. 2
B. −2
C. 1
D. 0
tìm nghiệm nguyên dương của phương trình x^3 - y^ = 95(x^2 + y^2)
Tìm nghiệm nguyên của phương trình : x2 - xy +y2 = x-y
<=>x^2+y^2-x-y-xy=0
<=>2x^2+2y^2-2x-2y-2xy=0
<=>(x-y)^2+(x-1)^2+(y-1)^2=2
mà 2=0+1+1=1+0+1=1+1+0
(phần này tách số 2 ra thành tổng 3 số chính phương)
Xét trường hợp 1:
(x-y)^2=0
(x-1)^2=1
(y-1)^2=1
Giải ra ta được x=2, y=2
Tương tự xét các trường hợp còn lại.
Kết quả: 5 nghiệm: (2;2) ; (1;0) ; (1;2) ; (0;1) ; (2;1)
Đúng 0
Bình luận (0)
x2 - xy + y2 = x - y
<=> x2 - xy + y2 - x + y = 0
<=> x ( x - y) + y2 - ( x - y) = 0
<=> (x-1)(x-y)y2 =0
Đúng 0
Bình luận (0)
Tìm các nghiệm nguyên của phương trình sau: 7(x2+y2) = 25(x+y)