a) cos2 (α +x) +cos22 x - 2 cosα cosx.cos(α +x);
b) sin4x.sin10x-sin11x.sin3x-sin7x.sinx
Những câu hỏi liên quan
- Mn ơi, help me!
Chứng minh rằng giá trị của mỗi biểu thức sau không phụ thuộc vào x
a) cos2(α +x)+cos2x-2cosα cosx.cos(α +x);
b) sin4x.sin10x-sin11x.sin3x-sin7x.sinx
TL:
Bạn tham khảo cái link này nha https://vietjack.com/giai-toan-10-nang-cao/bai-49-trang-215-sgk-dai-so-10-nang-cao.jsp
~ t.i.c.k cho mk nha , học tốt ~
Đúng 0
Bình luận (0)
Tính
c
o
s
2
(
α
+
x
)
+
c
o
s
2
x
-
2
cos
α
.
c
o
s
x
.
c
o
s
(
α
+
x
)
A.
1
2
(
1
-
cos...
Đọc tiếp
Tính c o s 2 ( α + x ) + c o s 2 x - 2 cos α . c o s x . c o s ( α + x )
A. 1 2 ( 1 - cos 2 α )
B. c o s 2 α
C. ( 1 - cos 2 α )
D. sin α
CMR: α<45* ta có công thức:
a/ \(sin^2\alpha=\frac{1-cos2\text{α}}{2}\)
b/ \(cos^2\text{α}=\frac{1+cos2\text{α}}{2}\)
c/ \(cos2\text{α}=cos^2\text{α}-sin^2\text{α}\)
Rút gọn bt
a/A=(sinα +cosα )2 +(sinα-cosα)2
b/ B=(1+tan2α ) (1-sin2α) -(1+cot2α)(1-cos2α)
a/ \(A=\left(sin\alpha+cos\alpha\right)^2+\left(sin\alpha-cos\alpha\right)^2=2\left(sin^2\alpha+cos^2\alpha\right)=2\)
b/ \(B=\left(1+tan^2\alpha\right)\left(1-sin^2\alpha\right)-\left(1+cotg^2\alpha\right)\left(1-cos^2\alpha\right)\)
\(=\left(1+\frac{sin^2\alpha}{cos^2\alpha}\right)\left(1-sin^2\alpha\right)-\left(1+\frac{cos^2\alpha}{sin^2\alpha}\right)\left(1-cos^2\alpha\right)\)
\(=\frac{1}{cos^2\alpha}.cos^2\alpha-\frac{1}{sin^2\alpha}.sin^2\alpha=1-1=0\)
Đúng 0
Bình luận (0)
A = \(\dfrac{\text{sinα + cosα}}{\text{sinα - cosα}}\) Tính α biết tan α = \(\sqrt{3}\)
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{tana+1}{tana-1}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}\)
Đúng 1
Bình luận (0)
21 tháng 10 2021 lúc 21:30
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
Chứng minh các biểu thức sau không phụ thuộc vào α
A=(sinα+cosα)2+(sinα−cosα)2
B=sin4α(1+2cos2α)+cos4α(1+2sin2α)
C=sin4α(3−2sin2α)+cos4α(3−2cos2α)
Giúp tớ điii
\(A=\left(\sin\alpha+\cos\alpha+\sin\alpha-\cos\alpha\right)^2-2\left(\sin\alpha+\cos\alpha\right)\left(\sin\alpha-\cos\alpha\right)\)
\(=4\sin^2\alpha-2\sin^2\alpha+2\cos^2\alpha=2\left(\sin^2\alpha+\cos^2\alpha\right)=2\)
\(B=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2-1=0\)
\(C=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\)
\(=3\left(\sin^2\alpha+\cos^2\alpha-\frac{1}{9}\right)^2-\frac{1}{9}=\frac{61}{27}\)
Đúng 0
Bình luận (0)
Cho góc
α
thỏa mãn:
π
α
3
π
2
và
A
sin
2
α
+
cos
α
+
π
2
Đọc tiếp
Cho góc α thỏa mãn: π < α < 3 π 2 và A = sin 2 α + cos α + π 2
Cho góc
α
thỏa mãn
π
α
3
π
2
và
tan
α
2
: Tính giá trị của biểu thức
A
sin
2
α
+
cos
α
+
π
2
A.
4
+
2
5
10...
Đọc tiếp
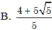
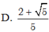
Cho góc α thỏa mãn π < α < 3 π 2 và tan α = 2 : Tính giá trị của biểu thức A = sin 2 α + cos α + π 2
A. 4 + 2 5 10
B. 4 + 5 5 5
C. 4 + 2 5 5
D. 2 + 5 5
