Cho △ABC vuông tại A , kẻ đường cao AH . Trên cạnh AC lấy điểm K sao cho AK = AH . Kẻ KD vuông góc với AC
a, C/m △AHD = △AKD
b,C/m △AED cân
Cho △ABC vuông tại A , kẻ đường cao AH . Trên cạnh AC lấy điểm K sao cho AK = AH . Kẻ KD vuông góc với AC
a, C/m △AHD = △AKD
b,C/m AD là đường trung trực của doạn thẳng HK
a) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
AH=AK(gt)
Do đó: ΔAHD=ΔAKD(Cạnh huyền-cạnh góc vuông)
a) Xét tam giác AHDAHD và AKDAKD có:
ˆAHD=ˆAKD=900AHD^=AKD^=900
ADAD chung
AH=AKAH=AK (gt)
⇒△AHD=△AKD⇒△AHD=△AKD (ch-cgv)
b)
Vì △AHD=△AKD△AHD=△AKD nên DH=DKDH=DK
Mà AH=AKAH=AK
Kết hợp 2 điều này lại suy ra ADAD là trung trực của HK
Cho △ABC vuông tại A , kẻ đường cao AH . Trên cạnh AC lấy điểm K sao cho AK = AH . Kẻ KD vuông góc với AC
a, C/m △AHD = △AKD
b,C/m AD là đường trung trực của doạn thẳng HK
Lời giải:
a) Xét tam giác $AHD$ và $AKD$ có:
$\widehat{AHD}=\widehat{AKD}=90^0$
$AD$ chung
$AH=AK$ (gt)
$\Rightarrow \triangle AHD=\triangle AKD$ (ch-cgv)
b)
Vì $\triangle AHD=\triangle AKD$ nên $DH=DK$
Mà $AH=AK$
Kết hợp 2 điều này lại suy ra $AD$ là trung trực của $HK$
Ta có đpcm.
Cho tam giác ABC vuông tại A , kẻ đường cao AH . trên cạnh AC lấy điểm K sao cho AK = AH . kẻ KD vuông góc với AC tại K ( D thuộc BC ) > chứng minh
a, tam giác AHD = tam giác AKD
b, AD là đường trung trực của đoạn thẳng AK
a: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AH=AK
AD chung
=>ΔAHD=ΔAKD
b: AK=AH
DH=DK
=>AD là trung trực của HK
Cho ΔABC vuông tại A, kẻ đường cao AH. Trên cạnh AC lấy điểm
K sao cho AK = AH. Kẻ KD⊥AC (DϵBC). Chứng minh:
a) AHD = AKD
b) AD là đường trung trực của đoạn thẳng HK
c) AD là tia phân giác của góc HAK
a) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
AH=AK(gt)
Do đó: ΔAHD=ΔAKD(cạnh huyền-cạnh góc vuông)
b) Vì △AHD=△AKD nên DH=DK
Mà AH=AK
Kết hợp 2 điều này lại suy ra AD là trung trực của HK
Ta có đpcm
c) Ta có: ΔAHD=ΔAKD(cmt)
nên \(\widehat{HAD}=\widehat{KAD}\)(hai góc tương ứng)
mà tia AD nằm giữa hai tia AH,AK
nên AD là tia phân giác của \(\widehat{HAK}\)(Đpcm)
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Trên cạnh AC lấy điểm K sao cho AK=AH. Kẻ KD vuông góc với AC. Chọn câu đúng
A. Tam giác AHD= tam giác AKD
B. AD là đường trung trực của đoạn thẳng HK
C. AD là tia phân giác của góc HAK
D. Cả A, B, C đều đúng
Cho tam giác ABC vuông tại A, kẻ đường cao AH . trên cạnh AC lấy điểm K sao cho AK=AH. Kẻ KD vuông góc với AC tại K (D thuộc BC) chứng minh
a) tam giác AHD = tam giác AKD
b) AD là đường trung trực của đoạn thẳng HK
GiẢI:
VẼ DG vuông góc vối AH (G thuộc AH). Suy ra: DG//BC.
Ta có:
Góc BAH = góc BCA ( cùng phụ góc B)
Mà góc BCA = góc GDA (góc trong cùng phía)
Do đó: góc BAH = góc GDA
Xét hai tam giác ABH và DAG, ta có:
ü góc BAH = góc GDA (chứng minh trên)
ü AB=AD ( giả thuyết)
ü ABH vuông tại H, và AHG vuông tại G.
Nếu học tới các trường hợp bằng nhau của tam giác vuông thì ghi là:
Tam giác ABH = tam giác DAG (cạnh huyền góc nhon)
Nếu chưa học tới thì ghi:
Tam giác ABH = tam giác DAG (góc cạnh góc)
Suy ra: AH=DG
Lại có: DG=HE (vì EDGH là hình chủ nhật)
Vậy AH=HE
Cho tam giác ABC vuông tại A (AB<AC), đường cao AH H thuộc BC. Trên cạnh BC lấy điểm D sao cho BD = BA
a/ C/m: Tam giác ABD cân và AD là tia phân giác của góc HAC
b/ Kẻ DK vuông góc với AC (K thuộc AC) C/m AK = AH
Bài 4. (2,5 điểm) Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Trên cạnh ^ C lfy điểm E sao cho AH = AE Từ E kẻ đường thẳng vuông góc với AC, cắt BC tại D. a) Chimg minh Delta*AHD = Delta*AED b) So sinh DH và DC c) Gọi K là giao điểm của DE và AH. Chứng minh AD KC
`a,`
Xét `2 \Delta` vuông `AHD` và ` AED`:
\(\text{AD chung}\)
\(\text{AH = AE (gt)}\)
`=> \Delta AHD = \Delta AED (ch-cgv)`
`b,`
Vì `\Delta AHD = \Delta AED (a)`
`->`\(\text{DH = DE (2 cạnh tương ứng) (1)}\)
\(\text{Xét }\Delta\text{DEC :}\)
\(\widehat{\text{DEC}}=90^0\)
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`->`\(\text{DC là cạnh lớn nhất}\)
`->`\(\text{DC > DE (2)}\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
`->`\(\text{DC > DH.}\)
`c,` cho mình bỏ câu này;-;;; xin lỗi cậu nhiều;-;.
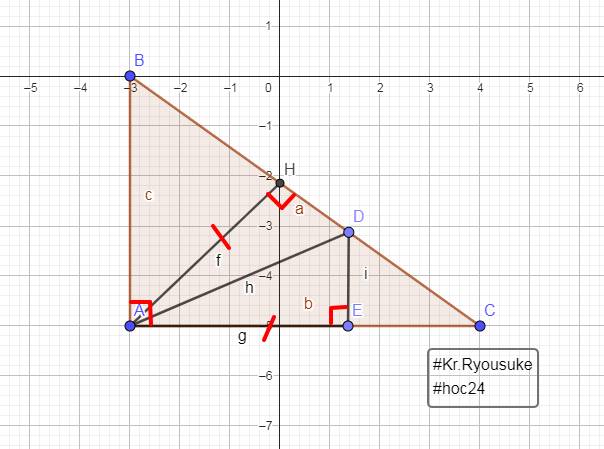
Cho tam giác ABC vuông tại A (AB<AC), đường cao AH H thuộc BC. Trên cạnh BC lấy điểm D sao cho BD = BA
a/ C/m: Tam giác ABD cân và AD là tia phân giác của góc HAC
b/ Kẻ DK vuông góc với AC (K thuộc AC ) Chứng minh AK = AH