Áp dụng tính chất của dãy tỉ số bằng nhau ta có : 

\(\frac{x}{8}=\frac{y}{3}=\frac{2x}{16}=\frac{3y}{9}=\frac{2x+3y}{16+9}=\frac{50}{25}=2\)

Nên : x/8 = 2 => x = 16

         y/3 = 2 => y = 6

Vậy x = 16 ; y = 6 . 

Bài 1: 

a: \(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x+y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)

b: \(\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\4x+2y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\2x=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)

a/ 

<=> 5x = 10

=> x = 2 

thay x vào 3.x - y = 3

=> y = 3

b/ <=> 6x +4y = 10

2 ( 3x + 2y ) = 10

=> 3x + 2y = 5

=> x= 3  . y = -2 

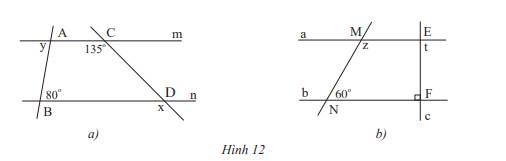
a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)

b)

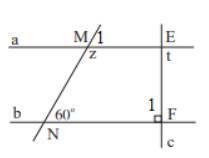
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)

Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)

Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)

120^o

C

C.  120o   

Câu 4:B

Câu 7: A

Câu 8: B

Câu 11: C

Vecto pháp tuyến của đường thẳng \({d_1}\) là: \(\overrightarrow {{n_1}}  = \left( {2; - 1} \right)\)

Vecto pháp tuyến của đường thẳng \({d_2}\) là: \(\overrightarrow {{n_2}}  = \left( {1; - 3} \right)\)

Ta có:  \(\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)

Vậy \(\left( {{d_1},{d_2}} \right) = {45^o}\)