giải giúp mình bài 5 câu 3 với!

 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Giải giúp mình bài 3 câu 4 với
Trong mp đáy, qua B kẻ đường thẳng song song AC, lần lượt cắt DA và DC kéo dài tại E và F
\(\Rightarrow AC||\left(SEF\right)\Rightarrow d\left(AC;SB\right)=d\left(AC;\left(SEF\right)\right)=d\left(A;\left(SEF\right)\right)\)
Gọi I là giao điểm AC và BD
Theo định lý Talet: \(\dfrac{ID}{IB}=\dfrac{DC}{AB}=3\Rightarrow\dfrac{ID}{BD}=\dfrac{3}{4}\)
Cũng theo Talet: \(\dfrac{DA}{DE}=\dfrac{DI}{DB}=\dfrac{3}{4}\Rightarrow AD=\dfrac{3}{4}DE\Rightarrow AE=\dfrac{1}{4}DE\)
\(\Rightarrow d\left(A;\left(SEF\right)\right)=\dfrac{1}{4}d\left(D;\left(SEF\right)\right)\)
Trong tam giác vuông EDF, kẻ \(DH\perp EF\) , trong tam giác vuông SDH, kẻ \(DK\perp SH\)
\(\Rightarrow DK\perp\left(SEF\right)\Rightarrow DK=d\left(D;\left(SEF\right)\right)\)
\(DE=\dfrac{4}{3}AD=\dfrac{4a}{3}\); \(DF=\dfrac{4}{3}DC=4a\)
\(\dfrac{1}{DH^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}=\dfrac{5}{8a^2}\)
\(\dfrac{1}{DK^2}=\dfrac{1}{SD^2}+\dfrac{1}{DH^2}=\dfrac{1}{48a^2}+\dfrac{5}{8a^2}\Rightarrow DK=\dfrac{4a\sqrt{93}}{31}\)
\(\Rightarrow d\left(AC;SB\right)=\dfrac{1}{4}DK=\dfrac{a\sqrt{93}}{31}\)
giải gấp giúp mình câu 3 bài 2 với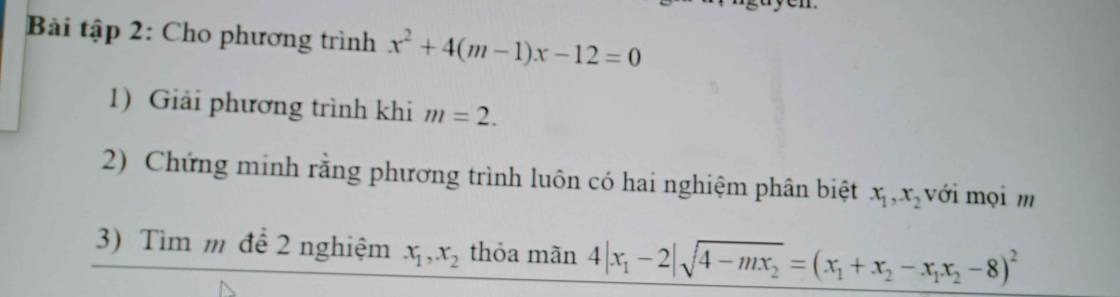
1: Thay m=2 vào phương trình, ta được:
\(x^2+4\left(2-1\right)x-12=0\)
=>\(x^2+4x-12=0\)
=>(x+6)(x-2)=0
=>\(\left[\begin{array}{l}x+6=0\\ x-2=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-6\\ x=2\end{array}\right.\)
2: \(x^2+4\left(m-1\right)x-12=0\)
a=1; b=4(m-1); c=-12
Vì \(a\cdot c=1\cdot\left(-12\right)=-12<0\)
nên phương trình luôn có hai nghiệm phân biệt trái dấu với mọi m
3: Theo Vi-et, ta có:
\(\begin{cases}x_1+x_2=-\frac{b}{a}=-4\left(m-1\right)\\ x_1x_2=\frac{c}{a}=-12\end{cases}\)
Vì x1 là nghiệm của phương trình nên ta có: \(x_1^2+4\left(m-1\right)\cdot x_1-12=0\)
=>\(x_1^2+4m\cdot x_1-4x_1-12=0\)
=>\(x_1^2-4x_1+4+4m\cdot x_1-16=0\)
=>\(\left(x_1-2\right)^2=-4mx_1+16=4\left(-mx_1+4\right)\)
=>\(\left|x_1-2\right|=\sqrt{4\left(-mx_1+4\right)}=2\cdot\sqrt{-mx_1+4}\)
\(4\left|x_1-2\right|\cdot\sqrt{4-mx_2}=\left(x_1+x_2-x_1x_2-8\right)^2\)
=>\(4\cdot2\cdot\sqrt{4-mx_1}\cdot\sqrt{4-mx_2}=\left(-4m+4+12-8\right)^2=\left(-4m+8\right)^2\)
=>\(8\cdot\sqrt{16-4mx_2-4mx_1+m^2\cdot x_1x_2}=16\cdot\left(m-2\right)^2\)
=>\(\sqrt{m^2\cdot\left(-12\right)-4m\left(x_1+x_2\right)+16}=2\cdot\left(m-2\right)^2\)
=>\(\sqrt{-12m^2-4m\cdot\left(-4m+4\right)+16}=2\left(m-2\right)^2\)
=>\(\sqrt{-12m^2+16m^2-16m+16}=2\left(m-2\right)^2\)
=>\(\sqrt{4m^2-16m+16}=2\left(m-2\right)^2\)
=>\(2\cdot\sqrt{m^2-4m+4}=2\left(m-2\right)^2\)
=>\(\left|m-2\right|=\left(m-2\right)^2\)
=>m-2=0
=>m=2
Giải giúp mình bài 3 câu c với ạ
c: (x-2)^2+2(2-x)=0
=>(x-2)^2-2(x-2)=0
=>(x-2)(x-4)=0
=>x=2 hoặc x=4
Làm giúp mình với , bài 5 đó nha câu 1,2,3,4,5,6,7,8,9,10 và giải thích nữa nha


làm giúp mình câu 5 :câu 3 với!giải dõ hộ mình với ạ!
Câu 1: D
Câu 2: C
Câu 3: C
Câu 4: D
Câu 5: A
Giải giúp mình bài này với ạ giải câu c chi tiết xíu giúp mình với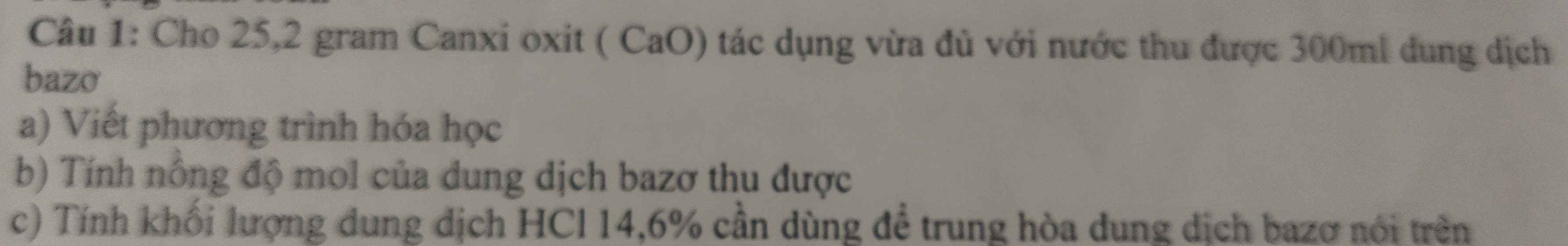
giải giúp mình bài 4 câu 3 với cần gấp lắm ạ
a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được
giúp mình bài 4 và 5 với ạ câu đã có lời giải thì ko cần làm ạ