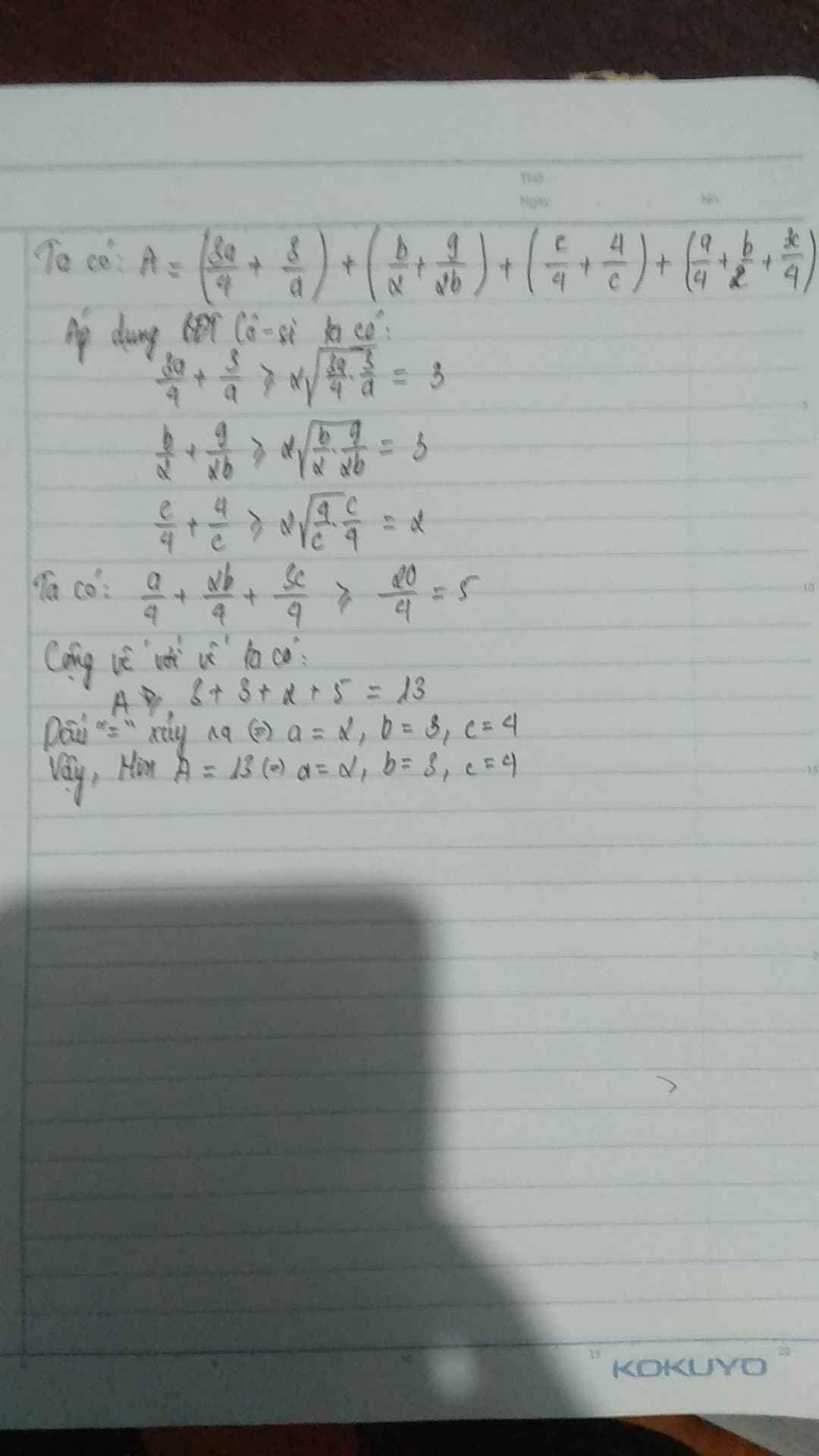vỗ tay :) bài kt của thầy Hiệp ak

Ta có

\(M+3=\left(\frac{2b+3c+16}{1+6a}+1\right)+\left(\frac{6a+3c+16}{1+2b}+1\right)+\left(\frac{6a+2b+16}{1+3c}+1\right)\)

=> \(M+3=\left(6a+2b+3c+17\right)\left(\frac{1}{1+6a}+\frac{1}{1+2b}+\frac{1}{1+3c}\right)\)

=> \(M+3=28\left(\frac{1}{1+6a}+\frac{1}{1+2b}+\frac{1}{1+3c}\right)\ge28.\frac{9}{3+6a+2b+3c}=28.\frac{9}{14}=18\)

=> \(M\ge15\)

vậy MinM=15 khi \(a=\frac{11}{18};b=\frac{11}{6};c=\frac{11}{9}\)

Lời giải:

Biến đổi $A$ :

\(A=a+b+c+\frac{3}{a}+\frac{9}{2b}+\frac{4}{c}=\frac{1}{4}(a+2b+3c)+\left(\frac{3a}{4}+\frac{3}{a}\right)+\left (\frac{b}{2}+\frac{9}{2b}\right)+\left (\frac{c}{4}+\frac{4}{c}\right)\)

Ta có: \(\frac{1}{4}(a+2b+3c)\geq \frac{20}{4}=5\)

Áp dụng BĐT AM-GM: \(\left\{\begin{matrix} \frac{3a}{4}+\frac{3}{a}\geq 3\\ \frac{b}{2}+\frac{9}{2b}\geq 3\\ \frac{c}{4}+\frac{4}{c}\geq 2\end{matrix}\right.\)

Do đó \(A\geq 5+3+3+2=13\) hay \(A_{\min}=13\)

Dấu bằng xảy ra khi \(\left\{\begin{matrix} a=2\\ b=3\\ c=4\end{matrix}\right.\)

Mấu chốt của bài toán là cách tìm điểm rơi.

đặt 

\(A=a+b+c+\dfrac{3}{a}+\dfrac{9}{2b}+\dfrac{4}{c}\)

\(=>4A=4a+4b+4c+\dfrac{12}{a}+\dfrac{36}{2b}+\dfrac{16}{c}\)

\(=>4A=a+2b+3c+3a+\dfrac{12}{a}+2b+\dfrac{36}{2b}+c+\dfrac{16}{c}\)

áp dụng BDT AM-GM

\(=>\dfrac{12}{a}+3a\ge2\sqrt{12.3}=12\)

\(=>2b+\dfrac{36}{2b}\ge2\sqrt{36}=12\)

\(=>c+\dfrac{16}{c}\ge2\sqrt{16}=8\)

\(=>4A\ge20+12+12+8=52=>A\ge13\)

dấu"=" xảy ra<=>a=2,b=3,c=4

\(S=a+b+c+\frac{3}{a}+\frac{9}{2b}+\frac{4}{c}\)

\(=\left(\frac{3a}{4}+\frac{3}{a}\right)+\left(\frac{b}{2}+\frac{9}{2b}\right)+\left(\frac{c}{4}+\frac{4}{c}\right)+\frac{1}{4}\left(a+2b+3c\right)\)

\(\ge2\sqrt{\frac{3a}{4}.\frac{3}{a}}+2\sqrt{\frac{b}{2}.\frac{9}{2b}}+2\sqrt{\frac{c}{4}.\frac{4}{c}}+\frac{1}{4}.20\)

\(\Rightarrow S\ge13\)

Đẳng thức xảy ra khi a = 2, b = 3, c = 4

Vậy minS = 13 tại (a,b,c) = (2,3,4)

Ai giúp đi.

Ngọc