Cho parabol (P) : y = -x2 và đường thẳng (d) có hệ số góc m đi qua điểm M(-1 ; -2) .
a). Chứng minh rằng với mọi giá trị của m (d) luôn cắt (P) tại hai điểm A , B phân biệt
b). Xác định m để A,B nằm về hai phía của trục tung

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho Parabol(P): y=x2 và đường thẳng (d): y=2(m+1)x-m2-4 (1), (m là tham số)
a) Tìm m để đường thẳng (d) đi qua A(0;-5)
b) Với giá trị nào của m để đường thẳng (d) cắt parabol (P) tại 2 điểm phân biệt có hoành độ x1; x2 thỏa mãn điều kiện: (2x1-1)(x22-2mx2+m2+3)=21
a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d):\(y=2x-m+1\) (với m là tham số) và parabol (P): .
a) Tìm m để đường thẳng (d) đi qua điểm A (–1; 3).
b) Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có tọa độ (x1; y1) và (x2; y2) sao cho \(x_1x_2\left(y_1+y_2\right)+6=0\) .
a: Thay x=-1 và y=3 vào (d), ta được:
-2-m+1=3
=>-1-m=3
=>m+1=-3
hay m=-4
Đúng 1
Bình luận (1)
Bài 1: Cho parabol (P) : y = x2 và đường thẳng (d) : y= 3mx + 1 - m2 ( m là tham số)
a) TÌm m để (d) đường thẳng đi qua A( 1; -9)
b) Tìm m để (d) m cắt (P) tại 2 điểm phân biệt có hoành độ x1; x2 thõa mãn x1 + x2 = 2x1x2
Bài 1:
a) Để (d) đi qua A(1;-9) thì
Thay x=1 và y=-9 vào (d), ta được:
\(3m\cdot1+1-m^2=-9\)
\(\Leftrightarrow-m^2+3m+1+9=0\)
\(\Leftrightarrow m^2-3m-10=0\)
\(\Leftrightarrow m^2-5m+2m-10=0\)
\(\Leftrightarrow m\left(m-5\right)+2\left(m-5\right)=0\)
\(\Leftrightarrow\left(m-5\right)\left(m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-5=0\\m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=5\\m=-2\end{matrix}\right.\)
Vậy: Để (d) đi qua A(1;-9) thì \(m\in\left\{5;-2\right\}\)
Đúng 0
Bình luận (0)
cho parabol (P) : y= -x2 -1 và đường thẳng (d) đi qua điểm I (0;-2) và có hệ số góc k
a) tìm k để (d) cắt (P) tại 2 điểm phân biệt
b) gọi A,B là các giao điểm của (d) và (p) và có hoành độ lầ lượt là x1,x2 , tìm k để trung điểm của đoạn thẳng AB nằm trên trục tung
2/ Cho parabol (P): y=x2
và đường thẳng (d) có hệ số góc là a khác 0 đi qua điểm M(1;2)
a/ Cm rằng (d) luôn luôn cắt P tại hai điểm phân biệt với mọi a khác 0.
b/ Gọi xA và xB là hoành độ giao điểm của P và d. Chứng minh rằng xA+xB-xA.xB=2.
Bài này sử dựng định lý viet để chứng minh:
Gọi phương trình đường thẳng (d) có hệ số góc a có dạng : \(y=ax+b\left(a\ne0\right)\); \(M\left(1,2\right)\)thuộc (d) nên : \(2=a+b\Rightarrow b=2-a\left(1\right)\). Xét phương trình hoành độ giao điểm có : \(x^2=ax+b\left(2\right)\)thế 1 vào 2 có \(x^2=ax+2-a\Leftrightarrow x^2-ax-\left(2-a\right)=0\)phương trình có : \(\Delta=a^2+4\left(2-a\right)=a^2-4a+8\)\(\Rightarrow\Delta=\left(a^2-4a+4\right)+4=\left(a-2\right)^2+4\ge4\forall a\) nên phương trình luôn có hai nghiệm phân biệt với mọi giá tri của \(a\ne0\)Khi đó parabol cắt d tại hai điểm A,B với A,B có hoành độ lần lượt là \(x_A,x_B\) theo vi ét ta có : \(\hept{\begin{cases}x_A+x_B=a\\x_Ax_B=-\left(2-a\right)\end{cases}}\)ta xét \(x_A+x_B-x_Ax_B=a+\left(2-a\right)=2\left(dpcm\right)\)
Đúng 0
Bình luận (0)
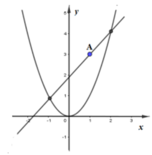
Cho parabol (P) có phương trình
y
x
2
và đường thẳng d đi qua A(1;3). Giả sử khi đường thẳng d có hệ số góc k thì diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d là nhỏ nhất. Giá trị thực của k thuộc khoảng nào sau đây? A.
3
;
+
∞
B.
−
∞
;...
Đọc tiếp
Cho parabol (P) có phương trình y = x 2 và đường thẳng d đi qua A(1;3). Giả sử khi đường thẳng d có hệ số góc k thì diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d là nhỏ nhất. Giá trị thực của k thuộc khoảng nào sau đây?
A. 3 ; + ∞
B. − ∞ ; − 3
C. (0;3)
D. (-3;0)
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số
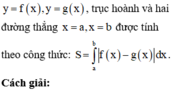

Diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d:
S = ∫ x 1 x 2 k x − k + 3 − x 2 d x = 1 2 k x 2 − k − 3 x − 1 3 x 3 x 2 x 1 = 1 2 k x 1 2 − k − 3 x 1 − 1 3 x 1 3 − 1 2 k x 2 2 − k − 3 x 2 − 1 3 x 2 3 = 1 2 k x 1 2 − x 2 2 − k − 3 x 1 − x 2 − 1 3 x 1 3 − x 2 3 = x 1 − x 2 1 2 k x 1 + x 2 − k − 3 − 1 3 x 1 + x 2 2 − x 1 x 2 = x 1 − x 2 1 2 k . k − k − 3 − 1 3 k 2 − k − 3 = x 1 − x 2 1 6 k 2 − 2 3 k + 2
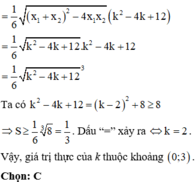
Đúng 0
Bình luận (0)
Cho hàm số y = x2 có đồ thị là Parabol (P)
a) Vẽ đồ thị hàm số đã cho trên mặt phẳng tọa độ Oxy
b) Viết phương trình đường thẳng (d) đi qua điểm nằm trên Parabol (P) có hoành độ x = 2 và có hệ số góc k. Với giá trị k nào thì (d) tiếp xúc (P) ?
Cho parabol (p) y=2x^2 và đường thẳng (d) y=3mx+1-m^2 (m là tham số) a. Tìm m để (d) đi qua A (-1; 9) b. Tìm m để (d) cắt (p) tại hai điểm phân biệt có hoành độ x1, x2 thoả mãn x1+x2 = 2x1×x2
a) \(A\in\left(d\right)\Rightarrow9=-3m+1-m^2\)
\(\Leftrightarrow m^2+3m+8=0\) \(\Leftrightarrow\left(m+\dfrac{3}{2}\right)^2+\dfrac{23}{4}=0\)(vn)
Vậy không tồn tại m để (d) đi qua A(-1;9)
b) Xét pt hoành độ gđ của (P) và (d) có:
\(2x^2=3mx+1-m^2\)
\(\Leftrightarrow2x^2-3mx-1+m^2=0\)
\(\Delta=9m^2-4.2\left(-1+m^2\right)=m^2+8>0\) với mọi m
=> Pt luôn có hai nghiệm pb => (d) luôn cắt (P) tại hai điểm pb
Theo viet:\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3m}{2}\\x_1x_2=\dfrac{m^2-1}{2}\end{matrix}\right.\)
\(x_1+x_2=2x_1x_2\)
\(\Leftrightarrow\dfrac{3m}{2}=2.\dfrac{m^2-1}{2}\) \(\Leftrightarrow2m^2-3m-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-\dfrac{1}{2}\end{matrix}\right.\)
Vậy...
Đúng 3
Bình luận (0)
Trong mặt phẳng Oxy, cho parabol P : y = -x 2 và đường thẳng d đi qua điểm M 0;-1 có hệ số góc k. c Viết phương trình đường thẳng d . Chứng minh rằng với mọi giá trị của ,k d luôn cắt P tại hai điểm phân biệt A,B. giúp mình nha

















