giúp toi câu a với:>
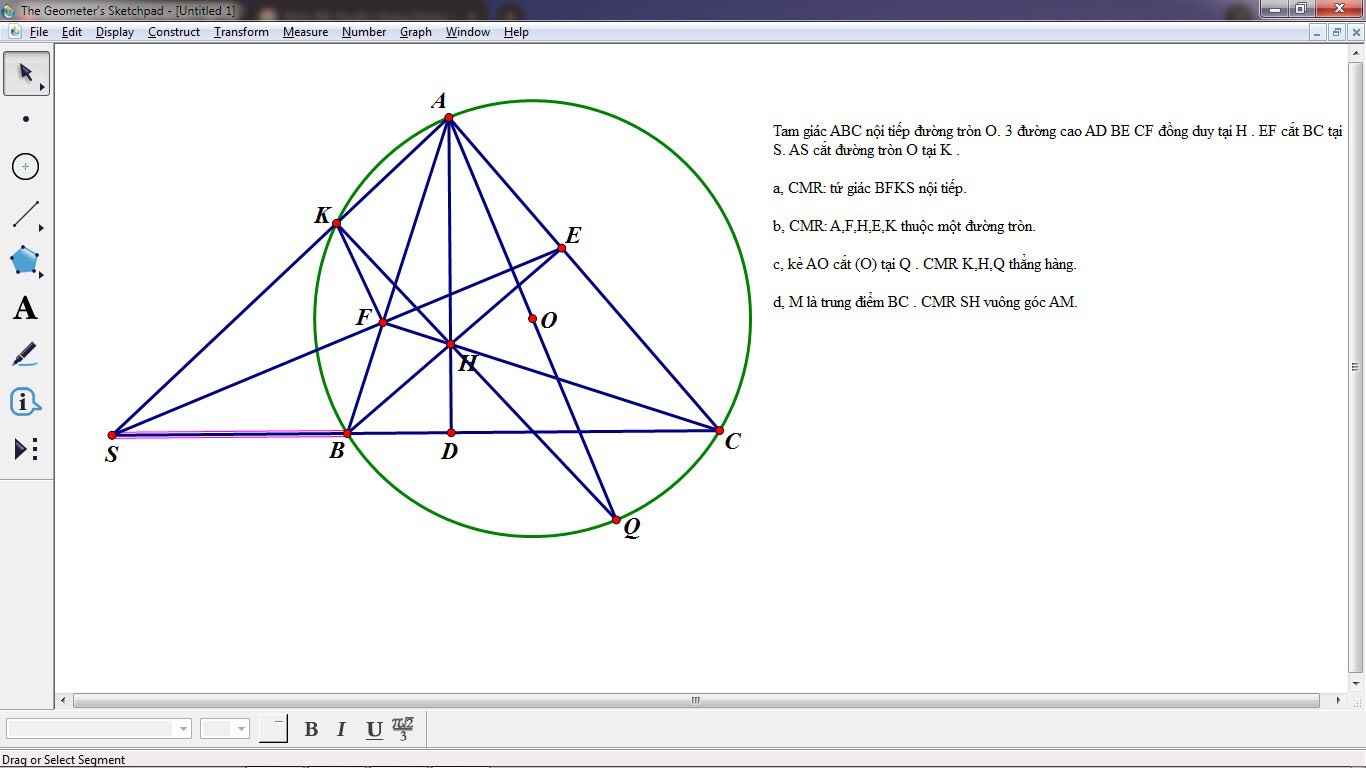
vẽ hình làm câu a giúp toi với:))tks ah

giúp toi 2 câu này với:>
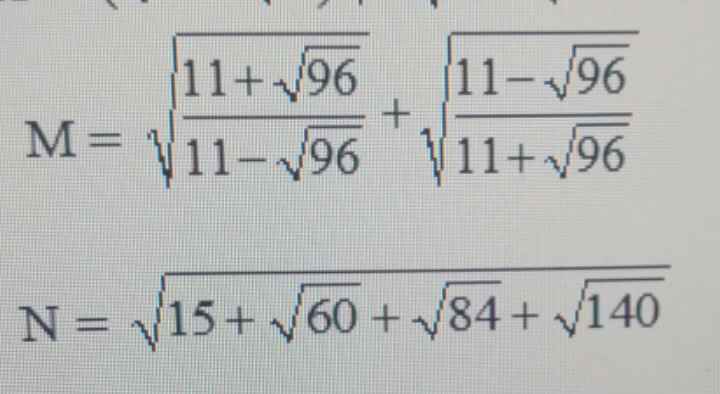
\(M=\sqrt{\dfrac{11+\sqrt{96}}{11-\sqrt{96}}}+\sqrt{\dfrac{11-\sqrt{96}}{11+\sqrt{96}}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{121-96}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{121-96}}\)
\(\Rightarrow M=\sqrt{\dfrac{\left(11+\sqrt{96}\right)^2}{25}}+\sqrt{\dfrac{\left(11-\sqrt{96}\right)^2}{25}}\)
\(\Rightarrow M=\dfrac{11+\sqrt{96}}{5}+\dfrac{11-\sqrt{96}}{5}\)
\(\Rightarrow M=\dfrac{22}{5}\)
\(N=\sqrt{15+2\sqrt{15}+2\sqrt{21}+2\sqrt{35}}\\ N=\sqrt{3+5+7+2\sqrt{3}\sqrt{5}+2\sqrt{3}\sqrt{7}+2\sqrt{5}\sqrt{7}}\\ N=\sqrt{\left(\sqrt{3}+\sqrt{5}+\sqrt{7}\right)^2}=\sqrt{3}+\sqrt{5}+\sqrt{7}\)
giúp toi câu c với:))tks

giải đầy đủ giúp toi câu 2c với:))tks ah

a: Thay x=16 vào B, ta được:
\(B=\dfrac{4+3}{4-2}=\dfrac{7}{2}\)
giúp toi câu này:>tks
ĐK của A:\(\chi\ge0;\chi\ne1\)

\(P=A\left(3-x+2\sqrt{x}\right)=A\left(3-\sqrt{x}\right)\left(\sqrt{x}+1\right)\\ P=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\left(3-\sqrt{x}\right)\left(\sqrt{x}+1\right)=\left(2\sqrt{x}-1\right)\left(3-\sqrt{x}\right)\\ P=6\sqrt{x}-2x-3+\sqrt{x}=-2x+7\sqrt{x}-3\\ P=-2\left(x-2\cdot\dfrac{7}{4}\sqrt{x}+\dfrac{49}{16}-\dfrac{49}{16}\right)-3\\ P=-2\left(\sqrt{x}-\dfrac{7}{4}\right)^2+\dfrac{49}{8}-3\le\dfrac{49}{8}-3=\dfrac{25}{8}\\ P_{max}=\dfrac{25}{8}\Leftrightarrow\sqrt{x}=\dfrac{7}{4}\Leftrightarrow x=\dfrac{49}{16}\)
Giúp toi câu 6 ae ơi
Giúp toi duy nhất câu C thui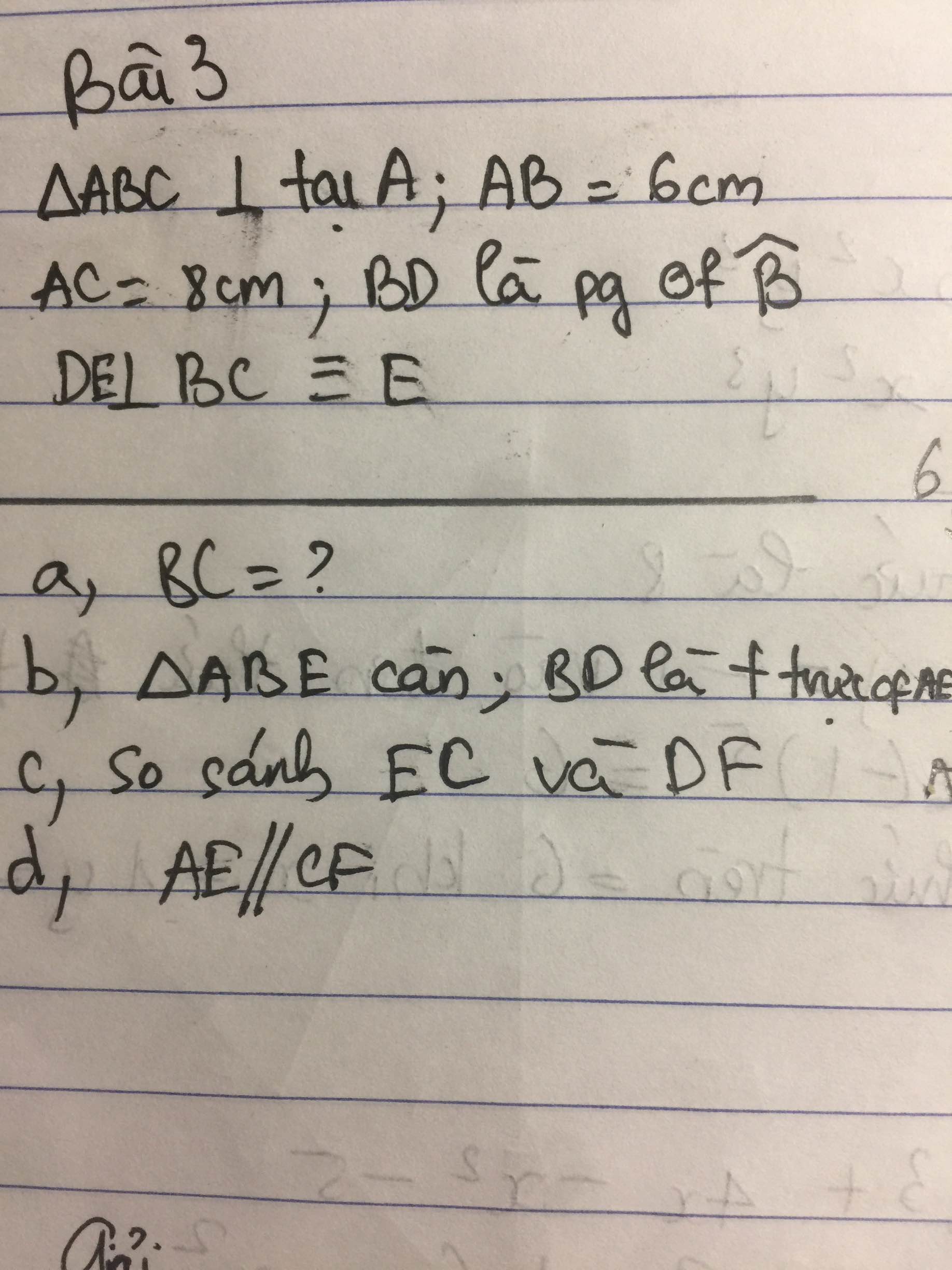
c) Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: AF=EC(Hai cạnh tương ứng)
mà AF<DF(ΔADF vuông tại A)
nên EC<DF(đpcm)
d) Xét ΔBFC có
\(\dfrac{BA}{AF}=\dfrac{BE}{EC}\left(BA=BE;AF=EC\right)\)
nên AE//FC(Định lí Ta lét đảo)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
b) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)
Suy ra: BA=BE(Hai cạnh tương ứng) và DA=DE(Hai cạnh tương ứng)
Xét ΔABE có BA=BE(cmt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Ta có: BA=BE(cmt)
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
Cho phan so a/b la phan so toi gian. Hoi a/a+b co phai la phan so toi gian ko
giúp mình với!!!!
Cho phan so a/b la phan so toi gian. Hoi a/a+b co phai la phan so toi gian ko
Answer : Ex : \(\frac{1}{2}\)là phân số tối giản còn \(\frac{\frac{1}{1}}{2}=2\)là số tự nhiên chứ ko phải là phân số
toi cần bài giải chi tiết, ai bt giúp toi với
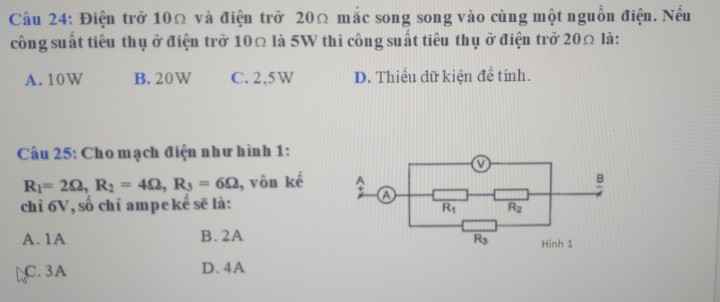
25.
\(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(2+4\right)6}{2+4+6}=3\Omega\)
\(\Rightarrow I=\dfrac{U}{R}=\dfrac{6}{3}=2A\)
Chọn B
Câu 24.
Hai điện trở cùng mắc song song vào một mạch\(\Rightarrow U_1=U_2=U_m\) \(\Rightarrow P_1\cdot R_1=P_2\cdot R_2\)
\(\Rightarrow P_2=\dfrac{P_1\cdot R_1}{R_2}=\dfrac{5\cdot10}{20}=2,5W\)
Chọn C.
Câu 25.
\(\left(R_1ntR_2\right)//R_3\)
\(R_{tđ}=\dfrac{\left(R_1+R_2\right)\cdot R_3}{R_1+R_2+R_3}=\dfrac{\left(2+4\right)\cdot6}{2+4+6}=3\Omega\)
\(I_A=I_m=\dfrac{U_V}{R_{tđ}}=\dfrac{6}{3}=2A\)
Chọn B.