29.

\(y'=\dfrac{1}{3}x^3-\dfrac{1}{2}\left(m^2+1\right)x^2+\left(m^2-7m+12\right)x\)

\(y''=x^2-\left(m^2+1\right)x+m^2-7m+12\)

Pt \(y''=0\) có 2 nghiệm trái dấu khi và chỉ khi:

\(1.\left(m^2-7m+12\right)< 0\)

\(\Leftrightarrow3< m< 4\)

\(\Rightarrow\) Không có giá trị nguyên nào của m thỏa mãn

30.

\(y'=x^2-2\left(2m+1\right)x-m\ge0;\forall x\)

\(\Leftrightarrow\Delta'=\left(2m+1\right)^2+m\le0\)

\(\Leftrightarrow4m^2+5m+1\le0\)

\(\Leftrightarrow-1\le m\le-\dfrac{1}{4}\)

\(\Rightarrow\) Có 1 giá trị nguyên của m thỏa mãn (\(m=-1\))

Câu 12.

Ta có: \(\dfrac{sini}{sinr}=n\Rightarrow\dfrac{sin60^o}{sinr}=1,5\)

\(\Rightarrow sinr=\dfrac{\sqrt{3}}{3}\)

\(\Rightarrow r\approx35,3^o\)

Chọn C

\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}\dfrac{\sqrt{x^2+7}-4}{2x-6}=\lim\limits_{x\rightarrow3}\dfrac{x^2-9}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}\)

\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}=\lim\limits_{x\rightarrow3}\dfrac{x+3}{2\left(\sqrt{x^2+7}+4\right)}\)

\(=\dfrac{6}{2\left(4+4\right)}=\dfrac{3}{8}\)

\(f\left(3\right)=1-2m\)

Hàm liên tục trên R khi: 

\(1-2m=\dfrac{3}{8}\Rightarrow m=\dfrac{5}{16}\in\left(0;1\right)\)

38.

\(y'=2x^2-8x+9=2\left(x-2\right)^2+1\ge1\)

\(\Rightarrow\) Tiếp tuyến có hệ số góc nhỏ nhất bằng 1 khi \(x_0-2=0\Rightarrow x_0=2\)

\(y\left(2\right)=-\dfrac{11}{3}\)

Phương trình d:

\(y=1\left(x-2\right)-\dfrac{11}{3}=x-\dfrac{17}{3}\)

Thay tọa độ 4 điểm của đáp án, chỉ có \(P\left(5;-\dfrac{2}{3}\right)\) thỏa mãn

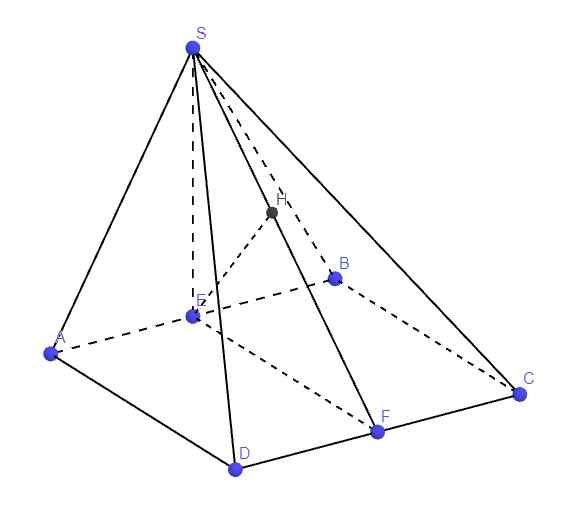
39.

Gọi E là trung điểm AB, F là trung điểm CD

Từ E kẻ EH vuông góc SF (H thuộc SF)

Do tam giác SAB đều \(\Rightarrow SE\perp AB\Rightarrow SE\perp\left(ABCD\right)\)

\(\Rightarrow SE\perp CD\)

\(EF||AD\Rightarrow EF\perp CD\)

\(\Rightarrow CD\perp\left(SEF\right)\) \(\Rightarrow CD\perp EH\)

\(\Rightarrow EH\perp\left(SCD\right)\Rightarrow EH=d\left(E;\left(SCD\right)\right)\)

Lai có: \(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(E;\left(SCD\right)\right)=EH\)

\(SE=\dfrac{AB\sqrt{3}}{2}=\dfrac{\sqrt{3}}{2}\) ; \(EF=AD=1\)

Hệ thức lượng: \(d=HE=\dfrac{SE.EF}{\sqrt{SE^2+EF^2}}=\dfrac{\sqrt{21}}{7}\)

Hình vẽ câu 39:

Hi bạn, câu 29 này mình có cái cách này dùng cho các bài lim khi rơi vào trường hợp vô định thì bạn dùng quy tắc L'Hospital làm cho nhanh với trường hợp các bài trắc nghiệm như thế này

Ở bài 29 này đang rơi vào dạng \(\dfrac{0}{0}\) nên dùng quy tắc L'Hospital được nè. Bạn làm như sau:

ĐKXĐ: \(\left\{{}\begin{matrix}x\ne1\\x\ge-3\end{matrix}\right.\)

Bước 1: Đạo hàm tử mẫu, ta được: \(\dfrac{\dfrac{1}{2}\left(x+3\right)^{-\dfrac{1}{2}}}{1}\)

Bước 2: Thay điểm cần tính giới hạn: (x=1)

ta sẽ được \(\dfrac{1}{4}\)

Vậy \(lim_{x\rightarrow1}\dfrac{\sqrt{x+3}-2}{x-1}=\dfrac{1}{4}\)

\(\Rightarrow a=1;b=4\)

Vậy S=4a-b=0

a: BA vuông góc AD

BA vuông góc SA

=>BA vuông góc (SAD)

b: CD vuông góc AD

CD vuông góc SA

=>CD vuông góc (SAD)

=>(SCD) vuông góc (SAD)

c: (SD;(ABCD))=(DS;DA)=góc SDA

tan SDA=SA/AD=căn 6/2

=>góc SDA=51 độ

\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{mx^2-\left(m+3\right)x+3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(mx-3\right)}{x-1}\)

\(=\lim\limits_{x\rightarrow1}\left(mx-3\right)=m-3\)

\(f\left(1\right)=m^2-15\)

Hàm liên tục tại \(x=1\) khi:

\(m-3=m^2-15\Rightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)

\(4^2+\left(-3\right)^2=25\)

\(y'=3x^2-2\)

hệ số góc tiếp tuyến tại điểm có hoành độ \(x_0=-1\) là \(y'\left(-1\right)\)

\(y'\left(-1\right)=3.\left(-1\right)^2-2=1\)

19. Giới hạn đã cho hữu hạn khi và chỉ khi \(a=1\)

Khi đó:

\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx-2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-\left(x^2+bx-2\right)}{x+\sqrt{x^2+bx-2}}\)

\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx+2}{x+\sqrt{x^2+bx-2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-b+\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}-\dfrac{2}{x^2}}}=-\dfrac{b}{2}\)

\(\Rightarrow-\dfrac{b}{2}=3\Rightarrow b=-6\Rightarrow a+b=1+\left(-6\right)=-5\)

20.

\(\lim\limits_{x\rightarrow+\infty}\left(x^3+2x-1\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{2}{x^2}-\dfrac{1}{x^3}\right)=+\infty.1=+\infty\)