
giúp mik bài này với mik đang cần gấp
Mik đang cần gấp bài này mọi người giúp mik với ạ. Tối nay mik phải nộp rồi.

uses crt;
var st:string;
d,i,t,x,y,a,b:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do write(st[i]:4);
writeln;
t:=0;
for i:=1 to d do
begin
val(st[i],x,y);
t:=t+x;
end;
writeln(t);
val(st[d],a,b);
if (a mod 2=0) then write(1)
else write(-1);
readln;
end.
Mik đang cần gấp bài này mọi người giúp mik với ạ. Tối nay mik phải nộp rồi.

#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n,t,dem,t1;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
t=0;
for (i=1; i<=n; i++) if (a[i]%2==0) t+=a[i];
cout<<t<<endl;
t1=0;
dem1=0;
for (i=1; i<=n; i++)
if (a[i]<0)
{
cout<<a[i]<<" ";
t1+=a[i];
dem1++;
}
cout<<endl;
cout<<fixed<<setprecision(1)<<(t1*1.0)/(dem1*1.0);
return 0;
}
Mik đang cần gấp bài này mọi người giúp mik với ạ. Tối nay mik phải nộp rồi.

#include <bits/stdc++.h>
using namespace std;
long long a,b;
//chuongtrinhcon
long long gcd(long long a,long long b)
{
if (b==0) return(a);
return gcd(b,a%b);
}
//chuongtrinhchinh
int main()
{
cin>>a>>b;
cout<<max(a,b)<<endl;
cout<<gcd(a,b)<<endl;
if ((a>0 && b>0) or (a<0 && b<0)) cout<<a/gcd(a,b)<<" "<<b/gcd(a,b);
else cout<<"-"<<-a/gcd(-a,b)<<" "<<b/gcd(-a,b);
return 0;
}
mik đang cần bài này gấp các bạn giải hết bài giúp mik nhé mik cần gấp để nộp bài cho thầy
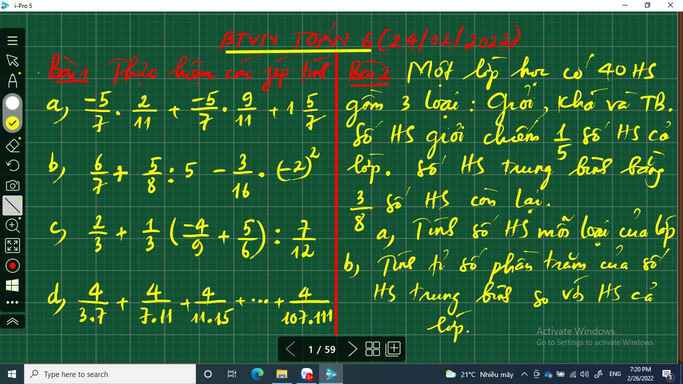
e tách câu hỏi ra nhe tạm thời cj giúp mụt câu nhe
a: \(=\dfrac{-5}{7}\left(\dfrac{2}{11}+\dfrac{9}{11}\right)+1+\dfrac{5}{7}=\dfrac{-5}{7}+1+\dfrac{5}{7}=1\)
b: \(=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{16}\cdot4=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{4}=\dfrac{13}{56}\)
c: \(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{-24+45}{54}\cdot\dfrac{12}{7}\)
\(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{21}{54}\cdot\dfrac{12}{7}=\dfrac{2}{3}+\dfrac{2}{9}=\dfrac{6+2}{9}=\dfrac{8}{9}\)
d: \(=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+...+\dfrac{1}{107}-\dfrac{1}{111}\)
\(=\dfrac{1}{3}-\dfrac{1}{111}=\dfrac{108}{333}=\dfrac{12}{37}\)
Giúp mik bài này vs ạ mik đang cần gấp
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
Giúp mik giả bài này vs, mik đang cần gấp. Giải chi tiếc giùm mik nha.



các bn giúp mik 2 bài này vs ạ! mik đang cần gấp!!!
Ai giúp mik bài này với, mik đang cần gấp lắm!!
mng giúp mik bài này được ko? mik đang cần gấp . cảm ơn bạn nhiều 
a: =>x>=0 và x^2+x=x^2
=>x=0
a: =>x>=1 và 1-x^2=x^2-2x+1
=>-2x^2+2x=0 và x>=1
=>x=1
a: =>x>=1 và 1-2x^2=x^2-2x+1
=>-3x^2+2x=0 và x>=1
=>\(x\in\varnothing\)
a: ĐKXĐ: x<=2 và x^2-2x=x^2-4x+4
=>x=2
a: =>căn x^2-4=x-2
=>x>=2 và x^2-4=x^2-4x+4
=>x>=2 và 4x=8
=>x=2
b: =>x>=0 và x^2-4x+1=x^2
=>-4x+1=0 và x>=0
=>x=1/4
b: =>x>=-1 và x^2+x+1=x^2+2x+1
=>x=0
c: =>x>=1 và 4x^2-8x+1=x^2-2x+1
=>x>=1 và 3x^2-6x=0
=>x=2
b: =>x>=-1 và 5x^2-2x+2=x^2+2x+1
=>x>=-1 và 4x^2-4x+1=0
=>x=1/2
b: =>căn 4x^2-x+1=2x+3
=>x>=-3/2 và 4x^2-x+1=(2x+3)^2=4x^2+12x+9
=>x>=-3/2 và -13x=8
=>x=-8/13
1) \(\sqrt{x^2+x}=x\) (Thỏa mẵn với mọi x)
\(\Leftrightarrow x^2+x=x^2\)
\(\Leftrightarrow x^2+x-x^2=0\)
\(\Leftrightarrow x=0\)
Vậy \(x=0\)
2) \(\sqrt{1-x^2}=x-1\) (ĐK: \(x\le1\) )
\(\Leftrightarrow1-x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-x^2=x^2-2x+1\)
\(\Leftrightarrow-x^2-x^2+2x=1-1\)
\(\Leftrightarrow-2x^2+2x=0\)
\(\Leftrightarrow-2x\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;1\right\}\)
\(\sqrt{1-2x^2}=x-1\) (ĐK: \(x\le\sqrt{\dfrac{1}{2}}\))
\(\Leftrightarrow1-2x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-2x^2=x^2-2x+1\)
\(\Leftrightarrow-2x^2-x^2+2x=1-1\)
\(\Leftrightarrow-3x^2+2x=0\)
\(\Leftrightarrow-x\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=0\\3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=\dfrac{2}{3}\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{2}{3}\right\}\)
\(\sqrt{x^2-2x}=2-x\) (ĐK: \(\left\{{}\begin{matrix}x\le0\\x\ge2\end{matrix}\right.\) )
\(\Leftrightarrow x^2-2x=\left(2-x\right)^2\)
\(\Leftrightarrow x^2-2x=4-4x+x^2\)
\(\Leftrightarrow x^2-x^2-2x+4x=4\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)
\(\sqrt{x^2-4}-x+2=0\) (ĐK: \(\left\{{}\begin{matrix}x\le-2\\x\ge2\end{matrix}\right.\))
\(\Leftrightarrow\sqrt{x^2-4}=x-2\)
\(\Leftrightarrow x^2-4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-4=x^2-4x+4\)
\(\Leftrightarrow x^2-x^2+4x=4+4\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)