MN giúp e gấp vs ạ chi tiết ra giúp e ạ tks 

Những câu hỏi liên quan
Gấp vs ạ mn giải chi tiết giúp e ạ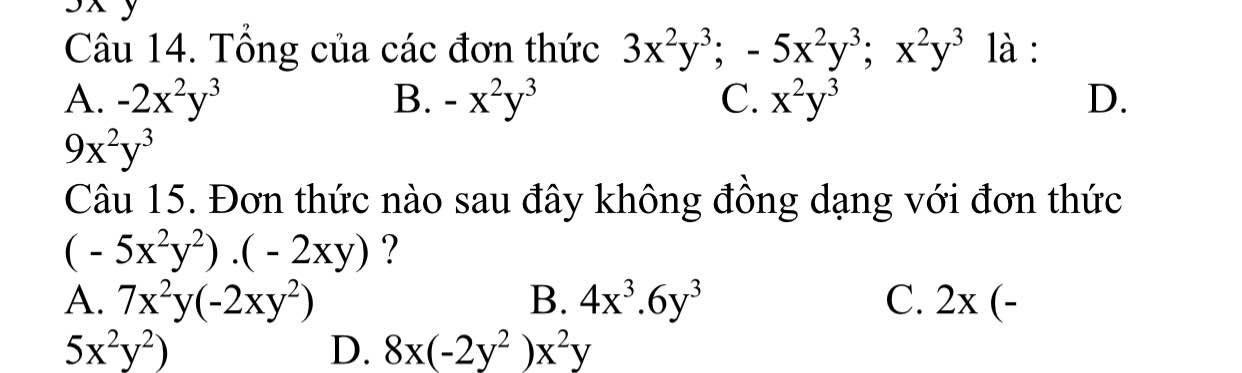
Câu 14: B
Câu 15: Không có câu nào đúng
Đúng 0
Bình luận (0)
Giúp e gấp ạ. Phiền mn chi tiết từng câu giúp e ạ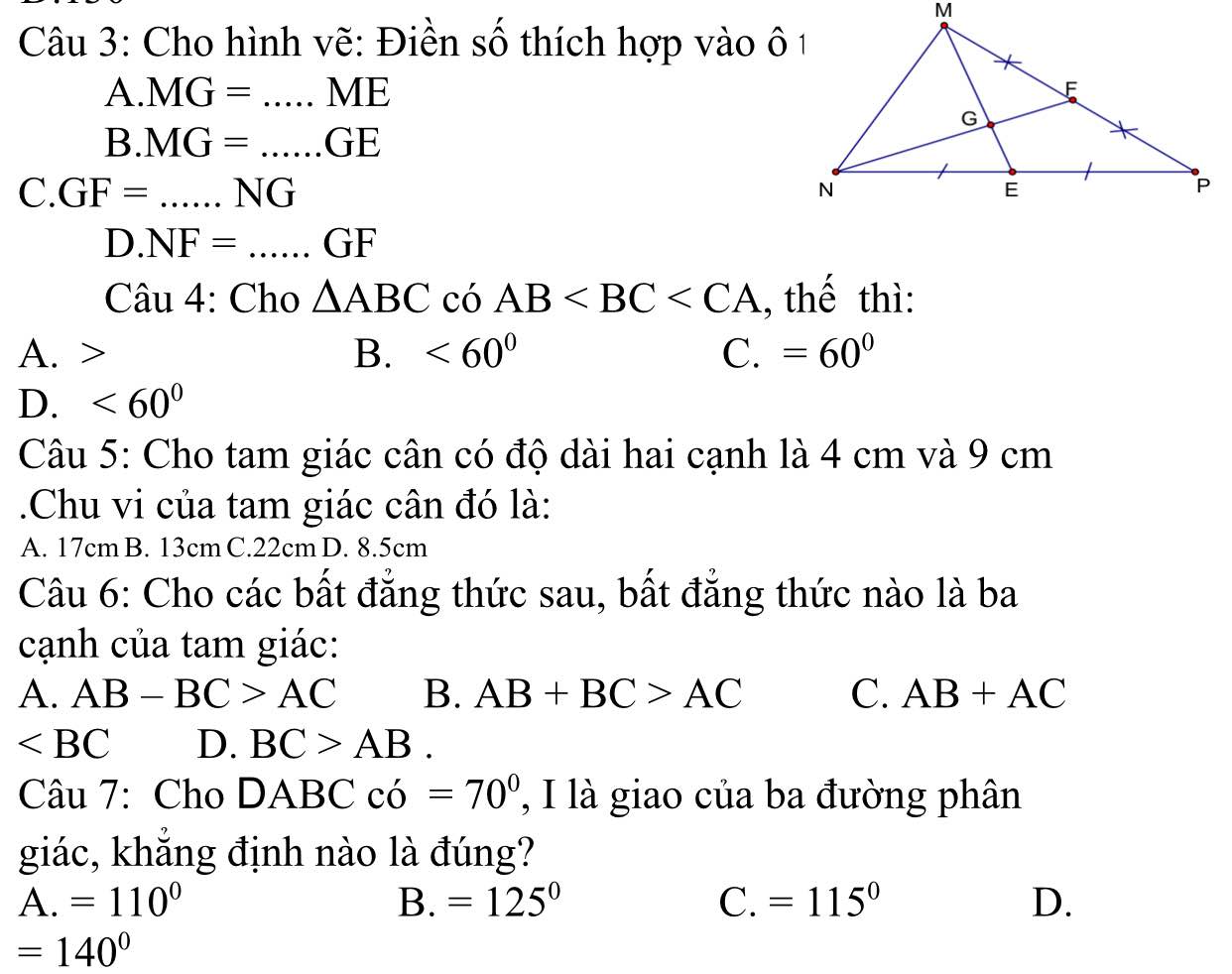
Câu 3:
a) \(MG=\dfrac{2}{3}ME\)
b) MG=2GE
Câu 5: C
Câu 6: B
Đúng 0
Bình luận (0)
Giúp e vs ạ, e cần gấp để hok ạ. Nhanh và chi tiết em sẽ tặng 5*+hay nhất ạ. E xin cảm ơn nhiều! Giúp em trước 3h45p ạ!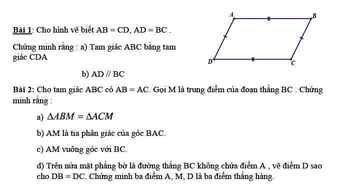
Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Đúng 2
Bình luận (3)
Bài 2:
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó:ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Đúng 1
Bình luận (0)
Mn giúp e vs ak. Tks Mn ạ 
a) xét tg ABC và tg DEC có
BC = CE (gt)
AC = CD (gt)
Góc BCA = góc ECD (đối đỉnh)
=> tg ABC = tg DEC (c-g-c)
b) vì tg ABC = tg DEC (cmt)
=> góc BAC = góc CDE ( góc tương ứng)
Mà góc BAC = 90° (gt)
=> góc CDE = 90°
c) xét tg ACE và tg DCB có:
Góc BCD = góc ACE (đối đỉnh)
AC = CD ( gt)
CE = CB (gt)
=> tg ACE = tg BDC (c-g-c)
=> góc CBD = góc CEA ( góc tương ứng)
Mà hai góc này ở vị trí soi le trong
=> AE // BD
Vì tg ACE = tg BDC (cmt)
=> AE = BD ( cạnh tương ứng)
Đúng 1
Bình luận (0)
Giúp e bài 4 vs ạ(có vẽ hình),e cần cách lm dễ hiểu chi tiết,bài này e cần lắm luôn đó ạ nên giúp e lm đúng vs(nếu mn có thời gian thì giúp e luôn bài 2 vs,e ko đc chắc chắn bài này e lm có đúng ko)e cảm ơn nhìu lắm ạ!!!
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Đúng 1
Bình luận (0)
mn giúp e câu này với, giải chi tiết ra cho e ạ! 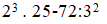
\(=8\cdot25-72:9=200-8=192\)
Đúng 4
Bình luận (0)
Giải chi tiết giúp e vs ạ. Em cần gấp ạ. Cảm ơn nhìu 💞
Xet tam giac BDC va tam giac CEB ta co
^BDC = ^CEB = 900
BC _ chung
^BCD = ^CBE ( gt )
=> tam giac BDC = tam giac CEB ( ch - gn )
=> ^DBC = ^ECB ( 2 goc tuong ung )
Ta co ^B - ^DBC = ^ABD
^C - ^ECB = ^ACE
=> ^ABD = ^ACE
Xet tam giac IBE va tam giac ICD
^ABD = ^ACE ( cmt )
^BIE = ^CID ( doi dinh )
^BEI = ^IDC = 900
Vay tam giac IBE = tam giac ICD (g.g.g)
c, Do BD vuong AC => BD la duong cao
CE vuong BA => CE la duong cao
ma BD giao CE = I => I la truc tam
=> AI la duong cao thu 3
=> AI vuong BC
Đúng 1
Bình luận (0)
Mn ơi giúp e bài này với ạ, e cần gấp lắm. E sắp thi cuối năm r ạ hmu-
\(\dfrac{1}{9+x}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
E cảm ơn mn nhìu lắm!!! Mọng mn giải chi tiết cho e hiểu ạ hyhy XĐ
ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}
Đúng 2
Bình luận (0)
Mn ơi giúp e bài này với ạ, e cần gấp lắm. E sắp thi cuối năm r ạ hmu-
\(\dfrac{x+2}{2019}+\dfrac{x+3}{2018}=\dfrac{x+4}{2017}+\dfrac{x}{2021}\)
E cảm ơn mn nhìu lắm!!! Mọng mn giải chi tiết cho e hiểu ạ hyhy XĐ
Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
Đúng 3
Bình luận (0)
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....
Đúng 2
Bình luận (0)
























