hic cíu mng oi

a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)

b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

1.

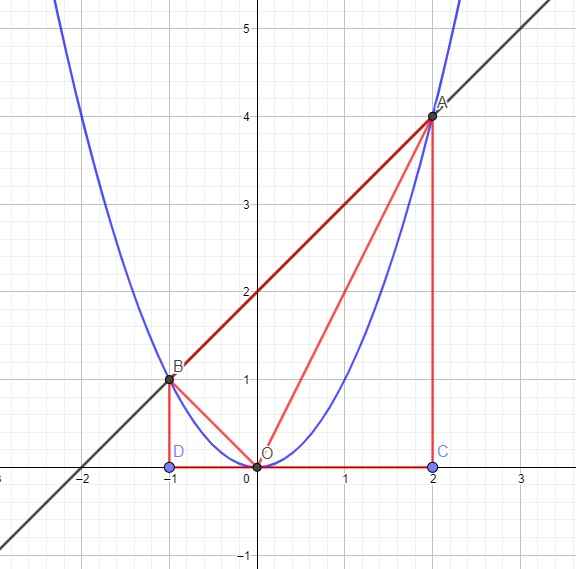
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)

Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)

Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C

Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)

\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)

Ta có:

\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)

\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)

\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)

#include <bits/stdc++.h>

using namespace std;

double a,cv,dt;

int main()

{

cin>>a;

cv=a*4;

dt=a*a;

cout<<fixed<<setprecision(2)<<cv<<endl;

cout<<fixed<<setprecision(2)<<dt;

return 0;

}

28A

Các câu còn lại đúng rồi á bạn

a, bạn tự sắp xếp nhé 

b, Ta có :  \(P\left(x\right)+Q\left(x\right)\)hay 

\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x-2x^5+3x^4-2x^3+4x^2-\dfrac{1}{4}\)

\(=6x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)

Ta có \(P\left(x\right)-Q\left(x\right)\)hay 

\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x+2x^5-3x^4+2x^3-4x^2+\dfrac{1}{4}\)

\(=4x^5-7x^3-6x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)

Giá trị x=0 là nghiệm của P(x) vì ko có hệ số tự do => GT là 0 

Cái còn lại 1/4 là hệ số tự do => x=0 ko phải là nghiệm của Q(x)

c, Ta có : \(Q\left(-1\right)=4+3+2+2-\dfrac{1}{4}=11-\dfrac{1}{4}=\dfrac{43}{4}\)