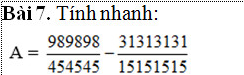
Trình bày chi tiết giúp em với ạ!Em cảm ơn
Giúp em trình bày chi tiết ạ em cảm ơn
\(y=\dfrac{x-1}{x+2}\left(x\ne-2\right)\Rightarrow y'=\dfrac{\left(x+2\right)-\left(x-1\right)}{\left(x+2\right)^2}=\dfrac{3}{\left(x+2\right)^2}\)
Giả sử d là tiếp tuyến cần tìm của đths trên
a. d đi qua \(N\left(-1;-2\right)\) . Suy ra : HSG của d : \(\dfrac{3}{\left(-1+2\right)^2}=3\)
PTTT d : \(y=3\left(x+1\right)-2=3x+1\)
b.d có hđtđ \(x_o=3\) \(\Rightarrow y_o=\dfrac{3-1}{3+2}=\dfrac{2}{5};y'=\dfrac{3}{25}\)
PTTT d : \(y=\dfrac{3}{25}\left(x-3\right)+\dfrac{2}{5}=\dfrac{3x}{25}+\dfrac{1}{25}\)
c. Tung độ tiếp điểm yo = 9 nên : \(\dfrac{x_o-1}{x_o+2}=9\Leftrightarrow x_o=-\dfrac{19}{8}\)
y' = 64/3
PTTT d : \(y=\dfrac{64}{3}\left(x+\dfrac{19}{8}\right)+9=\dfrac{64}{3}x+\dfrac{179}{3}\)
d. Ta có : \(\dfrac{3}{\left(x_o+2\right)^2}=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}x_o+2=3\\x_o+2=-3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x_o=1\\x_o=-5\end{matrix}\right.\)
Với xo = 1 \(\Rightarrow y_o=0\) . PTTT d : y = 1/3(x-1) = 1/3x - 1/3
Với xo = -5 \(\Rightarrow y_o=2\) . PTTT d : \(y=\dfrac{1}{3}\left(x+5\right)+2=\dfrac{1}{3}x+\dfrac{11}{3}\)
Mọi người giúp em trình bày chi tiết (nếu được). Em cảm ơn ạ
giải chi tiết giúp em với ạ, em cảm ơn ^^ Giải bất phương trình sau

ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)
mọi người ơi giải giúp em phương trình này với ạ
3x(2-x)-5 = 1-(3x ngũ 2 + 2)
giải chi tiết giúp em với ạ cảm ơn mọi người nhiều ạ
3x(2-x)-5=1-(3x2+2)
<=>6x-3x2-5=-3x2-2
<=>6x=3
<=>x=1/2
giải phương trình sau: \(\sqrt[3]{2-x}+\sqrt{x-1}=1\) (mn giải chi tiết giúp em với, em cảm ơn ạ)
ĐKXĐ: \(x\ge1\)
Đặt \(\left\{{}\begin{matrix}\sqrt[]{x-1}=a\ge0\\\sqrt[3]{2-x}=b\end{matrix}\right.\) \(\Rightarrow a^2+b^3=1\)
Ta được hệ:
\(\left\{{}\begin{matrix}a+b=1\\a^2+b^3=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=1-a\\a^2+b^3=1\end{matrix}\right.\)
\(\Rightarrow a^2+\left(1-a\right)^3=1\)
\(\Leftrightarrow a^3-4a^2+3a=0\)
\(\Leftrightarrow a\left(a-1\right)\left(a-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=0\\a=1\\a=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt[]{x-1}=0\\\sqrt[]{x-1}=1\\\sqrt[]{x-1}=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=10\end{matrix}\right.\)
Mọi người giúp em câu 1 với ạ trình bày chi tiết giúp em luôn ạ (em đang cần gấp)
Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
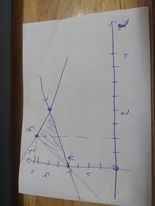
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A

giải chi tiết giúp em với ạ em cảm ơn ạ
a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)
Giải giúp em với ạ không cân chi tiết ạ em cảm ơn 
Giúp em bài này với ạ . Giả chi tiết giúp em luôn nha. Em cảm ơn nhiều ạ
\(\dfrac{2A}{2A+16.5}=\dfrac{43,66}{100}\)
=> \(200A=43,66.\left(2A+16.5\right)\)
=> \(200A-87,32A=3492,8\)
=> \(112,68A=3492,8\)
=> A= 31