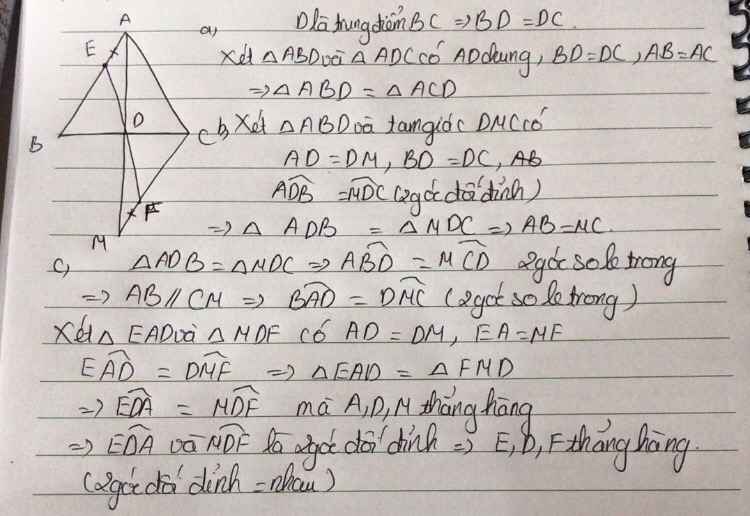cho tam giác abc cân tại a. trên tia đối bc lấy d. trên tia đối cb lấy e sao cho cd=be. a) chứng minh góc adb = góc ace

Những câu hỏi liên quan
Câu 3: (3 điểm) Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD.
a) Chứng minh: AD = BC.
b) Gọi E là giao điểm AD và BC. Chứng minh: Δ EAC = Δ EBD
c) Chứng minh: OE là phân giác của góc xOy.
Xem chi tiết

a) Ta có:
OC = OA + AC
OD = OB + BD
Mà OA = OB (gt)
AC = BD (gt)
\(\Rightarrow\) OC = OD
Xét \(\Delta OAD\) và \(\Delta OBC\) có:
\(\widehat{O}\) chung
OA = OB (gt)
OD = OC (cmt)
\(\Rightarrow\Delta OAD=\Delta OBC\) (c-g-c)
\(\Rightarrow AD=BC\) (hai cạnh tương ứng)
Đúng 1
Bình luận (0)
b) Do \(\Delta OAD=\Delta OBC\) (cmt)
\(\Rightarrow\widehat{BDE}=\widehat{ACE}\) (hai góc tương ứng)
\(\widehat{OAD}=\widehat{OBC}\) (hai góc tương ứng)
Mà \(\widehat{EAC}+\widehat{OAD}=180^0\) (kề bù)
\(\widehat{EBD}+\widehat{OBC}=180^0\) (kề bù)
\(\Rightarrow\widehat{EAC}=\widehat{EBD}\)
Xét \(\Delta EAC\) và \(\Delta EBD\) có:
\(\widehat{EAC}=\widehat{EBD}\) (cmt)
AC = BC (gt)
\(\widehat{ACE}=\widehat{BDE}\) (cmt)
\(\Rightarrow\Delta EAC=\Delta EBD\) (g-c-g)
Đúng 0
Bình luận (0)
b) Do \(\Delta OAD=\Delta OBC\) (cmt)
\(\Rightarrow\widehat{BDE}=\widehat{ACE}\) (hai góc tương ứng)
\(\widehat{OAD}=\widehat{OBC}\) (hai góc tương ứng)
Mà \(\widehat{EAC}+\widehat{OAD}=180^0\) (kề bù)
\(\widehat{EBD}+\widehat{OBC}=180^0\) (kề bù)
\(\Rightarrow\widehat{EAC}=\widehat{EBD}\)
Xét \(\Delta EAC\) và \(\Delta EBD\) có:
\(\widehat{EAC}=\widehat{EBD}\) (cmt)
AC = BC (gt)
\(\widehat{ACE}=\widehat{BDE}\) (cmt)
\(\Rightarrow\Delta EAC=\Delta EBD\) (g-c-g)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho ABC vuông tại A và.Tia phân giác góc C cắt AB tại M. Kẻ ME ⊥ BC ( E∈ BC).a) Chứng minh AM MEb) ABE là tam giác gì? Vì sao?c) Gọi CA cắt EM tại F. Chứng minh BF 2.AEd) Gọi CM cắt BF tại Q, kẻ AH ⊥BC ( H∈ BC).Trên tia AH lấy điểm D sao cho H là trung điểm của AD. Chứng minh E là trung điểm của QD và QF2 BC2 – 4. AH2Thanks mng!
Đọc tiếp
Cho ABC vuông tại A và.Tia phân giác góc C cắt AB tại M. Kẻ ME ⊥ BC ( E∈ BC).
a) Chứng minh AM = MEb) ABE là tam giác gì? Vì sao?
c) Gọi CA cắt EM tại F. Chứng minh BF = 2.AE
d) Gọi CM cắt BF tại Q, kẻ AH ⊥BC ( H∈ BC).Trên tia AH lấy điểm D sao cho H là trung điểm của AD. Chứng minh E là trung điểm của QD và QF2 = BC2 – 4. AH2
Thanks mng!
Cho ∆ ABC cân (AB AC) Trên tia đối cua tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD CE. Chứng minh:a/ AB ADb) ∆𝐴𝐵𝐷 ∆𝐴𝐶𝐸c/Kẻ trung tuyến AM của tam giác ABC . Cminh AM cũng là đường trung tuyến của tam giác ADEd) Vẽ BH vuông góc với AD( H ϵ AD), vẽ CK vuông góc với AE( K ϵ AE).Chứng minh :BHCKe)Tia HB cắt tia KC tại I. Chứng minh AI là tia phân giác của góc BACf)C/minh : HK // DE
Đọc tiếp
Cho ∆ ABC cân (AB =AC) Trên tia đối cua tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh:
a/ AB< AD
b) ∆𝐴𝐵𝐷 = ∆𝐴𝐶𝐸
c/Kẻ trung tuyến AM của tam giác ABC . Cminh AM cũng là đường trung tuyến của tam giác ADE
d) Vẽ BH vuông góc với AD( H ϵ AD), vẽ CK vuông góc với AE( K ϵ AE).
Chứng minh :BH=CK
e)Tia HB cắt tia KC tại I. Chứng minh AI là tia phân giác của góc BAC
f)C/minh : HK // DE
a: ΔABC cân tại A nên góc ABC<90 độ
=>góc ABD>90 độ
=>AB<AD
b: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
c: MB+BD=MD
MC+CE=ME
mà MB=MC và BD=CE
nên MD=ME
=>M là trung điểm của DE
=>AM là đường trung tuyến của ΔADE
d: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
=>ΔAHB=ΔAKC
=>HB=KC
f: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
Đúng 0
Bình luận (0)
Cho ∆ABC có AB=AC. Tia phân giác góc A cắt cạnh BC tại D. a) Chứng minh: ∆ABD=∆ACD ; AD vuông góc với BC. b) Trên nửa mặt phẳng bờ AB chứa điểm C,vẽ Ax//BC. Chứng ming : góc ABC bằng góc CAx. c) Trên tia Ax lấy điểm K sao cho AK=BD. Gọi I là trung điểm của AC. Chứng minh I là trung điểm của DK.
a: Xét ΔBAD và ΔCAD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, AB<AC. lấy điểm D sao cho A là trung điểm của BD
a) chứng minh CA là tia phân giác của góc BCD
b) vẽ BE vuông góc với CD tại E, BE cắt CA tại I. Vẽ IF vuông góc với CB tại F. chứng minh tam giác CEF cân và EF song song với DB
c) so sánh IE và IB
d) tìm điều kiện của tam giác DBC để tam giác BEF cân tại F
a: Xet ΔCBD có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
=>CA là phân giác củagóc BCD
b: Xét ΔCEI vuông tại E và ΔCFI vuông tại F có
CI chung
góc ECI=góc FCI
=>ΔCEI=ΔCFI
=>CE=CF
=>ΔCEF cân tạiC
Xet ΔCDB có CE/CD=CF/CB
nên EF//DB
c: IE=IF
IF<IB
=>IE<IB
Đúng 0
Bình luận (0)
Cho Tam Giác ABC đều kẻ Ah vuông góc với BC tại H. Trên tia đối của tia BC lấy điểm E sao cho BEBC. Trên tia đối của tia CB lấy điểm D Sao cho CBCD.A, Chứng minh rằng tam giác AEBADCb, Từ D kẻ DF vuông góc với AC tại F. Chứng minh rằng tam giác CHF cânc, Chứng minh rằng AD//HFd, Từ B kẻ Bm Vuông góc AE tại M, Từ C kẻ CN vuông góc với AD tại N. Gọi I là giao điểm của Bm và Cn . Chứng Minh AI là phân giác của góc BAC.
Đọc tiếp
Cho Tam Giác ABC đều kẻ Ah vuông góc với BC tại H. Trên tia đối của tia BC lấy điểm E sao cho BE=BC. Trên tia đối của tia CB lấy điểm D Sao cho CB=CD.
A, Chứng minh rằng tam giác AEB=ADC
b, Từ D kẻ DF vuông góc với AC tại F. Chứng minh rằng tam giác CHF cân
c, Chứng minh rằng AD//HF
d, Từ B kẻ Bm Vuông góc AE tại M, Từ C kẻ CN vuông góc với AD tại N. Gọi I là giao điểm của Bm và Cn . Chứng Minh AI là phân giác của góc BAC.
Cho tam giác ABC, đường cao AH.Trên nửa mặt phẳng chứa A bờ CB lấy các điểm D và E sao cho tam giác ABD và ACE vuông can tại B và C. Trên tia đối của tia AH lấy K sao cho AK=BC. CMR:
a.Tam giác ABK=Tam giác BCD
b.CD vuông góc BK, BE vuông góc CK
c.Ba đường AH,BE,CD đồng quy
Cho tam giác ABC có AB = AC, D là trung điểm của BC.
a.) Chứng minh: ΔABD = ΔACD
b.) Trên tia AD lấy điểm M sao cho AD = DM.
Chứng minh AB = MC
c.) Kẻ DE vuông góc với AB tại E, kẻ DF vuông góc với MC tại F. Chứng minh E, D, F thẳng hàng.
Vẽ hình ra giùm mik luôn nha, cho mình cảm ơn
Cho tam giác ABC vuông tại A (AB < AC). Vẽ AH ⊥ BC (H ∈ BC). Lấy điểm K trên tia HC sao cho: HK = BH. Qua K kẻ đường thẳng vuông góc với AC tại I (I ∈ AC), đường thẳng đó cắt tia AH tại E
a) Chứng minh ∆ AHB = ∆ AHK; b) Chứng minh: EI // AB;
c) Chứng minh: AH = HE
d) Lấy điểm D trên đoạn CE sao cho CD = CI. Chứng minh 3 điểm A, K, D thẳng hàng.
a: Xét ΔAHB vuông tại H và ΔAHK vuông tại H có
AH chung
HB=HK
Do đó: ΔAHB=ΔAHK
Đúng 0
Bình luận (0)