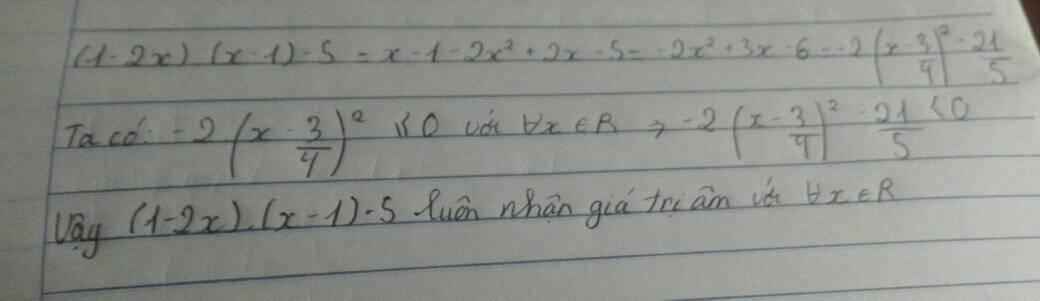(1-2x)(x-1)-5

=-2x²+3x-1-5

=-2x²+3x-6

=-2(x²-3/2x+3)

=-2(x-3/4)²-39/8

Vì (x-3/4)²≥0  với mọi x

⇒-2(x-3/4)²≤0

⇒-2(x-3/4)²-39/8<0

Vậy biểu thức (1-2x)(x-1)-5 luôn âm với mọi x

Câu trả lời bằng hình ảnh.

\(\frac{x+3}{x+5}< 0\)

\(\Rightarrow\)x+3 và x+5 trái dấu

Mà \(x+3< x+5\)

\(\Rightarrow\hept{\begin{cases}x+3< 0\\x+5>0\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x< -3\\x>-5\end{cases}}\)

\(\Rightarrow-3>x>-5\)

Do đó x=-4

A hay D cũng đc, cái nào cũng giống nhau

Chọn A

\(a,P=5x\left(2-x\right)-\left(x+1\right)\left(x+9\right)\)

\(=10x-5x^2-\left(x^2+x+9x+9\right)\)

\(=10x-5x^2-x^2-x-9x-9\)

\(=\left(10x-x-9x\right)+\left(-5x^2-x^2\right)-9\)

\(=-6x^2-9\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow-6x^2\le0\forall x\)

\(\Rightarrow-6x^2-9\le-9< 0\forall x\)

hay \(P\) luôn nhận giá trị âm với mọi giá trị của biến \(x\).

\(b,Q=3x^2+x\left(x-4y\right)-2x\left(6-2y\right)+12x+1\)

\(=3x^2+x^2-4xy-12x+4xy+12x+1\)

\(=\left(3x^2+x^2\right)+\left(-4xy+4xy\right)+\left(-12x+12x\right)+1\)

\(=4x^2+1\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow4x^2\ge0\forall x\)

\(\Rightarrow4x^2+1\ge1>0\forall x\)

hay \(Q\) luôn nhận giá trị dương với mọi giá trị của biến \(x\) và \(y\).

#\(Toru\)

Bài 1 :

Để \(x^2+5x-x^2\)

\(\Leftrightarrow5>-x^2+x\)

Bài 1) Chứng minh rằng các biểu thức sau luôn có giá trị âm với mọi giá trị của biến: 
a) 9x^2+12x-15 
=-(9x^2-12x+4+11) 
=-[(3x-2)^2+11] 
=-(3x-2)^2 - 11. 
Vì (3x-2)^2 không âm với mọi x suy ra -(3x-2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x 
Do đó -[(3*x)-2]^2-11 < 0 với mọi giá trị của x. 
Hay -9*x^2 + 12*x -15 < 0 với mọi giá trị của x. 

b) -5 – (x-1)*(x+2) 
= -5-(x^2+x-2) 
=-5- (x^2+2x.1/2 +1/4 - 1/4-2) 
=-5-[(x-1/2)^2 -9/4] 
=-5-(x-1/2)^2 +9/4 
=-11/4 - (x-1/2)^2 
Vì (x-1/2)^2 không âm với mọi x suy ra -(x-1/2)^2 nhỏ hơn hoặc bằng 0 vơi mọi x 
Do đó -11/4 - (x-1/2)^2 < 0 với mọi giá trị của x. 
Hay -5 – (x-1)*(x+2) < 0 với mọi giá trị của x. 

Bài 2) 
a) x^4+x^2+2 
Vì x^4 +x^2 lớn hơn hoặc bằng 0 vơi mọi x 
suy ra x^4+x^2+2 >=2 
Hay x^4+x^2+2 luôn dương với mọi x. 

b) (x+3)*(x-11) + 2003 
= x^2-8x-33 +2003 
=x^2-8x+16b + 1954 
=(x-4)^2 + 1954 >=1954 
Vậy biểu thức luôn có giá trị dương với mọi giá trị của biến

bị ''rảnh'' ak ? 

tự hỏi r tự trả lời

1/ \(-9x^2+12x-15=\left(-9x^2+2.2.3x-4\right)-11\)

\(=-11-\left(3x-2\right)^2\le-11< 0\)

Câu b và câu 2 tương tự

3L = -x² + 6x - 15

= -(x - 3)² - 6

=> L = \(\frac{-\left(x-3\right)^2}{3}-2\le-2\) \(\forall x\)