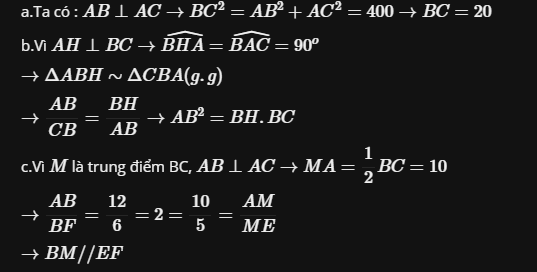Cho tam giác ABC vuông tại A, đường cao AH, biết AB=10m, BH=5cm. Chứng minh rằng tan B=3tan C

Những câu hỏi liên quan
CHO TAM GIÁC ABC VUÔNG TẠI A, ĐƯỜNG CAO AH, BIẾT AB=10cm, BH=5cm. CMR: tan B= 3tan C
Cho tam giác ABC vuông tại A, đường cao AH, biết AB =5cm AC =12cm a) tính BC và góc B b) chứng minh rằng: AB².CH=AC².BH
a.
Xét tam giác ABC vuông tại A, có:
AB^2 + AC^2 = BC^2 (Định Lý Pytago) => BC^2 = 25+144 = 169
=> BC = 13 (cm)
sinB = AC/BC = 12/13 => B = 67.4 (độ)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB=5cm AC=12cm . vẽ đường cao AH a. Chứng minh tam giác HBA đồng dạng tam Giác ABC b tính AH,BH
Hình vẽ:
Giải
a. Xét ΔHBA và ΔABC có:
\(\widehat{B}\) chung
\(\widehat{BHA}=\widehat{BAC}=90^0\)
⇒ΔHBA ∼ ΔABC (g.g)
b. Xét ΔABC vuông tại A có:
\(BC^2=AB^2+AC^2\)(định lí py-ta-go)
\(=5^2+12^2\)
\(=169\)
\(\rightarrow BC=\sqrt{169}=13\left(cm\right)\)
Vì ΔABC ∼ ΔHBA (cmt)
\(\rightarrow\dfrac{AB}{BH}=\dfrac{AC}{AH}=\dfrac{BC}{AB}hay\dfrac{5}{BH}=\dfrac{12}{AH}=\dfrac{13}{5}\)
⇒\(BH=\dfrac{5.5}{13}=\dfrac{25}{13}\left(cm\right)\)
⇒\(AH=\dfrac{12.5}{13}=\dfrac{60}{13}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH. Biết AB = 5cm, BC = 6cm.
a) Tính độ dài các đoạn thẳng BH, AH.
b) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng ba điểm A, G, H thẳng hàng.
c) Chứng minh: góc ABG = góc ACM.
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH = 5cm. Biết CH = 6cm. tính:
a) AB, AC,BC và BH?
b) Diện tích tam giác ABC
Bài2: Cho tam giác ABC vuông tại A, đường cao AH; AB = 15cm; BC = 25cm. BTính:
a) AC,AH, HC và BH?
b) Diện tích tam giác ABC
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
Đúng 3
Bình luận (0)
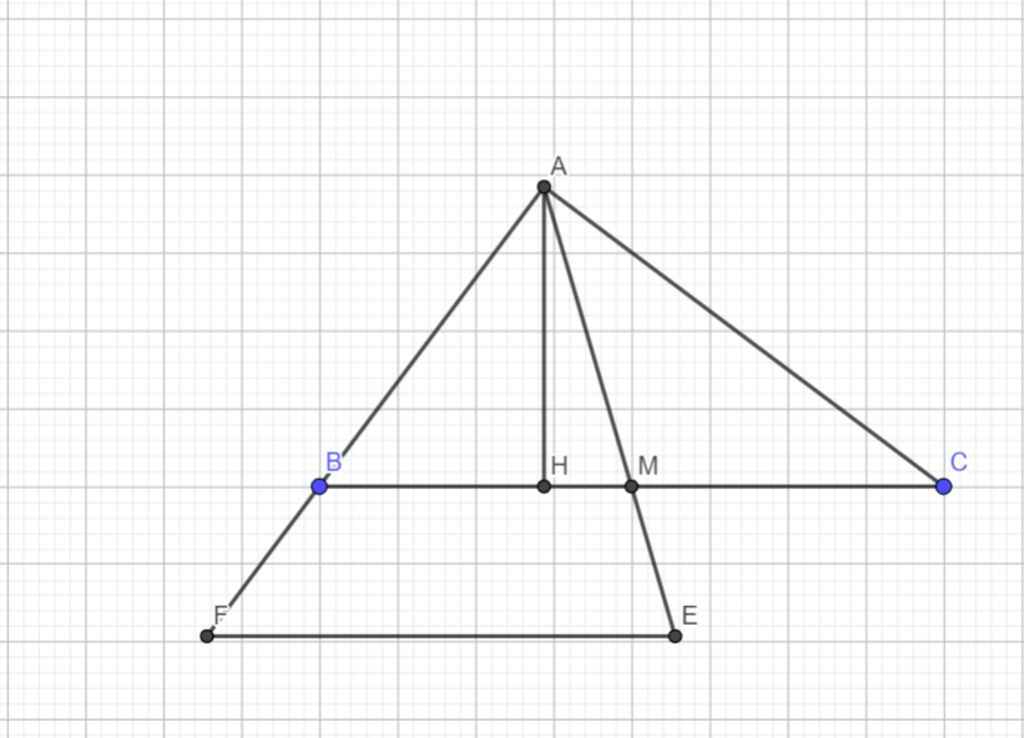
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 12cm, AC 16cm. a) Tính độ dài BC b) Chứng minh rằng: AB2 BH. BC c) Vẽ trung tuyến AM của DABC, trên tia đối tia MA lấy điểm E sao cho ME 5cm, trên tia đối của tia BA lấy điểm F sao cho BF 6cm. CMR: BC // EF
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, AC = 16cm.
a) Tính độ dài BC
b) Chứng minh rằng: AB2 = BH. BC
c) Vẽ trung tuyến AM của DABC, trên tia đối tia MA lấy điểm E sao cho ME = 5cm, trên
tia đối của tia BA lấy điểm F sao cho BF = 6cm.
CMR: BC // EF
Áp dụng định lý pytago ta có :
`AC^2+AB^2=BC^2`
hay `16^2+12^2=BC^2`
`=>BC^2=400`
`=>BC=20(cm)`
Đúng 1
Bình luận (1)
Bài 1 : Cho tam giác ABC cân tại A đường cao AH . Biết AB5cm , BC6cma) tính độ dài các đoạn thẳng AH , BHb) Gọi G là trọng tâm của tam giác ABC Chứng minh rằng ba điểm A , G , H thẳng hàngc) Chứng minh góc ABG ACG Bài 2 : Cho tam giác ABC cân tại A . Gọi M là trung điểm của cạnh BCa) chứng minh tam giác ABM ACMb) Từ M vẽ MH vuông góc AB và MK vuông góc AC . Chứng Minh BH CKc) Từ B vẽ BP vuông góc với AC , BP cắt MH tại I , Chứng minh tam giác IBM cân
Đọc tiếp
Bài 1 : Cho tam giác ABC cân tại A đường cao AH . Biết AB=5cm , BC=6cm
a) tính độ dài các đoạn thẳng AH , BH
b) Gọi G là trọng tâm của tam giác ABC Chứng minh rằng ba điểm A , G , H thẳng hàng
c) Chứng minh góc ABG = ACG
Bài 2 : Cho tam giác ABC cân tại A . Gọi M là trung điểm của cạnh BC
a) chứng minh tam giác ABM = ACM
b) Từ M vẽ MH vuông góc AB và MK vuông góc AC . Chứng Minh BH = CK
c) Từ B vẽ BP vuông góc với AC , BP cắt MH tại I , Chứng minh tam giác IBM cân
Bài 1:Cho góc xOy có Oz là tia phân giác,M là điểm bất kì thuộc tia Oz.Qua M kẻ đường thẳng a vuông góc với Ox tại A cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B cắt tia Ox tại D.
a,CM tam giác AOM bằng tam giác BOM từ đó suy ra OM là đường trung trực của đoạn thẳng AB
b,Tam giác DMC là tam giác gì?Vì sao?
c,CM DM + AM < DC
Bài 2:Cho tam giác ABC có góc A=90* và đường phân giác BH(H thuộc AC).Kẻ HM vuông góc với BC(M thuộc BC).Gọi N là giao điểm của AB và MH.CM:
a, Tam giác ABGH bằng tam giác MBH.
b, BH là đường trung trực của đoạn thẳng AH
c, AM // CN
d, BH vuông góc với CN
Bài 3:Cho tam giác ABC vuông góc tại C có góc A = 60* và đường phân giác của góc BAC cắt BC tại E.Kẻ EK vuông góc với BK tại K(K thuộc AB).Kẻ BD vuông góc với AE tại D(D thuộc AE).CM:
a, Tam giác ACE bằng tam giác AKE
b, BE là đường trung trực của đoạn thẳng CK
c, KA=KB
d, EB>EC
Bài 4:Cho tam giác ABC vuông tại A có đường phân giác của góc ABC cắt AC tại E.Kẻ EH vuông góc BC tại H(H thuộc BC).CM:
a, Tam giác ABE bằng tam giác HBE
b, BE là đường trung trực của đoạn thẳng AH
c, EC > AE
Bài 5:Cho tam giác ABC vuông tại A có đường cao AH
1,Biết AH=4cm,HB=2cm,Hc=8cm:
a,Tính độ dài cạnh AB,AC
b,CM góc B > góc C
2,Giả sử khoảng cách từ điểm A đến đường thẳng chứa cạnh BC là không đổi.Tam giác ABC cần thêm điều kiện gì để khoảng cách BC là nhỏ nhất.
Bài 6:Cho tam giác ABC vuông tại A có đường cao AH.Trên cạnh BC lấy điểm D sao cho BD=BA.
a,CM góc BAD= góc BDA
b,CM góc HAD+góc BDA=góc DAC+góc DAB.Từ đó suy ra AD là tia phân giác của góc HAC
c,Vẽ DK vuông góc AC.Cm AK=AH
d,Cm AB+AC<BC+AH
Bài 7:Cho tam giac ABC vuông tại C.Trên cạnh AB lấy điểm D sao cho AD = AC.kẻ qua D đường thẳng vuông góc với AB cắt BC tại E. AE cắt CD tại I.
a,CM AE là phân giác \{CAB}
b,CM AE là trung trực của CD
c,So sánh CD và BC
d,M là trung điểm của BC,DM cắt BI tại G,CG cắt DB tại K.CM K là trung điểm của DB
Bài 8:Cho tam giác ABC có BC=2AB.Gọi M là trung điểm của BC,N là trung điểm của BM.Trên tia đối của NA lấy điểm E sao cho AN=EN.CM:
a,Tam giác NAB=Tam giác NEM
b,Tam giác MAB là tam giác cân
c,M là trọng tâm của Tam giác AEC
d,AB>\frac{2}{3}AN
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH a. Chứng minh tam giác ABC đồng dạng tam giác HBA b. Cho biết BH =2cm, BC =6cm.tính AB c. Đường phân giác của góc B cắt AH tại I.chứng minh IA×AH=IH×AC
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{B}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A, đường cao AH.
a) Chứng minh tam giác ABC đồng dạng với tam giác HBA, từ đó suy ra AB.AH = BH.AC
b) Tia phân giác của góc ABC cắt AH tại I. Biết BH = 3cm, AB = 5cm. Tính AI,HI
c) Tia phân giác góc HAC cắt BC tại K. Chứng minh IK // AC
tự kẻ hình
a, xét tam giác ABC và tam giác HBA có : góc B chung
góc BAC = góc BHA = 90
=> tam giác ABC đồng dạng với tam giác HBA (g-g)
=> AB/BH = AC/AH
=> AB.AH = BH.AC
b, xét tam giác BAH vuông tại H => HB^2 + HA^2 = AB^2 (Pytago)
BH = 3; AB = 5(gt)
=> 3^2 + AH^2 = 5^2
=> AH^2 = 16
=> AH = 4 do AH > 0
xét tam giác ABH có : BI là pg của góc ABH (gt)
=> AI/AB = IH/BH (tính chất)
=> AI+IH/AB+BH = AI/AB = IH/BH
=> AH/AB + BH = AI/AB = IH/BH
có: AH = 4; AB = 5; BH = 3
=> 4/3+5 = AI/5 = IH/3
=> AI/5 = IH/3 = 1/2
=> AI = 5/2 và IH = 3/2
c, góc CAH = 90 - góc HAB
góc HBA = 90 - góc HAB
=> góc CAH = góc HBA
xét tam giác AHC và tam giác BHA có: góc AHC = góc BHA = 90
=> tam giác AHC đồng dạng với tam giác BHA (g-g)
=> AC/AB = AH/HB
=> AC/AH = AB/HB
BI là pg của tam giác AHB => AI/AH = AB/AB
CK là pg của tam giác AHC => CK/KH = AC/AH
=> AI/AH = CK/KH
=> KI // AC
Xem thêm câu trả lời