Bài 32, 33 ạ ;-;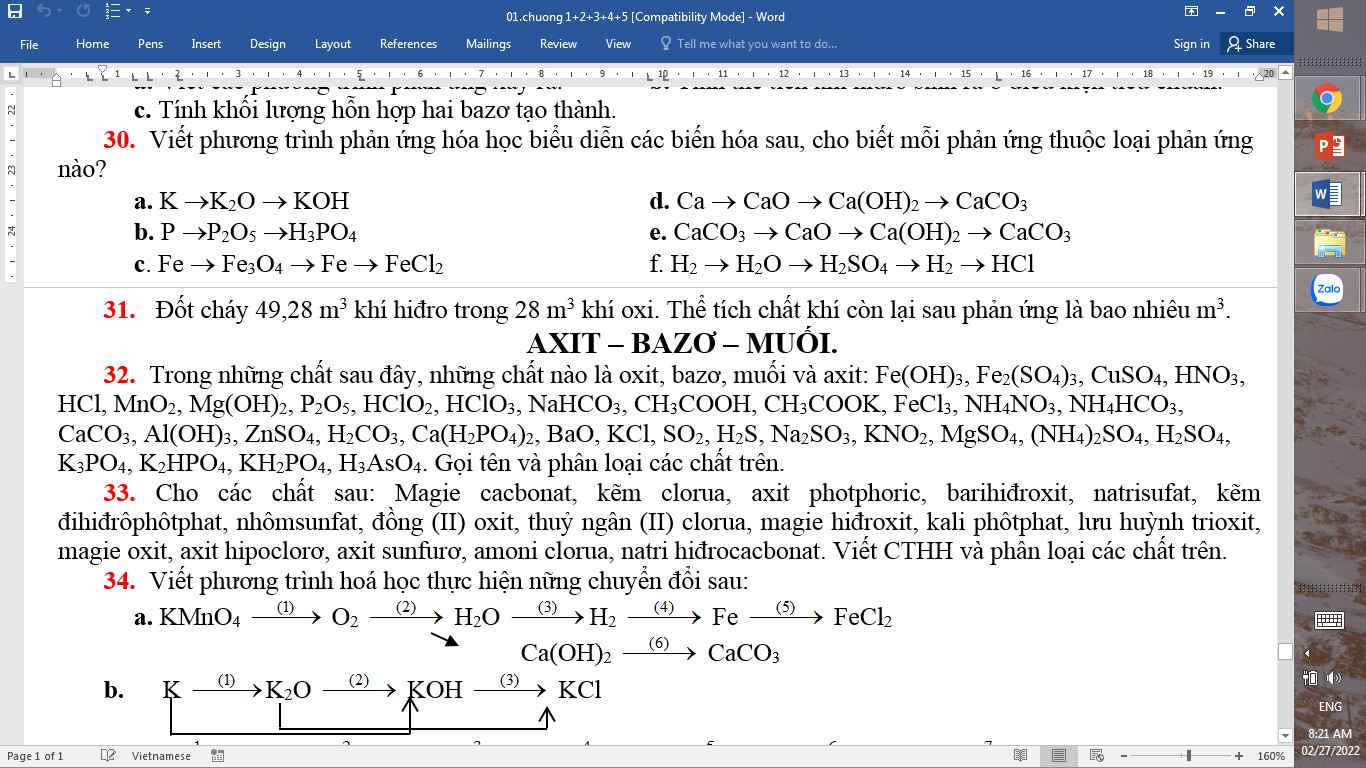

Những câu hỏi liên quan
Chỉ cho mình bài này đi ạ :")
Cho B = 3 + 32 + 33 + …… + 360. Hãy chứng tỏ B chia hết cho 13?
b) B\(=\)(3+32+33)+...+(358+359+360)
\(=\)30(3+32+33)+...+357(358+359+360)
\(=\)3+32+33(30+33+36+...+357)
\(=\)39(30+33+36+...+357)⋮13
⇒ B⋮13
Bài 1: tính tổng dãy số sau:A 1+3+32+33+...+399+3100Các bạn xem bài giải của mình nếu đúng tick cho mình nhé!GiảiTa có: 3A 3.(1+3+32+33+...+399+3100)(1+3+32+33+...+399+3100)3A 3+32+33+...+3100+31013+32+33+...+3100+3101Suy ra: 3A – A (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)(3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)2A 3101−13101−1⇒⇒ A 3101−123101−12Vậy A 3101−12
Đọc tiếp
Bài 1: tính tổng dãy số sau:
A = 1+3+32+33+...+399+3100
Các bạn xem bài giải của mình nếu đúng tick cho mình nhé!
Giải
Ta có: 3A = 3.(1+3+32+33+...+399+3100)(1+3+32+33+...+399+3100)
3A = 3+32+33+...+3100+31013+32+33+...+3100+3101
Suy ra: 3A – A = (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)(3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)
2A = 3101−13101−1
⇒⇒ A = 3101−123101−12
Vậy A = 3101−12
xin lỗi bài trên của mình làm sai
Đúng 0
Bình luận (0)
Ta có: 3A = 3.(1+3+32+33+...+399+3100)
3A = 3+32+33+...+3100+3101
Suy ra: 3A – A = (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)
2A = 3101−1
⇒ A = 3101−1
2
Vậy A = 3101−1
2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
F = 1 + 31 + 32 + 33 + ... + 3100
ai giúp với ạ
\(F=1+3^1+3^2+...+3^{100}\)
\(\Rightarrow3F=3+3^2+...+3^{101}\)
\(\Rightarrow2F=3F-F=3+3^2+...+3^{101}-1-3^1-...-3^{100}=3^{101}-1\)
\(\Rightarrow F=\dfrac{3^{101}-1}{2}\)
Đúng 0
Bình luận (0)
\(3\cdot F=3^1+3^2+...+3^{101}\)
hay \(F=\dfrac{3^{101}-1}{2}\)
Đúng 0
Bình luận (0)
Bài 3:Tìm x∈N biết:
a) 70-5(x-3)=45 b) (2x-1)4 =3.62 -27
c) 3x3 +43=102 -33 d) 3x+2 + 3x =2430
e)24.x-32.x=145-255:51
Mn bày e gấp.Em đag cần gấp ạ
a) 70 - 5(x - 3 ) = 45
5( x - 3 ) = 70 - 45 = 25
x - 3 = 25 : 5 = 5
x = 5 + 3 = 8
b) (2x - 1 )4 = 3 . 62 - 27
(2x - 1 )4 = 3 . 36 - 27
(2x - 1 )4 = 81
Ta thấy 81 = 34 vậy suy ra (2x - 1)4 = 34
Để vế trong ngoặc tròn (2x - 1 ) = 3 thì x cần bằng 2
Thử lại : 2 . 2 - 1 = 4 - 1 = 3
Vậy x = 2
c) 3x3 + 43 = 102 - 33
3x3 + 43 = 100 - 33 = 67
3x3 = 67 + 43 = 110 ( Đoạn này đề bài sai hay tao sai z :)?)
Đúng 0
Bình luận (0)
Ai đó giúp mình với ạ.
3 + 32 + 33+...+3100
\(3A=3^2+3^3+...+3^{101}\)
=>\(A=\dfrac{3^{101}-3}{2}\)
Đúng 0
Bình luận (0)
Giải hộ mình câu này với ạ :
Cho A = 1+32+33+…+3101
`#3107.101107`
`A = 1+ 3 + 3^2+3^3+…+3^101?`
`= (1 + 3 + 3^2) + (3^3 + 3^4 + 3^5) + ... + (3^99 + 3^100 + 3^101)`
`= (1 + 3 + 3^2) + 3^3 * (1 + 3 + 3^2) + ... + 3^99 * (1 + 3 + 3^2)`
`= (1 + 3 + 3^2) * (1 + 3^3 + ... + 3^99)`
`= 13 * (1 + 3^3 + ... + 3^99)`
Vì `13 * (1 + 3^3 + ... + 3^99) \vdots 13`
`=> A \vdots 13`
Vậy, `A \vdots 13.`
Đúng 3
Bình luận (0)
B = 31+ 32 +33 +....+ 3100
gúp mình bài này
bài 1 tính thuận tiênj
a) 13.65+35.12
b)31+32+33+...+39-21-22-...-29
c)3-8*27+4*33*6+40*2*12
ai giup vs mk tak 5 saoooo VÀ 20 XU TL 3 BÀI MS NHẤT
Đúng 0
Bình luận (0)
a: \(13\cdot65+35\cdot12\)
\(=13\cdot65+35\cdot13-35\)
=1300-35
=1265
Đúng 0
Bình luận (0)
a) Cho A = 1 + 3 + 32 + 33 + ... + 32016 . Tìm số dư khi chia A cho 65 .
Giúp em với ạ ![]()
Lời giải:
$A=1+(3+3^2+3^3)+(3^4+3^5+3^6)+....+(3^{2014}+3^{2015}+3^{2016})$
$=1+3(1+3+3^2)+3^4(1+3+3^2)+...+3^{2014}(1+3+3^2)$
$=1+3.13+3^4.13+....+3^{2014}.13$
$=1+13(3+3^4+...+3^{2014})$
$\Rightarrow A-1\vdots 13(1)$
Mặt khác:
$A=1+(3+3^2+3^3+3^4)+....+(3^{2013}+3^{2014}+3^{2015}+3^{2016})$
$=1+3(1+3+3^2+3^3)+....+3^{2013}(1+3+3^2+3^3)$
$=1+(3+...+3^{2013})(1+3+3^2+3^3)$
$=1+40(3+....+3^{2013})$
$\Rightarrow A-1\vdots 5(2)$
Từ $(1); (2)$ mà $(5,13)=1$ nên $A-1\vdots (5.13)$ hay $A-1\vdots 65$
$\Rightarrow A$ chia $65$ dư $1$
Đúng 1
Bình luận (1)




















