Giúp e bài 5 với 

Những câu hỏi liên quan
giúp e bài 5 đến bài 8 với ạ,e cảm ơn
Bài 7:
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔHAC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1), (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 1
Bình luận (0)
Giúp e bài 5 với ạ
Giúp e bài 5 này với ạ
các bác giúp e bài 4 và 5 với e cảm ơn nhiều lắm ạ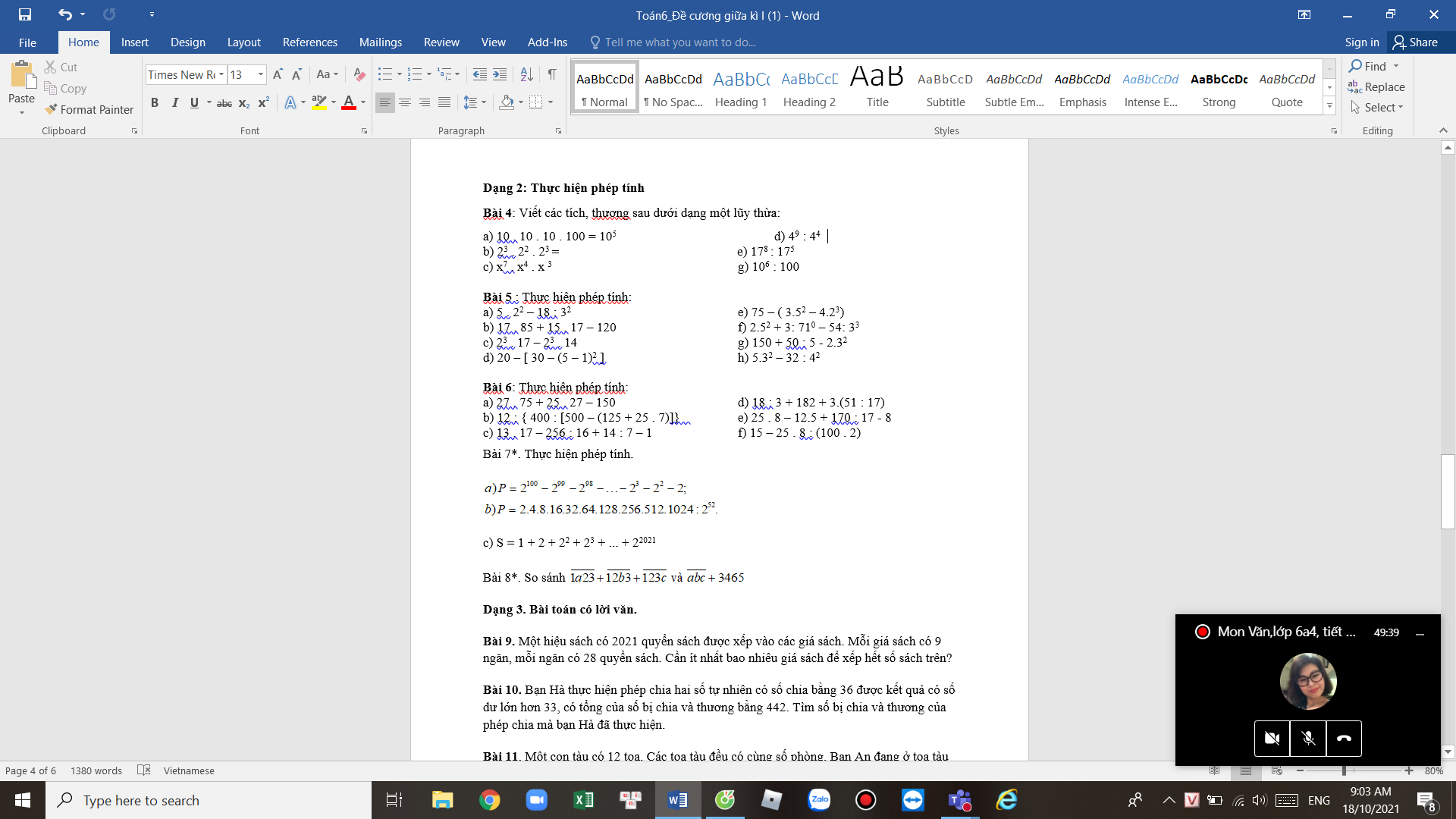
Hình bé quá, em đăng tách ra từng bài một nhé!
Đúng 1
Bình luận (0)
6x²+xy-7x-2y²+7y-5 Giúp e với ạ . (Ai có mẹo lm mấy bài này chia sẻ với e với ạ :((( )
\(6x^2+xy-7x-2y^2+7y-5=-\left(y-2x-1\right)\left(2y+3x-5\right)\)
Đúng 1
Bình luận (0)
\(6x^2+xy-7x-2y^2+7y-5=-2y\left(y-2x-1\right)-3x\left(y-2x-1\right)+5\left(y-2x-1\right)=-\left(y-2x-1\right)\left(2y+3x-5\right)\)
Đúng 1
Bình luận (0)
\(6x^2+xy-7x-2y^2+7y-5\)
\(=\left(2y+3x-5\right)\cdot\left(-y+2x+1\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp e câu b bài 5 với ạ. Cần rất gấp
 mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
Bài 4:
a) Thay x=49 vào B ta có:
\(B=\dfrac{1-\sqrt{49}}{1+\sqrt{49}}=-\dfrac{3}{4}\)
b) \(A=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(A=\left[\dfrac{15-\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right]\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}-5}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}+1}\)
c) Ta có:
\(M=A-B=\dfrac{1}{\sqrt{x}+1}-\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{1-1+\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}+1-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}=1-\dfrac{1}{\sqrt{x}+1}\)
Mà M nguyên khi:
\(1\) ⋮ \(\sqrt{x}+1\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;-1\right\}\)
Mà: \(\sqrt{x}+1\ge1\)
\(\Rightarrow\sqrt{x}+1=1\)
\(\Rightarrow\sqrt{x}=0\)
\(\Rightarrow x=0\left(tm\right)\)
Vậy M nguyên khi x=0
Đúng 1
Bình luận (0)
Thầy cô giúp e với, bài 2 thôi ạ, giúp e với e đang cần gấp 
2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được
Đúng 2
Bình luận (0)
Giúp e 3 bài này gấp với ạ. Phiền mn giúp e với ạ. E cảm ơn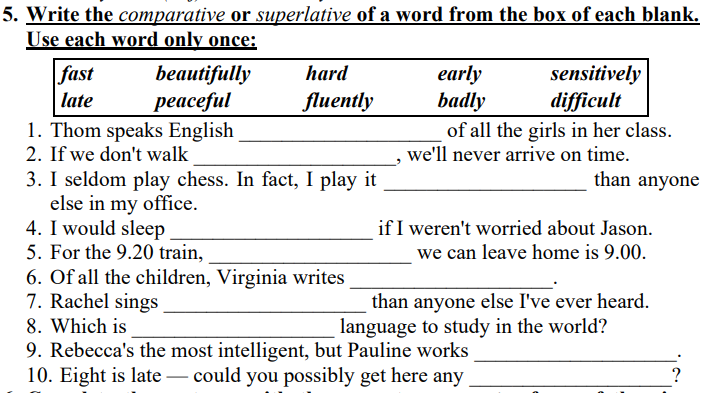
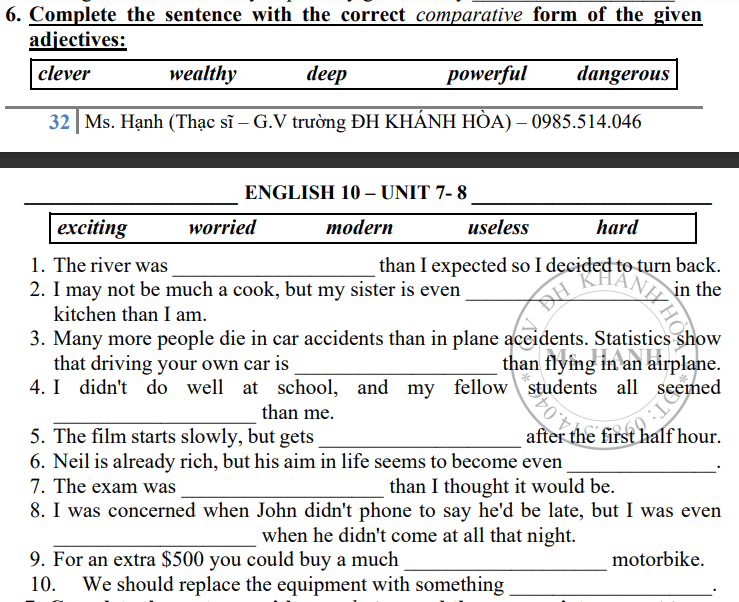

bạn đăng tách ra tầm 10 câu mỗi lần đăng nha, chứ dài ntnay ngại làm lắm~
Đúng 0
Bình luận (1)






















