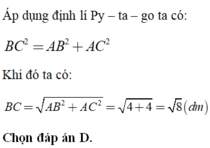Bài 1: (bạn tự vẽ hình vì hình cũng dễ)

Ta có: AB = AH + BH = 1 + 4 = 5 (cm)

Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)

Xét tam giác BCH vuông tại H có:

  \(HB^2+CH^2=BC^2\left(pytago\right)\)

  \(4^2+CH^2=5^2\)

  \(16+CH^2=25\)

\(\Rightarrow CH^2=25-16=9\)

\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)

Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé

Bài 2: Sử dụng pytago với tam giác ABH => AH

Sử dụng pytago với ACH => AC

\(\text{Xét}:\)\(\Delta CDE\)\(\text{và}\)\(\Delta CAB\)\(,\)\(\text{ta có:}\)

\(\widehat{C}\)\(:\)\(chung\)

\(\widehat{CDE}=\widehat{CAB}=90^o\)

\(\Rightarrow\Delta CDE\text{∽}\Delta CAB\left(g-g\right)\)

\(\Rightarrow\frac{CD}{DE}=\frac{CA}{AB}\)\(\text{hay}\)\(\frac{2}{DE}=\frac{4}{6}\)

\(\Rightarrow DE=\left(6.2\right):4=3\left(cm\right)\)

Trả lời:

Xét tam giác DEC và tam giác ABC có:

góc EDC = góc BAC = 90^o

góc C chung

=> tam giác DEC ~ tam giác ABC ( g - g )

=> DE/AB = CD/AC ( tỉ số đồng dạng )

=> DE/6 = 2/4

=> DE = 3 ( cm )

Vậy DE = 3 cm

C

C

C

tam giác ABC vc tại A (gt) => AB = AC = 4

vì tg ABC vuông nên : AB^2 + AC^2 = BC^2

=> BC^2 = 32

=> BC = \(\sqrt{32}\) do BC > 0 

Làm theo cách lớp 8:

Từ A kẻ AH _|_ BC (H nằm trên BC)

Mà tam giác ABC cân tại A => AH đồng thời là trung tuyến => BH = HC = 1cm

Xét tam giác AHB vuông tại H

=> AH² = AB² - BH² = 4² - 1² = 15cm

=> \(AH=\sqrt{15}cm\)

ΔAHC ~ ΔBDC (g.g) vì:

+ Góc C chung

+ \(\widehat{AHC}=\widehat{BDC}=90^0\)

=> \(\frac{AH}{AC}=\frac{BD}{BC}\Rightarrow BD=\frac{AH.BC}{AC}=\frac{2\sqrt{15}}{4}=\frac{\sqrt{15}}{2}cm\)

Vậy \(BD=\frac{\sqrt{15}}{2}cm\)

Xét \(\Delta AHC\left(\widehat{AHC}=90^o\right)\) có:

\(AC^2=AH^2+HC^2\) (định lí pitago)

\(\Rightarrow AH^2=AC^2-HC^2\)

\(\Rightarrow AH=\sqrt{5^2-4^2}=3\left(cm\right)\)

Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\) (hệ thức lượng trong tam giác vuông)

\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{AH^2}-\dfrac{1}{AC^2}\)

\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}\)

\(\Rightarrow AB=3,75\left(cm\right)\)

Xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có:

\(BC^2=AB^2+AC^2\) (định lí pitago)

\(\Rightarrow BC=\sqrt{3,75^2+5^2}=6,25\left(cm\right)\)

\(AH=\sqrt{AC^2-HC^2}=3\left(cm\right)\)

\(HB=\dfrac{AH^2}{HC}=\dfrac{3^2}{4}=2.25\left(cm\right)\)

BC=HB+HC=4+2,25=6,25(cm)

\(AB=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=3^2+4^2=25\)

hay BC=5(cm)

Xét ΔABC có

AD là đường phân giác trong ứng với cạnh BC(gt)

nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất đường phân giác của tam giác)

hay \(\dfrac{BD}{3}=\dfrac{CD}{4}\)

mà BD+CD=BC(D nằm giữa B và C)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{BC}{7}=\dfrac{5}{7}\)

Do đó: \(\dfrac{BD}{3}=\dfrac{5}{7}\)

hay \(BD=\dfrac{15}{7}cm\)

Vậy: \(BD=\dfrac{15}{7}cm\)