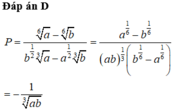a,a6 + 5,b3 + 21,8c ....... a,bc + 36,9

Những câu hỏi liên quan
1a,6+5,b3+21,8c a,bc+36,9
dien dau <,>,= (co loi giai thich)
Điền vào chỗ chấm dấu > , < hoặc = và nêu cách giải:
1a,6 + 6,b3 + 21,8c ........ a,bc + 36,9
1a,6 + 6,b3 + 21,8c ... a,bc+36,9
10,6+a+6,03+0,3+21,80+0,0c ... a+0,8+0,0c+36,9
38,43 +a,bc > a,bc+36,9
Đúng 0
Bình luận (0)
Rút gọn biểu thức
P
a
6
−
b
6
a
3
.
b
1
2
−
b
3
.
a...
Đọc tiếp
Rút gọn biểu thức P = a 6 − b 6 a 3 . b 1 2 − b 3 . a 1 2 , (với a , b > 0 )
A. ab 3
B. 1 ab
C. 1 ab 3
D. − 1 ab 3
cho a,b là 2 số thực phân biệt thỏa mãn a2-3a=b2-3b=1. Tính giá trị của:
a+b ; a2+b2 ; a3+b3 ; a4+b4 ; a5+b5 ; a6+b6
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AB a, BC a, CD
a
6
, SA
a
6
. Khi SA ⊥ (ABCD) thì khoảng cách từ giữa AD và SC là? A.
a
5
3
B.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B có AB = a, BC = a, CD = a 6 , SA = a 6 . Khi SA ⊥ (ABCD) thì khoảng cách từ giữa AD và SC là?

A. a 5 3
B. a 5 2
C. a 6 3
D. a 6 2
Đáp án C
Hướng dẫn giải: Do AD // BC
![]()
Kẻ AH ⊥ SB
Ta có B C ⊥ A B B C ⊥ S A
![]()
Mà A H ⊥ S B ⇒ A H ⊥ ( S B C )
⇒ A H ⊥ d ( A , ( S B C ) ) ta có:
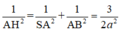
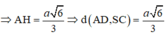
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
1, a6 + b3
2, x2 – 10x + 25
3, 8x3 – \(\dfrac{1}{8}\)
4, x2 + 4xy + 4y2
1, \(a^6+b^3=\left(a^2+b\right)\left(a^4-a^2b+b^2\right)\)
2, \(x^2-10x+25=\left(x-5\right)^2\)
3, \(8x^3-\dfrac{1}{8}=\left(2x-\dfrac{1}{2}\right)\left(4x^2+x+\dfrac{1}{4}\right)\)
4, \(x^2+4xy+4y^2=\left(x+2y\right)^2\)
Đúng 1
Bình luận (0)
1) \(a^6+b^3=\left(a^2\right)^3+b^3=\left(a^2+b\right)\left(a^4-a^2b+b^2\right)\)
2) \(x^2-10x+25=\left(x-5\right)^2\)
3) \(8x^3-\dfrac{1}{8}=\left(2x\right)^3-\left(\dfrac{1}{3}\right)^3=\left(2x-\dfrac{1}{3}\right)\left(4x^2+\dfrac{2x}{3}+\dfrac{1}{4}\right)\)
4) \(x^2+4xy+4y^2=\left(x+2y\right)^2\)
Đúng 0
Bình luận (1)
1: \(a^6+b^3=\left(a^2+b\right)\left(a^4-a^2b+b^2\right)\)
2: \(x^2-10x+25=\left(x-5\right)^2\)
3: \(8x^3-\dfrac{1}{8}=\left(2x-\dfrac{1}{2}\right)\left(4x^2+x+\dfrac{1}{4}\right)\)
4: \(x^2+4xy+4y^2=\left(x+2y\right)^2\)
Đúng 0
Bình luận (0)
2. Chứng minh rằng:
a. a3+ b3 = (a + b)3 - 3ab (a + b)
b. a3+ b3 + c3 - 3abc = (a + b + c) (a2 + b2 c2 - ab - bc - ca)
a )
`VP= (a+b)^3-3ab(a+b)`
`=a^3+3a^2b+3ab^2+b^3-3a^2b-3ab^2`
`=a^3+b^3 =VT (đpcm)`
b)
b) Ta có
`VT=a3+b3+c3−3abc`
`=(a+b)3−3ab(a+b)+c3−3abc`
`=[(a+b)3+c3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)2+c2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a2+b2+2ab+c2−ac−bc−3ab)`
`=(a+b+c)(a2+b2+c2−ab−bc−ca)=VP`
Đúng 0
Bình luận (0)
a) Ta có:
`VP= (a+b)^3-3ab(a+b)`
`=a^3 + b^3+3ab ( a + b )- 3ab ( a + b )`
`=a^3 + b^3=VT(dpcm)`
b) Ta có
`VT=a^3+b^3+c^3−3abc`
`=(a+b)^3−3ab(a+b)+c^3−3abc`
`=[(a+b)^3+c^3]−3ab(a+b+c)`
`=(a+b+c)[(a+b)^2+c^2−c(a+b)]−3ab(a+b+c)`
`=(a+b+c)(a^2+b^2+2ab+c^2−ac−bc−3ab)`
`=(a+b+c)(a^2+b^2+c^2−ab−bc−ca)=VP`
Đúng 0
Bình luận (0)
a+bc+b+ca+c+ab−a3+b3+c3abc2a+bc+b+ca+c+ab−a3+b3+c3abc2Tính giá trị biểu thức : A [ (a+b)2019 - c2019 ] [ (b+c)2019 - a2019 ] [ (a+c)2019 - b2019 ]
Đọc tiếp
Cho tam giác ABC cân tại A có AB=5, BC=8. Độ dài của vecto CA+BA bằng
A6. B8. C3. D10
Chọn D.10 bạn nhé, bn vẽ hbh ra và ad quy tắc hbh là OK
Đúng 0
Bình luận (6)