xin nhờ các cao nhân giải bài này giúp e với ạ. e thành tâm cảm ơn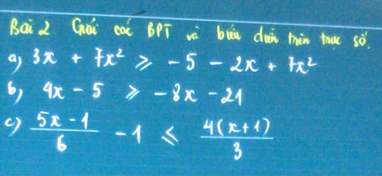

Những câu hỏi liên quan
xin các vị giúp e bài này với ạ, e cảm ơn rất nhiều
các vị giúp e bài này với ạ. e xin hậu tạ và cảm ơn

Câu 1.
a.Áp dụng tính chất đường phân giác, ta có:
\(\dfrac{AB}{AH}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{6}{8}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{CH}{8}=\dfrac{BC}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{CH+BC}{8+6}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(CH=\dfrac{5}{7}.8=\dfrac{40}{7}\)
\(BC=\dfrac{5}{7}.6=\dfrac{30}{7}\)
b.\(\Delta ABH\) là tam giác vuông vì:
\(HB^2=AB^2+AH^2\)
\(\Leftrightarrow10^2=6^2+8^2\) ( pitago đảo )
Áp dụng định lý pitago vào tam giác vuông ACB
\(AB^2=BC^2+AC^2\)
\(\Rightarrow AC=\sqrt{6^2-\dfrac{30}{7}^2}=\dfrac{12\sqrt{6}}{7}\)
\(S_{ABC}=\dfrac{1}{2}.BC.AC=\dfrac{1}{2}.\dfrac{30}{7}.\dfrac{12\sqrt{6}}{7}\simeq8,998cm^2\)
\(S_{ACH}=\dfrac{1}{2}.HC.AC=\dfrac{1}{2}.\dfrac{40}{7}.\dfrac{12\sqrt{6}}{7}\simeq11,997cm^2\)
Đúng 2
Bình luận (0)
các vị giúp e bài này với ạ. e xin hậu tạ và cảm ơn
Xét ΔABC có BD là phân giác
nên AB/AD=BC/CD
=>AB/4=BC/5
Đặt AB/4=BC/5=k
=>AB=4k; BC=5k
Theo đề, ta có: \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow9k^2=81\)
=>k=3
=>AB=12; BC=15
Đúng 1
Bình luận (0)
Vì BD là phân giác của \(\widehat{ABC}\) nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\Leftrightarrow\dfrac{4}{AB}=\dfrac{5}{BC}\Leftrightarrow BC=\dfrac{5AB}{4}\)
Có : AC=AD+DC=4+5=9cm
Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) ( định lí Pi-ta-go)
\(AB^2+81=\dfrac{25AB^2}{16}\)
\(81=\dfrac{25AB^2}{16}-\dfrac{16AB^2}{16}\)
\(\Leftrightarrow\dfrac{9AB^2}{16}=81\)
\(9AB^2=1296\)
\(AB^2=144\)
AB=12 cm
Có : \(BC=\dfrac{5AB}{4}=\dfrac{5.12}{4}=15cm\)
Đúng 1
Bình luận (0)
các vị giúp e bài này với ạ. e xin hậu tạ và cảm ơn
a:Xét ΔAMN có MB là tia phân giác
nên AB/BN=AM/MN=AN/MN(1)
Xét ΔAMN có NC là tia phân giác
nên AC/CM=AN/MN(2)
Từ (1) và (2) suy ra AB/BN=AC/CM
hay BC//MN
b: Xét ΔCBM có \(\widehat{CBM}=\widehat{CMB}\)
nên ΔCBM cân tại C
=>CB=CM=6cm
Xét ΔABC có BC//MN
nên BC/MN=AC/AM
\(\Leftrightarrow\dfrac{AC}{AC+6}=\dfrac{1}{2}\)
=>AC=6(cm)
=>AM=12(cm)
Đúng 1
Bình luận (0)
Xin nhờ mọi người giải giúp em 2 bài này với ạ. Em cảm ơn thật nhiều.
Đọc tiếp
Xin nhờ mọi người giải giúp em 2 bài này với ạ. Em cảm ơn thật nhiều.
\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
Đúng 4
Bình luận (0)
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)
Đúng 1
Bình luận (0)
Mn giúp e bài này với ạ:(( thầy giáo cho btvn mà e ko biết làm ntn😢 nhờ mn giúp e với ạ. E cảm ơn🥰🥰
Giúp e các bước giải của bài này với ạ, e gấp lắm.E cảm ơn ạ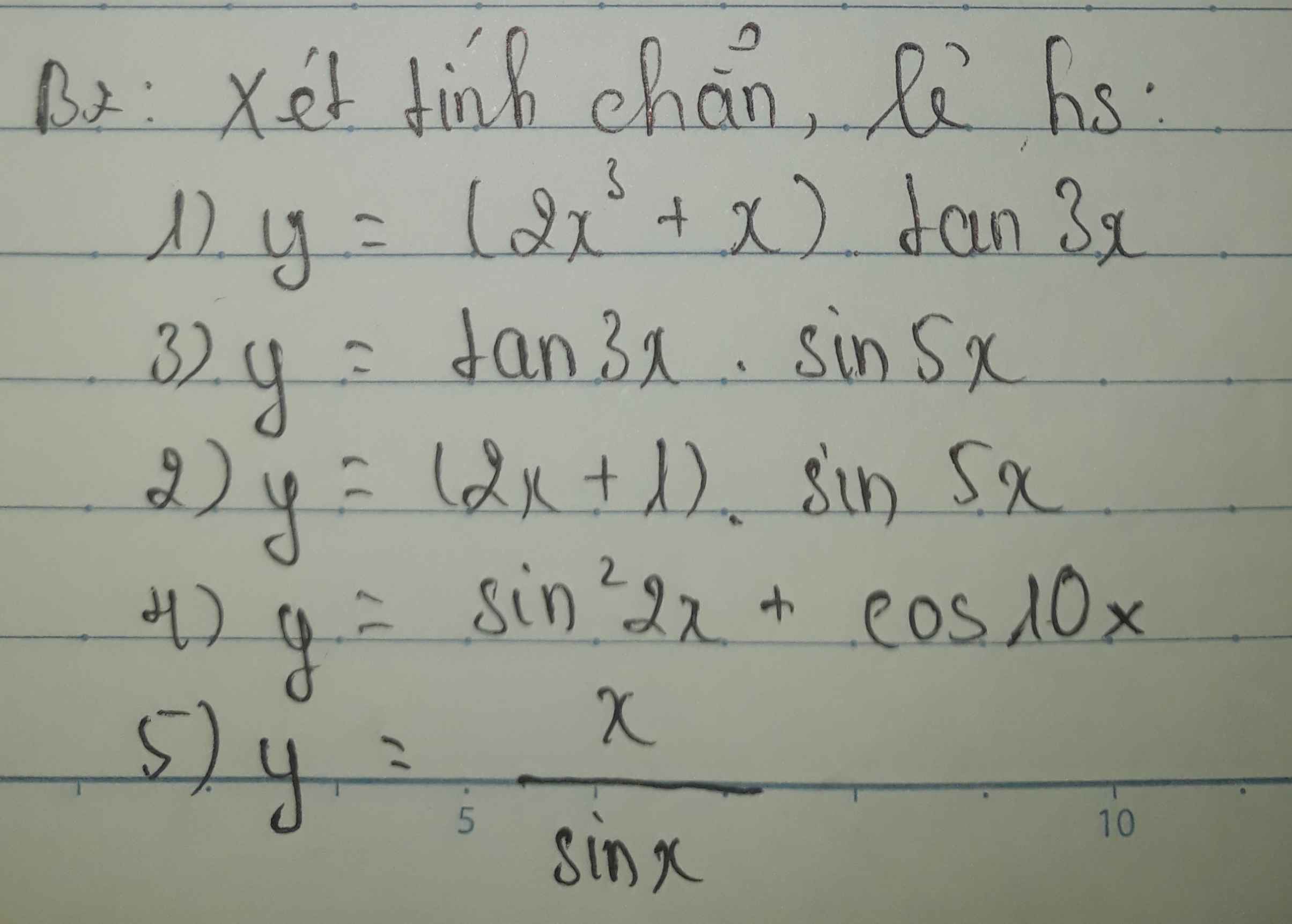
1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn
Đúng 1
Bình luận (0)
Cao nhân nào làm giúp e câu d với ạ? E đang cần gấp ạ, xin cảm ơn 
Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8
Đúng 1
Bình luận (0)
giúp e vài bài này với ạ, e xin cảm ơn và báo đáp
\(c2:3x+5x^2\ge-6+5x+5x^2\Leftrightarrow2x-6\le0\Leftrightarrow x\le3\)
\(c3:-x+7=6a-1\Leftrightarrow x=-\left(6a-1-7\right)=8-6a>0\Leftrightarrow a< \dfrac{4}{3}\)
\(c4:pt\Leftrightarrow\left(2019-x\right)^3+\left(2021-x\right)^3+\left[2x-4040\right]^3=0\left(1\right)\)
\(đặt:\left[\left(2019-x\right);\left(2021-x\right)\right]=\left\{u;v\right\}\)
\(\Rightarrow2x-4040=x-2019+x-2021=-u-v\)
\(\left(1\right)\Leftrightarrow u^3+v^3+\left(-u-v\right)^3=0\Leftrightarrow-3uv\left(u+v\right)=0\Leftrightarrow\left[{}\begin{matrix}u.v=0\\u=-v\end{matrix}\right.\)
\(u.v=0\Leftrightarrow\left[{}\begin{matrix}u=0\Leftrightarrow2019-x=0\Leftrightarrow x=2019\\v=0\Leftrightarrow2021-x=0\Leftrightarrow x=2021\end{matrix}\right.\)
\(u=-v\Leftrightarrow2019-x=x-2021\Leftrightarrow x=2020\)
\(\Rightarrow S=\left\{2019;2020;2021\right\}\)
Đúng 1
Bình luận (0)
Câu 2 :
\(\Leftrightarrow3x+5x^2+6-5x-5x^2\ge0\Leftrightarrow-2x+6\ge0\Leftrightarrow x\le3\)
Câu 4 :
PT <=> \(2019-x+2021-x+2x-4040=0\Leftrightarrow2019+2021-4040=0\)
( đúng )
Vậy pt có vô số nghiệm
Đúng 1
Bình luận (0)
















