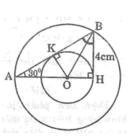
tam giác AHB có góc H =90∘, góc A=30∘,BH = 4cm. phân giác góc B cắt AH tại O. Vẽ (O; OH) và (O; OA). a) Chứng minh : (O; OH) tiếp xúc với cạnh AB. b) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.
Những câu hỏi liên quan
Cho tam giác AHB có góc H = 90 ° ,góc A = 30° và BH =4cm.Tia phân giác góc B cắt AH tại O. Vẽ đường tròn (O;OH) và đường tròn (O;OA). Chứng minh đường tròn (O;OH) tiếp xúc với cạnh AB
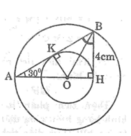Kẻ OK ⊥ AB (1)
Theo giả thiết ,OB là đường phân giác của góc B nên ta có:
OK = OH (tính chất đường phân giác) (2)
Từ (1) và (2) suy ra (O;OH) tiếp xúc với AB tại K
Đúng 0
Bình luận (0)
Cho tam giác AHB có góc H = 90 ° ,góc A = 30° và BH =4cm.Tia phân giác góc B cắt AH tại O. Vẽ đường tròn (O;OH) và đường tròn (O;OA). Tính diện tích hình vành khăn nằm giữa hai đường tròn trên
Cho tam giác AHB có \(\widehat{H}=90^0,\widehat{A}=30^0,BH=4cm\). Tia phân giác của góc B cắt AH tại O. Vẽ đường tròn (O; OH) và đường tròn (O; OA)
a) Chứng minh đường tròn (O; OH) tiếp xúc với cạnh AB
b) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên
Cho tam giác ABC cân tại A ( góc A < 90 độ ). Vẽ BH vuông góc vs AC tại H, CK vuông góc với AH tại K. C/M :
a) tam giác AHB=tam giác AKC
b) BH cắt CK ở M. Chứng minh AM là tia phân giác của góc BAC
c) AM vuông góc BC
Xem thêm câu trả lời
Cho tam giác ABC có AB=AC=10cm, BC=12cm. Vẽ AH vuông góc BC tại H a) Chứng minh tam giác AHB=tam giác AHC, từ đó chứng minh AH là tia phân giác của góc A b) Tính độ dài AH c) Từ B kẻ Bx vuông góc AB, từ C kẻ Cy vuông góc AC, chúng cắt nhau tại O. Tam giác ABC là tam giác gì, vì sao?
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>góc BAH=góc CAH
=>AH là phân giác của góc BAC
b: BH=CH=12/2=6cm
AH=căn 10^2-6^2=8cm
Đúng 0
Bình luận (0)
a) Cho tam giác ABC có góc A=90o và góc B lớn hơn góc C,vẽ AH vuông góc với BC tại H. Tia phân giác của góc HAC cắt BC tại D. Chứng minh góc BDA= góc BAD.
b) Tia phân giác của góc BAC cắt BC tại E, cho biết góc AEC - góc AEB=30o. Tính số đo góc ABC và góc CAD.
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, có 𝐵𝐴𝐶 = 700 . Vẽ AH vuông góc với BC. a) Chứng minh tam giác AHB = tam giác AHC và AH là tia phân giác của góc BAC. b) So sánh độ dài cạnh AH và BH. c) Từ H vẽ HD vuông góc AB và HE vuông góc AC . Tam giác ADE là tam giác gì ? Vì sao? d) Qua D vẽ đường thẳng DK vuông góc với BC tại K. Chứng minh DK < KE
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
b: \(\widehat{BAC}=70^0\)
nên \(\widehat{BAH}=35^0\)
=>\(\widehat{B}=55^0\)
=>BH<AH
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE
hay ΔADE cân tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AH phân giác góc A cắt BC tại H . chứng minh
a. Tam giác AHB = tam giác AHC
b. BH = Hc
giúp em với ạ
a.Ta có : tam giác ABC cân tại A
=>AB=AC;B=C
Xét tam giác AHB và tam giác AHC ta có:
B=C(gt)
AB=AC(gt)
BAH=HAC( p/g)
=>tam giác AHB=tam giác AHC(g-c-g)(dpcm)
b.Theo câu a ta có:
BH=HC (2 cạnh tương ứng)(dpcm)
Đúng 3
Bình luận (0)
Cho tam giác ABC có góc A = 90 độ, vẽ AH vuông góc với BC (CH thuộc BC). Vẽ các tia phân giác của góc B và góc HAC. Chúng cắt nhau tại O. Chứng minh góc AOB= 90 độ.
TAm giác ABC vuông tại A => ABC + C = 90 độ (1)
TAm giác AHC vuông tại H => HAC + C = 90độ (2)
Từ (1) và (2) => ABC = HAC (3)
Ta có OBA = 1/2 ABC ( BO là phâ n giác ) (4)
Từ (3) và (4) => OBA = 1/2 HAC
OAH = 1/2 HAC ( AO là phân giác)
=>ABO + OAB = 1/2 . HAC + OAH + HAB = 1/2 .HAC + 1/2 .HAC + HAB = HAC + HAB = BAC = 90 độ ( TAm giác ABC vuông tại A )
TAm giác OAB có OBA + OAB = 90 độ => AOB = 90 độ
=> ĐPCM
Đúng 0
Bình luận (0)
Gọi BO giao với AH tại K
Tam giác ABC vuông tại A
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)(1)
Tam giác AHC có \(\widehat{H}=90^o\)
\(\Rightarrow\widehat{HAC}+\widehat{C}=90^o\)(2)
Từ (1) và (2) => \(\widehat{B}=\widehat{HAC}\)
\(\Rightarrow\widehat{HBO}=\widehat{HAO}\)
lại có \(\hept{\begin{cases}\widehat{HBO}+\widehat{BKH}=90^o\\\widehat{HAO}+\widehat{AKO}=\widehat{HBO}+\widehat{BKH}\end{cases}}\)( vì góc BKH và góc AKO bằng nhau 2 góc đối đỉnh )
\(\Rightarrow\widehat{HAO}+\widehat{AKO}=90^o\)
\(\Rightarrow\widehat{AOB}=90^o\)