Các câu hỏi tương tự
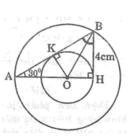
tam giác AHB có góc H =90∘, góc A=30∘,BH = 4cm. phân giác góc B cắt AH tại O. Vẽ (O; OH) và (O; OA). a) Chứng minh : (O; OH) tiếp xúc với cạnh AB. b) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên.
Cho tam giác AHB có góc H = 90 ° ,góc A = 30° và BH =4cm.Tia phân giác góc B cắt AH tại O. Vẽ đường tròn (O;OH) và đường tròn (O;OA). Chứng minh đường tròn (O;OH) tiếp xúc với cạnh AB
Cho đường tròn (O) có bán kính OA = 5cm. Trên OA lấy điểm H sao cho OH = 3cm. Qua điểm H vẽ đường thẳng vuông góc với OA, cắt đường tròn tại hai điểm B và C. Tiếp tuyến của đường tròn (O) tại B cắt đường thẳng OA tại M.
a) Chứng minh tam giác OBM vuông
b) Tính BH,BM
c) Chứng minh MC là tiếp tuyến
d) Tìm tâm của đường tròn đi qua bốn điểm O, B, M, C.
Cho đường tròn (O) có bán kính OA = 5cm. Trên OA lấy điểm H sao cho OH = 3cm. Qua điểm H vẽ đường thẳng vuông góc với OA, cắt đường tròn tại hai điểm B và C. Tiếp tuyến của đường tròn (O) tại B cắt đường thẳng OA tại M.
a) Chứng minh tam giác OBM vuông
b) Tính BH,BM
c) Chứng minh MC là tiếp tuyến
d) Tìm tâm của đường tròn đi qua bốn điểm O, B, M, C.
Cho tam giác ABC có góc A 90; C30 và AB 3cm. Tia phân giác của góc B cắt AC tại O. Kẻ OK vuông góc với BC cắt BC tại K.a. Vẽ hìnhb. chứng minh tứ giác ABKO nội tiếp đường trònc. chứng minh BC là tiếp tuyến của đường tròn tâm O bán kính OAd. tính diện tích tứ giác OABKe. tứ C kẻ tiếp tuyến CL với đường tròn tâm O bán kính OA ( L là tiếp điểm khác K). Chứng minh ba điểm B, O, L thẳng hàng
Đọc tiếp
Cho tam giác ABC có góc A = 90; C=30 và AB =3cm. Tia phân giác của góc B cắt AC tại O. Kẻ OK vuông góc với BC cắt BC tại K.
a. Vẽ hình
b. chứng minh tứ giác ABKO nội tiếp đường tròn
c. chứng minh BC là tiếp tuyến của đường tròn tâm O bán kính OA
d. tính diện tích tứ giác OABK
e. tứ C kẻ tiếp tuyến CL với đường tròn tâm O bán kính OA ( L là tiếp điểm khác K). Chứng minh ba điểm B, O, L thẳng hàng
Cho đường tròn (O; 4cm) có đường kính BC. Gọi A là điểm nằm trên đường tròn sao cho góc vuông ABC30°. Trên tia AC lấy điểm P sao cho APAB. Đường thẳng vuông góc hạ từ P xuống BC cắt BC ở H và cắt BA ở D. Kẻ PB cắt đường tròn (O) tại I.a)Tính độ dài đường tròn và diện tích hình tròn.b)Chứng minh tứ giác ACHD nội tiếp.c)Tam giác ABP là tam giác gì? Tính góc vuông APB, sđ cung ACI.d)Tính độ dài cung tròn cung ACI và diện diện của hình quạt OAI.
Đọc tiếp
Cho đường tròn (O; 4cm) có đường kính BC. Gọi A là điểm nằm trên đường tròn sao cho góc vuông ABC=30°. Trên tia AC lấy điểm P sao cho AP=AB. Đường thẳng vuông góc hạ từ P xuống BC cắt BC ở H và cắt BA ở D. Kẻ PB cắt đường tròn (O) tại I.
a)Tính độ dài đường tròn và diện tích hình tròn.
b)Chứng minh tứ giác ACHD nội tiếp.
c)Tam giác ABP là tam giác gì? Tính góc vuông APB, sđ cung ACI.
d)Tính độ dài cung tròn cung ACI và diện diện của hình quạt OAI.
Cho tam giác ABC vuông tại A có ABAC, đường ca AH. Vẽ tròn đường kính BH cắt AB tại E, đường tròn đường kính HC cắt AC tại F.a) Chứng minh tứ giác AEHF nội tiếp đường tròn ? Tìm tâm và đường kính của đường tròn ngoại tiếp tứ giác AEHFb) Cứng minh AE.AB AF.ACc) Chứng minh bốn điểm B, E, F, C cùng nằm trên một đường trònd) Biết góc ABC bằng 30o, BH 4cm. tính tổng diện tích hình viên phân giới hạn bởi dây BE; dây HE và cung HE
Đọc tiếp
Cho tam giác ABC vuông tại A có AB>AC, đường ca AH. Vẽ tròn đường kính BH cắt AB tại E, đường tròn đường kính HC cắt AC tại F.
a) Chứng minh tứ giác AEHF nội tiếp đường tròn ? Tìm tâm và đường kính của đường tròn ngoại tiếp tứ giác AEHF
b) Cứng minh AE.AB = AF.AC
c) Chứng minh bốn điểm B, E, F, C cùng nằm trên một đường tròn
d) Biết góc ABC bằng 30o, BH =4cm. tính tổng diện tích hình viên phân giới hạn bởi dây BE; dây HE và cung HE
B1: Cho tam giác ABC vuông tại A, biết AB 6cm, AC 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.a) Chứng minh tứ giác AEHF là hình chữ nhậtb) Chứng minh tứ giác BEFC nội tiếpc) Gọi I là trung điểm của BC.Chứng minh AI vuông góc với EFd) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEFC.Tính diện tích hình tròn tâm K.B2: Cho ABC nhọn, đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và D, CE cắt BD tại Ha) Chứng minh tứ giác ADHE nội tiếpb) AH cắ...
Đọc tiếp
B1: Cho tam giác ABC vuông tại A, biết AB = 6cm, AC = 8cm. Vẽ đường cao AH, đường tròn tâm O đường kính AH cắt AB tại E và cắt AC tại điểm F.
a) Chứng minh tứ giác AEHF là hình chữ nhật
b) Chứng minh tứ giác BEFC nội tiếp
c) Gọi I là trung điểm của B
C.Chứng minh AI vuông góc với EF
d) Gọi K là tâm của đường tròn ngoại tiếp tứ giác BEF
C.Tính diện tích hình tròn tâm K.
B2: Cho ABC nhọn, đường tròn (O) đường kính BC cắt AB, AC lần lượt tại E và D, CE cắt BD tại H
a) Chứng minh tứ giác ADHE nội tiếp
b) AH cắt BC tại F. chứng minh FA là tia phân giác của góc DFE
c) EF cắt đường tròn tại K ( K khác E). chứng minh DK// AF
d) Cho biết góc BCD = 450 , BC = 4 cm. Tính diện tích tam giác ABC
B 3: cho đường tròn ( O) và điểm A ở ngoài (O)sao cho OA = 3R. vẽ các tiếp tuyến AB, AC với đường tròn (O) ( B và C là hai tiếp tuyến )
a) Chứng minh tứ giác OBAC nội tiếp
b) Qua B kẻ đường thẳng song song với AC cắt ( O) tại D ( khác B). đường thẳng AD cắt ( O) tại E. chứng minh AB2= AE. AD
c) Chứng minh tia đối của tia EC là tia phân giác của góc BEA
d) Tính diện tích tam giác BDC theo R
B4: Cho tam giác ABC nhọn, AB >AC, nội tiếp (O,R), hai đường cao AH, CF cắt nhau tại H
a) Chứng minh tứ giác BDHF nội tiếp? Xác định tâm của đường tròn ngoại tiếp tứ giác đó
b) Tia BH cắt AC tại E. chứng minh HE.HB= HF.HC
c) Vẽ đường kính AK của (O). chứng minh AK vuông góc với EF
d) Trường hợp góc KBC= 450, BC = R. tính diện tích tam giác AHK theo R
B5: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Ba đương cao AE, BF, CK cắt nhau tại H. Tia AE, BF cắt đường tròn tâm O lần lượt tại I và J.
a) Chứng minh tứ giác AKHF nội tiếp đường tròn.
b) Chứng minh hai cung CI và CJ bằng nhau.
c) Chứng minh hai tam giác AFK và ABC đồng dạng với nhau
B6: Cho tam giác ABC nhọn nội tiếp đường tròn ( O; R ),các đường cao BE, CF .
a)Chứng minh tứ giác BFEC nội tiếp.
b)Chứng minh OA vuông góc với EF.
1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB HA). Vẽ dây CD vuông góc với AB tại H. CMR:a) Góc BCA 90 độ b) CH . HD HB . HA c) Biết OH R/2. Tính diện tích tam giác ACD theo...
Đọc tiếp
1/ Cho đường tròn (O) đường kính AB và 1 điểm C trên đường tròn.Từ O kẻ 1 đường thảng song song với dây AC , đường thảng này cắt tiếp tuyến tại B của đường tròn ở điển C A) CM: OD là phân giác của góc BOC b) CN: CD là tiếp tuyến của đường tròn
2/ Cho đường tròn (O;R), H là điểm bên trong đường tròn (H không trùng với O). Vẽ đưởng kính AB đi qua H (HB < HA). Vẽ dây CD vuông góc với AB tại H. CMR:
a) Góc BCA = 90 độ b) CH . HD = HB . HA c) Biết OH = R/2. Tính diện tích tam giác ACD theo R
3/ Cho tam giác MAB, vẽ đường tròn (O) đường kính AB cắt MA ở C, cắt MB ở D. Kẻ AP vuông góc CD , BQ cuông góc CD. Gọi H là giao điểm AD và BC. CM:
a) CP = DQ b) PD . DQ = PA . BQ và QC . CP = PD . QD c) MH vuông góc AB\
4/ Cho đường tròn (O;5cm) đường kính AB, gọi E là 1 điểm trên AB sao cho BE = 2cm.Qua trung điểm kH của đoạn AE vẽ dây cung CD vuông góc AB.
a) Tứ giác ACED là hình gì? Vì sao? b)Gọi I là giao điểm của DE với BC. CMR:I thuộc đường tròn (O') đường kính EB
c) CM HI là tiếp điểm của đường tròn (O') d) Tính độ dài đoạn HI
5/ Cho đường tròn (0) đường kính AB = 2R. Gọi I là trung điểm của AO, qua I kẻ dây CD vuông góc với OA.
a) Tứ giác ACOD là hình gì? tại sao?
b) CM tam giác BCD đều
c) Tính chu vi và diện tích tam giác BCD theo R
6/ Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 9cm; BC = 15cm
a) Tính độ dài các cạnh AC, AH, BH, HC
b) Vẽ đường tròn tâm B, bán kính BA. Tia AH cắt (B) tại D. CM: CD là tiếp tuyến của (B;BA)
c) Vẽ đường kính DE. CM: EA // BC
d) Qua E vẽ tiếp tuyến d với (B). Tia CA cắt d tại F, EA cắt BF tại G. CM: CF = CD + EF và tứ giác AHBG là hình chữ nhật
7/ Cho đường tròn (O) đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. gọi E là giao điểm của AC và BM.
a) CMR: NE vuông góc AB
b) Gọi F là điểm đối xứng với E qua M. CMR: FA là tiếp tuyến của đường tròn (O)
c) CM: FN là tiếp tuyến của đường tròn (B;BA)
8/ Cho nửa đường tròn (O), đường kính AB.Từ một điểm M trên nửa đường tròn ta vẽ tiếp tuyến xy. Từ A ta vẽ AD vuông góc với xy tại D
a) CM: AD // OM
b) Kẻ BC vuông góc với xy tại C. CMR: MC = MD