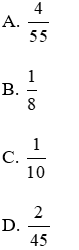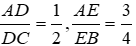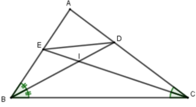
Ta có: A D A B = D C B C  (t/c)

⇒ A D 4 = D C 6 = A D + D C 4 + 6 = 5 10 = 1 2

=> AD = 4. 1 2 = 2, DC = 6. 1 2  = 3

Suy ra:

D I I B = D C C B = 3 6 = 1 2 ⇒ D I D B = 1 3 B E E A = B C A C = 6 5 ⇒ B E B A = 6 11 A D D C = 2 3 ⇒ A D A C = 2 5

Suy ra S D I E = 1 3 S B D E

⇒ S D I E = 1 3 . 6 11 . 2 5 = 4 55 S A B C

Vậy  S D I E S A B C = 4 55

Đáp án: A

cj tham khảo bài này nha!

a, Theo tính chất đường phân giác ta có : \(\frac{AD}{AB}=\frac{DC}{BC}\)=> \(\frac{AD}{4}=\frac{DC}{6}\)=> \(\frac{AD}{2}=\frac{DC}{3}=\frac{AD+DC}{2+3}=\frac{AC}{5}=\frac{5}{5}=1\)

=> \(\hept{\begin{cases}AD=2\\DC=3\end{cases}}\)

a) Áp  dụng tính chất đường phân giác ta có:

 \(\frac{AD}{CD}=\frac{AB}{BC}=\frac{4}{6}=\frac{2}{3}\)

\(\Leftrightarrow\frac{AD}{2}=\frac{AB}{3}=\frac{AD+AB}{2+3}=1\)

\(\Leftrightarrow AD=2;AB=3\)

mấy bạn giúp mik ý b đc ko

TK

Sửa đề: Các đường phân giác BD và CE cắt nhau ở I

a.Áp dụng t/c đường phân giác góc B, ta có:

\(\dfrac{AB}{BC}=\dfrac{AD}{CD}\)

\(\Leftrightarrow\dfrac{4}{6}=\dfrac{AD}{CD}\) \(\Leftrightarrow\dfrac{2}{3}=\dfrac{AD}{CD}\) \(\Leftrightarrow\dfrac{CD}{3}=\dfrac{AD}{2}\)

Áp dụng t/c dãy tỉ số bằng nhau, ta có:

\(\dfrac{CD}{3}=\dfrac{AD}{2}=\dfrac{CD+AD}{3+2}=\dfrac{AC}{5}=\dfrac{5}{5}=1\)

\(\Rightarrow CD=1.3=3cm\)

\(\Rightarrow AD=1.2=2cm\)

b.Áp dụng t/c đường phân giác góc C, ta có:

\(\dfrac{CA}{CB}=\dfrac{AE}{BE}\)

\(\Leftrightarrow\dfrac{5}{6}=\dfrac{AE}{BE}\)\(\Leftrightarrow\dfrac{BE}{6}=\dfrac{AE}{5}\)

Áp dụng t/c dãy tỉ số bằng nhau, ta có:

\(\dfrac{BE}{6}=\dfrac{AE}{5}=\dfrac{BE+AE}{6+5}=\dfrac{AB}{11}=\dfrac{4}{11}\)

\(\Rightarrow BE=\dfrac{4}{11}.6=\dfrac{24}{11}cm\)

\(\Rightarrow AE=\dfrac{4}{11}.5=\dfrac{20}{11}cm\)

H là điểm nào hả bạn?

TK
 

Vậy AB = 4cm, BC = 8cm, AC = 6cm

Đáp án cần chọn là: C

C

Gọi đường cao chung của 2 tam giác ABD và ACD là AH

Xét tam giác ABC có:

 AD là đường phân giác

=>\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)

=>\(\dfrac{DB}{DB+DC}=\dfrac{AB}{AB+AC}\)

=>\(\dfrac{DB}{BC}=\dfrac{6}{6+4}\)

=>\(\dfrac{DB}{5}=\dfrac{6}{10}\)

=>DB=3cm

CMTT:DC=2cm

Ta có:\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{\dfrac{1}{2}.AH.BD}{\dfrac{1}{2}.AH.DC}=\dfrac{BD}{DC}=\dfrac{3}{2}\)

-Xét △ABC có: AD là đường phân giác (gt).

\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{6}{4}=\dfrac{3}{2}\) (định lí đường phân giác).

\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{DB}{DC}=\dfrac{3}{2}\)

mik chịu

áp dụng tính chất đường phân giác ta có : AD/DC=AB/BC  hay AD/AB=DC/BC  

theo tính chất của dãy tỉ số bằng nhau, ta co: AD/AB=DC/BC =( AD+DC)/ (AB+BC)=6/10=3/5

VẬY AD = 3/5 x AB=3/5 x 6 =18/5 cm

dễ mà!!!!!!!