Viết phương trình tiếp tuyến (C): y=\(x^3-3x+2\) biết tiếp tuyến có hệ số vuông góc bằng 9

Những câu hỏi liên quan
Cho hàm số \(y=\dfrac{-1}{3x^2+x+2}\) có đồ thị (C). Viết phương trình tiếp tuyến biết:
a) Có hệ số góc bằng 1
b) Tiếp tuyến song song với Δ có phương trình \(y=-3x+2\)
c) Tiếp tuyến vuông góc với phương trình x+8y+1=0
Cho hàm số y = x 3 3 + 3 x - 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến có hệ số góc k= -9
A. y+16= -9(x+3)
B. y-16= -9(x-3)
C. y= -9(x+3)
D. y-16= -9(x+3)
Cho hàm số
(
C
)
:
y
x
3
-
3
x
+
2
.
Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến đó bằng 9 là: A.
y
9
x
-
4
h
o
ặ
c
y
9
x...
Đọc tiếp
Cho hàm số ( C ) : y = x 3 - 3 x + 2 . Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến đó bằng 9 là:
A. y = 9 x - 4 h o ặ c y = 9 x + 18
B. y = 9 x + 5 h o ặ c y = 9 x - 11
C. y = 9 x - 1 h o ặ c y = 9 x + 4
D. y = 9 x + 8 h o ặ c y = 9 x + 5
Chọn A
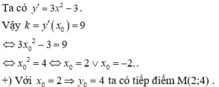
Phương trình tiếp tuyến tại M là
![]()
![]()
![]()
Phương trình tiếp tuyến tại N
![]()
Vậy có hai tiếp tuyến cần tìm là
![]()
Đúng 0
Bình luận (0)
Viết phương trình tiếp tuyến đường cong y = x 3 .
a. Tại điểm - 1 ; 1 ;
b. Tại điểm có hoành độ bằng 2;
c. Biết hệ số góc của tiếp tuyến bằng 3.
Với mọi x0 ∈ R ta có:
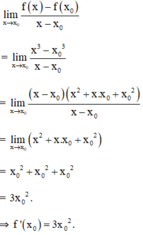
a) Tiếp tuyến của y = x3 tại điểm (-1; -1) là:
y = f’(-1)(x + 1) + y(1)
= 3.(-1)2(x + 1) – 1
= 3.(x + 1) – 1
= 3x + 2.
b) x0 = 2
⇒ y0 = f(2) = 23 = 8;
⇒ f’(x0) = f’(2) = 3.22 = 12.
Vậy phương trình tiếp tuyến của y = x3 tại điểm có hoành độ bằng 2 là :
y = 12(x – 2) + 8 = 12x – 16.
c) k = 3
⇔ f’(x0) = 3
⇔ 3x02 = 3
⇔ x02 = 1
⇔ x0 = ±1.
+ Với x0 = 1 ⇒ y0 = 13 = 1
⇒ Phương trình tiếp tuyến : y = 3.(x – 1) + 1 = 3x – 2.
+ Với x0 = -1 ⇒ y0 = (-1)3 = -1
⇒ Phương trình tiếp tuyến : y = 3.(x + 1) – 1 = 3x + 2.
Vậy có hai phương trình tiếp tuyến của đường cong y = x3 có hệ số góc bằng 3 là y = 3x – 2 và y = 3x + 2.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
3
+
3
x
2
-
2
có đồ thị là (C) Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc
k
-
9
A.
y
+
16
-
9
(
x
+
3
)...
Đọc tiếp
Cho hàm số y = x 3 3 + 3 x 2 - 2 có đồ thị là (C) Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc k = - 9
A. y + 16 = - 9 ( x + 3 )
B. y = - 9 ( x + 3 )
C. y - 16 = - 9 ( x - 3 )
D. y - 16 = - 9 ( x + 3 )
Cho hàm số
y
x
3
3
+
3
x
2
-
2
có đồ thị là (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc
k
-
9
A.
y
+
16
-
9
x
+...
Đọc tiếp
Cho hàm số y = x 3 3 + 3 x 2 - 2 có đồ thị là (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc k = - 9
A. y + 16 = - 9 x + 3
B. y = - 9 x + 3
C. y - 16 = - 9 x - 3
D. y - 16 = - 9 x + 3
Cho hàm số
y
x
3
3
+
3
x
2
-
2
có đồ thị là (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc k -9...
Đọc tiếp
Cho hàm số y = x 3 3 + 3 x 2 - 2 có đồ thị là (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc k= -9.
![]()
![]()
![]()
![]()
Cho hàm số \(y=x^3-3x+1\) (C). Viết pt tiếp tuyến của đồ thị (C) biết
a) Hệ số góc của tiếp tuyến bằng 9
b) Tiếp tuyến vuông góc với trục Oy
\(y'=3x^2-3\)
a. \(y'=9\Rightarrow3x^2-3=9\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow y=5\\x=-2\Rightarrow y=-1\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=9\left(x-2\right)+5\\y=9\left(x+2\right)-1\end{matrix}\right.\)
b. Tiếp tuyến vuông góc Oy nên nhận \(\left(0;1\right)\) là 1 vtpt \(\Rightarrow\) có hệ số góc \(k=0\)
\(\Rightarrow3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=-1\\x=-1\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-1\\y=3\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho hàm số y = x 3 + 3 x 2 + 1 có đồ thị là (C). Viết phương trình tiếp tuyến của (C): Biết rằng tiếp tuyến có hệ số góc là 9.












