Giúp mình với thanks 

Những câu hỏi liên quan
Giúp mình với thanks
Đọc tiếp
Giúp mình với thanks
a) \(\dfrac{x-1}{x+5}=\dfrac{6}{7}\left(đk:x\ne-5\right)\)
\(\Rightarrow7\left(x-1\right)=6\left(x+5\right)\)
\(\Rightarrow x=37\left(tm\right)\)
b) \(\dfrac{x^2}{6}=\dfrac{24}{49}\)
\(\Rightarrow x^2=\dfrac{24.6}{49}=\dfrac{144}{49}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{7}\\x=-\dfrac{12}{7}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
giúp mình với nhé, mình đang cần gấp!Thanks!
Đọc tiếp
giúp mình với nhé, mình đang cần gấp!
Thanks!
Giúp mình với ạ!!! Thanks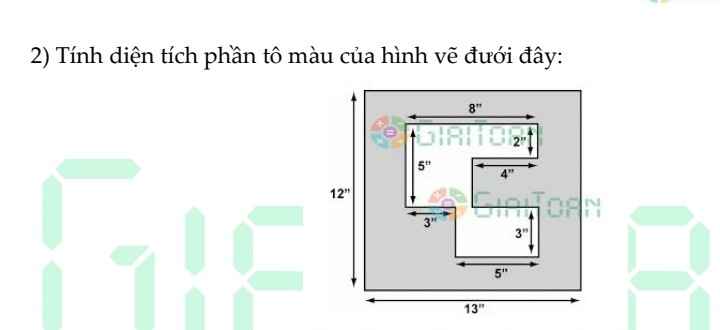

giúp mình với
thanks nhìu
a: \(2^{300}=8^{100}\)
\(3^{200}=9^{100}\)
mà 8<9
nên \(2^{300}< 3^{200}\)
Đúng 1
Bình luận (1)
Giúp mình với ạ!thanks!
Giúp mình với thanks ạ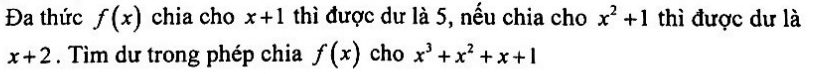
Giúp mình với ạ thanks!!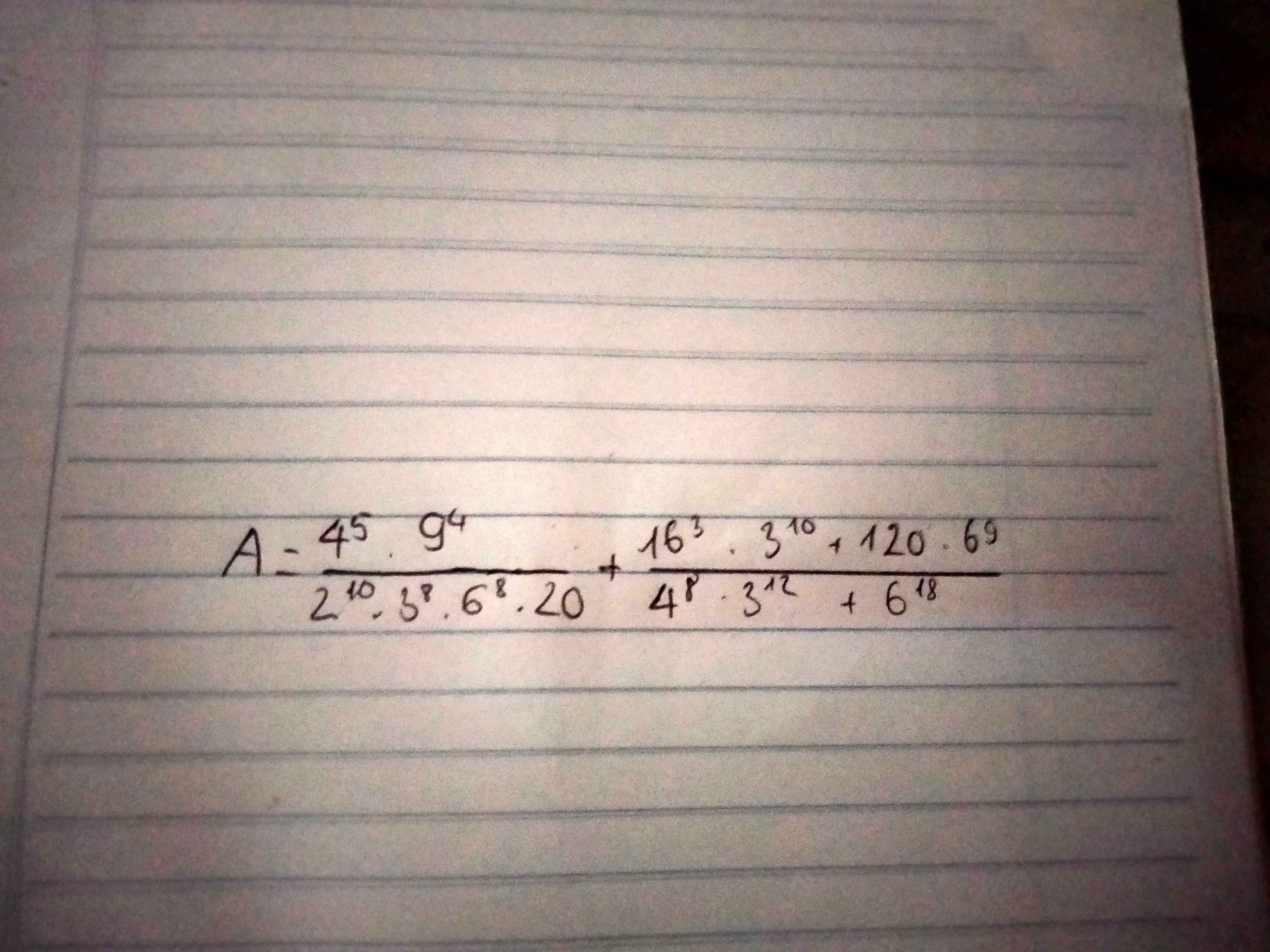
\(A=\dfrac{2^{10}\cdot3^8}{2^{10}\cdot3^8\cdot2^8\cdot3^8\cdot2^2\cdot5}+\dfrac{2^{12}\cdot3^{10}+2^3\cdot3\cdot5\cdot2^9\cdot3^9}{2^{16}\cdot3^{12}+2^{18}\cdot3^{18}}\\ A=\dfrac{1}{2^{10}\cdot3^8\cdot5}+\dfrac{2^{12}\cdot3^{10}\left(1+5\right)}{2^{16}\cdot3^{12}\left(1+2^2\cdot3^6\right)}\\ A=\dfrac{1}{2^{10}\cdot3^8\cdot5}+\dfrac{6}{2^4\cdot3^2\cdot2917}=\dfrac{1}{2^{10}\cdot3^8\cdot5}+\dfrac{1}{2^3\cdot3\cdot2917}\)
Đúng 1
Bình luận (0)
giúp mình với, nhanh ạ, mình đang cần gấp, thanks
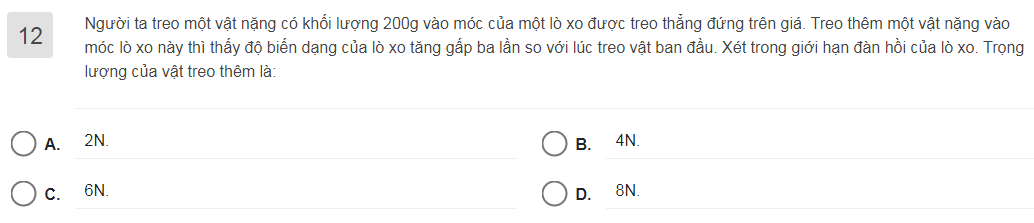
giúp mình bài này với mình cần gấp Thanks ạ
Bài 6:
a) \(x^2-2x+4=\left(x^2-2x+1\right)+3=\left(x-1\right)^2+3>0\forall x\)
b) \(-x^2+4x-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1< 0\forall x\)
c) \(\left(x-2\right)\left(x-4\right)+3=x^2-6x+11=\left(x^2-6x+9\right)+2=\left(x-3\right)^2+2>0\forall x\)
d) \(-2x^2+5x-19=\dfrac{-4x^2+10x-38}{2}=\dfrac{-\left(4x^2-10x+6,25\right)-31,75}{2}=\dfrac{-\left(2x-2,5\right)^2-31,75}{2}< 0\forall x\)
Đúng 2
Bình luận (1)
Câu 4:
a) \(x^5-x^3-x^2+1=\left(x^5-x^3\right)-\left(x^2-1\right)=x^3\left(x^2-1\right)-\left(x-1\right)\left(x+1\right)=x^3\left(x-1\right)\left(x+1\right)-\left(x-1\right)\left(x+1\right)=\left(x-1\right)\left(x+1\right)\left(x^3-1\right)=\left(x-1\right)^2\left(x+1\right)\left(x^2+x+1\right)\)
Đúng 0
Bình luận (0)
Câu 5:
\(a^3+b^3=3ab-1\\ \Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)-3ab+1=0\\ \Leftrightarrow\left(a+b+1\right)\left(a^2+2ab+b^2-a-b+1\right)-3ab\left(a+b+1\right)=0\\ \Leftrightarrow\left(a+b+1\right)\left(a^2+b^2+1-ab-a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a+b+1=0\left(vô.lí.do.a,b>0\right)\\a^2+b^2+1-ab-a-b=0\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow2a^2+2b^2+2-2ab-2a-2b=0\\ \Leftrightarrow\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}a-b=0\\a-1=0\\b-1=0\end{matrix}\right.\Leftrightarrow a=b=1\)
Vậy \(T=\left(1-2\right)^{2020}+\left(1-1\right)^{2021}=\left(-1\right)^{2020}+0=1\)
Đúng 2
Bình luận (1)

























