Giúp mik giải bài 4 vs câu d bài 2 zứi. :^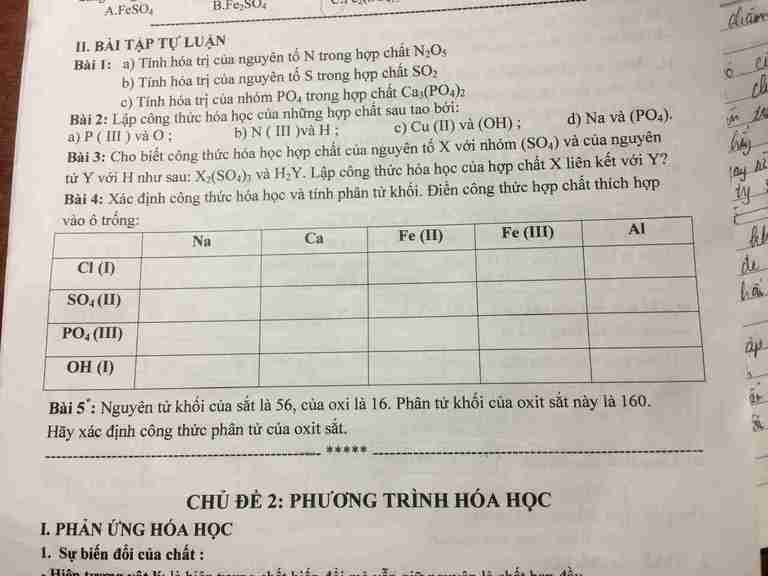

Những câu hỏi liên quan
Giúp mik câu d vs bài 4, mik cần gấp, mong ai đg thức giúp mik vs ạ
Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36
Đúng 0
Bình luận (1)
Giải giúp mik câu bài vs 
Ai giúp mik câu C và D bài 2 vs 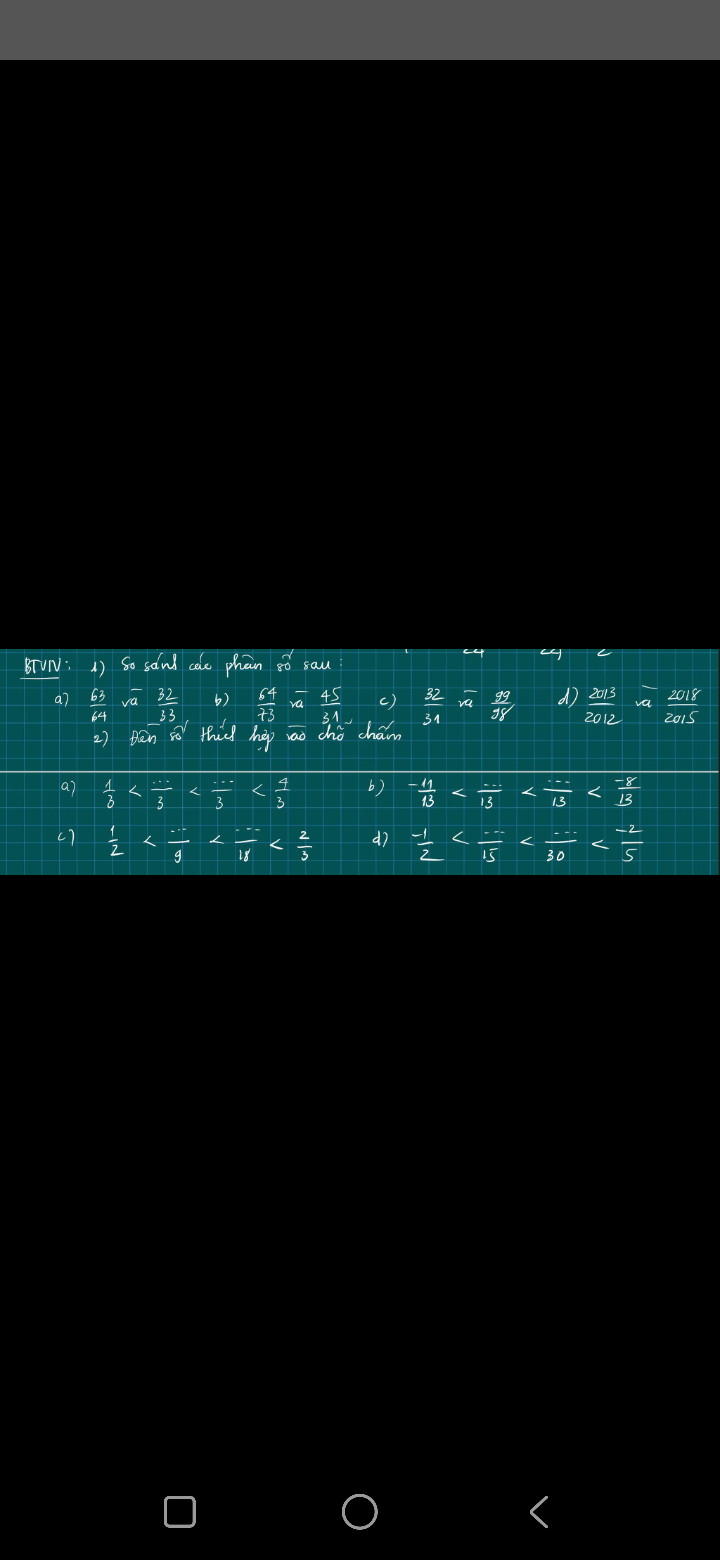
c: Gọi hai số cần tìm là x,y
Theo đề, ta có: \(9< 2x< y< 12\)
=>2x=10 và y=11
=>x=5 và y=11
d: Gọi hai số cần tìm là x,y
Theo đề, ta có: \(-15< 2x< y< -12\)
=>2x=-14 và y=-13
=>x=-7 và y=-13
Đúng 0
Bình luận (0)
 giúp mik câu c bài 3 và hết bài 4 vs ạ
giúp mik câu c bài 3 và hết bài 4 vs ạ
Bài 4:
a, F(\(x\)) = m\(x\) + 3 có nghiệm \(x\) = 2
⇔ F(2) = 0 ⇔ m.2 + 3 = 0
2m = -3
m = - \(\dfrac{3}{2}\)
b, F(\(x\)) = m\(x\) - 5 có nghiệm \(x\) = 3 ⇔ F(3) = 0
⇔3m - 5 = 0 ⇒ m = \(\dfrac{5}{3}\)
c, F(\(x\)) = \(x^2\) + a\(x\) + b có 2 nghiệm phân biệt \(x\) = 1; \(x\) = 0
⇔ \(\left\{{}\begin{matrix}0+0+b=0\\1+a+b=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}b=0\\a=-1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giúp mik giải bài 2 câu d nhanh với ạ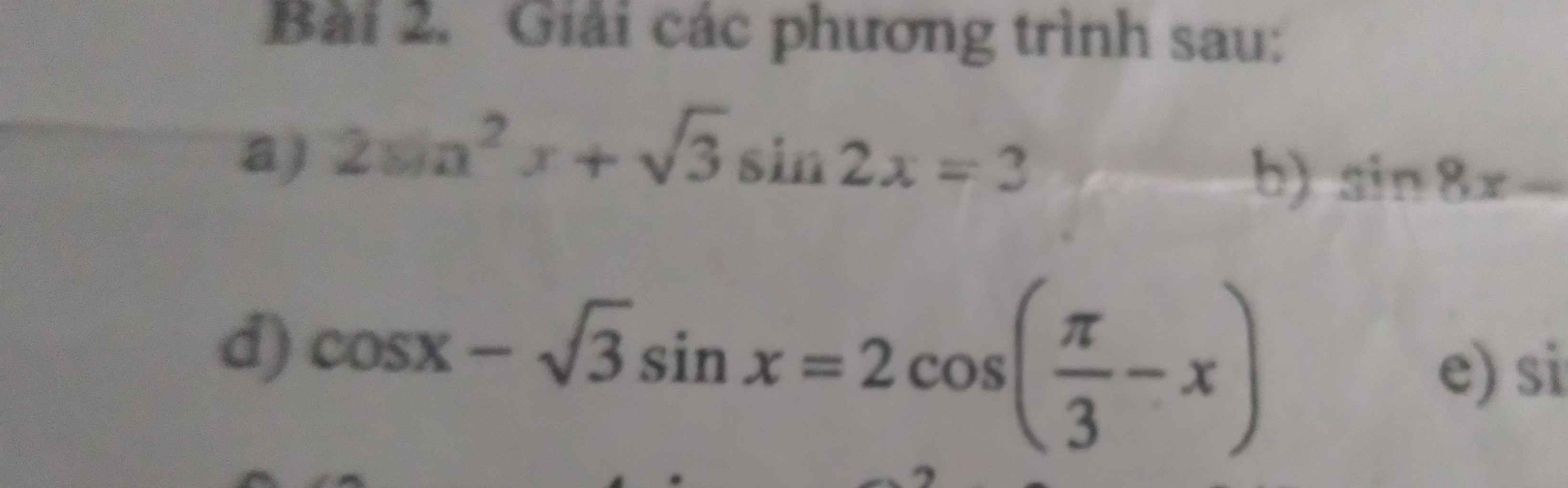
a, \(2sin^2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow-\left(1-2sin^2x\right)+\sqrt{3}sin2x=2\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
Đúng 0
Bình luận (0)
d, \(cosx-\sqrt{3}sinx=2cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow-2sin\dfrac{\pi}{3}.sinx=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
Đúng 0
Bình luận (0)
d, cosx - \(\sqrt{3}\)sinx = 2cos\(\left(\dfrac{\pi}{3}-x\right)\)
⇔ \(2cos\left(x+\dfrac{\pi}{3}\right)=2cos\left(x-\dfrac{\pi}{3}\right)\)
⇔ \(cos\left(x+\dfrac{\pi}{3}\right)-cos\left(x-\dfrac{\pi}{3}\right)\) = 0
⇔ \(-2sinx.sin\dfrac{\pi}{3}=0\)
⇔ sinx = 0
⇔ x = kπ , k ∈ Z
Sử dụng các công thức sau :
\(cos\left(x+\dfrac{\pi}{3}\right)=cosx.cos\dfrac{\pi}{3}-sinx.sin\dfrac{\pi}{3}=\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx\)
\(cosa-cosb=-2sin\dfrac{a+b}{2}.sin\dfrac{a-b}{2}\)
Đúng 0
Bình luận (0)
Giúp mik giải bài 4 vs ạ
a) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=15^2-9^2=144\)
hay AH=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{12^2}{9}=16\left(cm\right)\)
Đúng 0
Bình luận (0)
Ai giải giúp mik bài 4 vs ạ 
Bài V:
-ĐKXĐ: \(x\ne\pm1\).
\(\dfrac{m}{x-1}+\dfrac{x}{x+1}=\dfrac{x^2}{x^2-1}\)
\(\Leftrightarrow\dfrac{m\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow mx+m+x^2-x=x^2\)
\(\Leftrightarrow m\left(x+1\right)=x\)
\(\Leftrightarrow m=\dfrac{x}{x+1}\)
-Vì m,x nguyên:
\(\Rightarrow x⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1-1\right)⋮\left(x+1\right)\)
\(\Rightarrow-1⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow x\in\left\{0;-2\right\}\) (nhận)
*\(x=0\Rightarrow m=\dfrac{x}{x+1}=\dfrac{0}{0+1}=0\)
\(x=-2\Rightarrow m=\dfrac{x}{x+1}=\dfrac{-2}{-2+1}=1\)
-Vậy với \(m=0\) thì \(S=\left\{0\right\}\)
với \(m=1\) thì \(S=\left\{-2\right\}\)
Đúng 2
Bình luận (0)
/ 2x - 3 / = 3 - 2x
Các bạn ơi giải giúp mik bài này vs ạ! Đáp án của bài này là S = {x ∈ R / x =< 3/2} mà mik ko biết cách giải ạ! Ai biết giúp mik vs! Thanks nhiều!
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
Đúng 1
Bình luận (0)
 mọi người giúp mik bài 4 câu a vs ạ
mọi người giúp mik bài 4 câu a vs ạ





















