Cho hình chóp tứ giác đều S . ABCD có cạnh đáy AB = 10 cm ; cạnh bên SA = 12 cm .
Tính : a) Đường chéo AC .
b) Tính đường cao SO và thể tích hình chóp .
GIÚP ĐI MẤY BẠN MÌNH TICK CHO RỒI MÌNH KẾT BẠN NHA NHA NHA NHA :) ^_^ ........
Cho hình chóp tứ giác đều S. ABCD có độ dài cạnh bên bằng 13 cm và đáy là hình vuông có cạnh bằng 10 cm. Tính diện tích xung quanh của hình chóp
Diện tích xung quanh hình chóp là:
$\dfrac12\cdot(4\cdot10)\cdot13=260(cm^2)$
Vậy diện tích xung quanh hình chóp là $260$ cm2.
Cho hình chóp tứ giác đều S. ABCD có cạnh đáy AB=10, cạnh bên SA=12
a, Tính đường chéo AC
b. Tính đường cao SO, rồi tính thể tích của hình chóp
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB = α . Áp dụng: Tính VS ABCD . trong trường hợp α = 60 độ.
Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC =120độ . Cho SA vuông góc với đáy và SC = 2a .Tính thể tích hình chóp S.ABCD.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC=20 cm BC=15 cm AB=25 cm . Cho SA vuông góc với đáy và SA =18cm . Tính thể tích của khối chóp.
Bài 9. Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt bên SBC là tam giác đều cạnh a. Cho gócBAC =120 . Tính VS ABC .
. Bài 10. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB= BC= a . Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác S.ABC:
a.Tính thể tích khối chóp S.ABC
b.Chứng minh SC vuông góc với (AB'C')
c.Tính thể tích khối chóp S.ABC
Cho hình chóp tứ giác đều S. ABCD có cạnh đáy AB=10cm, cạnh bên SA=12cm
a) Tính đường chéo AC
b) Tính đường cao SO, rồi tính thể tích của hình chóp
a: \(AC=\sqrt{10^2+10^2}=10\sqrt{2}\left(cm\right)\)
b: AO=5căn 2(cm)
=>\(SO=\sqrt{SA^2+AO^2}=\sqrt{194}\left(cm\right)\)
Cho hình chóp tứ giác đều S. ABCD có đáy ABCD là hình vuông cạnh bằng a 3 các cạnh bên thỏa mãn SA = SB = SC =SD = a 2 . Tính thể tích khối chóp S. ABCD
A. 2 a 3 6
B. 2 a 3 2
C. 3 a 3 3
D. 6 a 3 6
cho hình chóp tứ giác đều S ABCD có đáy ABCD là hình vuông cạnh a các mặt bên tạo với mặt đáy một góc bằng 60. tính thể tích khối chóp SABCD
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 7cm và độ dài trung đoạn bằng 10 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó
Cho hình chóp tứ giác đều S. ABCD có cạnh đáy bằng 2a. Mặt bên của hình chóp tạo với mặt đáy một góc 600. Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M và N. Thể tích khối chóp S. ABMN là:
A. a 3 3 2
B. a 3 3 4
C. a 3 3 3
D. a 3 3
Chọn A
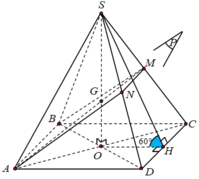
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD.
Ta có S. ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử S C D , A B C D ^ = S H O ^ = 60 o
Tam giác SHO vuông tại O có:
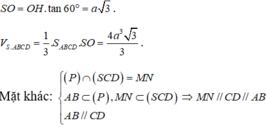
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD
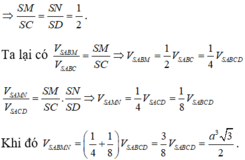
Cho hình chóp tứ giác đều S ABCD . có cạnh đáy bằng 2a . Góc giữa đường thẳng AC và mặt phẳng ( SBC) bằng 30 . Thể tích của khối chóp S ABCD bằng
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\) \(\Rightarrow SO\perp BC\)
Gọi M là trung điểm BC \(\Rightarrow OM\perp BC\)
\(\Rightarrow BC\perp\left(SOM\right)\) \(\Rightarrow\left(SBC\right)\perp\left(SOM\right)\)
Trong tam giác vuông SOM, kẻ \(OH\perp SM\)
Do SM là giao tuyến (SOM) và (SBC) \(\Rightarrow OH\perp\left(SBC\right)\)
\(\Rightarrow CH\) là hình chiếu vuông góc của OC (hay AC) lên (SBC)
\(\Rightarrow\widehat{OCH}\) là góc giữa AC và (SBC)
\(\Rightarrow\widehat{OCH}=30^0\)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\) \(\Rightarrow OH=OC.sin30^0=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng:
\(\dfrac{1}{OH^2}=\dfrac{1}{SO^2}+\dfrac{1}{OM^2}=\dfrac{1}{SO^2}+\dfrac{4}{AB^2}\Rightarrow SO=a\)
\(V=\dfrac{1}{3}SO.AB^2=\dfrac{4a^3}{3}\)