Mọi người có thể giải chi tiết giúp mình câu b và câu c được không, mình mãi không làm được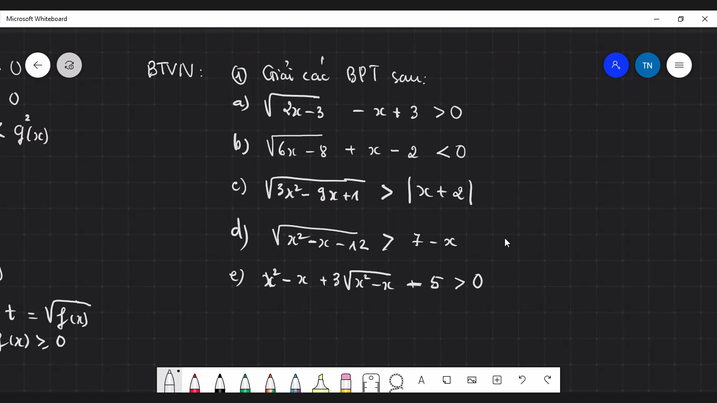

Những câu hỏi liên quan
Mọi người giúp mình 2 câu này với ạ. Mình làm mãi không được. Cảm ơn mọi người nhiều.
Câu 1:
const fi='dulieu.dat'
fo='thaythe.out'
var f1,f2:text;
a:array[1..100]of string;
n,d,i,vt:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
n:=0;
while not eof(f1) do
begin
n:=n+1;
readln(f1,a[n]);
end;
for i:=1 to n do
begin
d:=length(a[i]);
vt:=pos('anh',a[i]);
while vt<>0 do
begin
delete(a[i],vt,3);
insert('em',a[i],vt);
vt:=pos('anh',a[i]);
end;
end;
for i:=1 to n do
writeln(f2,a[i]);
close(f1);
close(f2);
end.
Đúng 1
Bình luận (0)
Câu 2:
uses crt;
const fi='mang.inp'
fo='sapxep.out'
var f1,f2:text;
a:array[1..100]of integer;
i,n,tam,j:integer;
begin
clrscr;
assign(f1,fi); rewrite(f1);
assign(f2,fo); rewrite(f2);
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(f1,a[i]:4);
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
for i:=1 to n do
write(f2,a[i]:4);
close(f1);
close(f2);
end.
Đúng 1
Bình luận (0)
Làm giúp mình với, mấy câu tính toán giải thích chi tiết ra giùm ạ chứ mình search mạng rồi nhưng không hiểu, làm được hay câu ấy

 giúp mình giải câu 1 ,2 ,3 và nhớ giải đầy đủ và chi tiết nhé không chi tiết hoặc mấy câu hồi nãy tui nói đó không làm cho vé báo cáo người ta vô coi rạp chiếu phim cho sướng
giúp mình giải câu 1 ,2 ,3 và nhớ giải đầy đủ và chi tiết nhé không chi tiết hoặc mấy câu hồi nãy tui nói đó không làm cho vé báo cáo người ta vô coi rạp chiếu phim cho sướng
đọc lại kĩ đi làm bài 1,2,3 mà làm chắc bài ba
Đúng 1
Bình luận (1)
Câu này mình đã giải được một đoạn rồi nhưng khi ra 2 TH thì không biết phân tích thế nào để chọn đáp án nữa. Hoặc cũng có thể mình sai ngay từ phương pháp làm. Rất mong mọi người giúp đỡ!Nếu có thể thì giúp mình xem luôn cách làm có gì sai không nha.Đề bài: Cho 2 axit cacboxylic mạch hở A và B (MA MB). Nếu cho hỗn hợp A và B tác dụng với Na dư được số mol H2 bằng một nửa tổng số mol A và B trong hỗn hợp, còn nếu cho hỗn hợp A và B tác dụng với nước brom dư thấy số mol Br2 đã phản ứng nhỏ hơn t...
Đọc tiếp
Câu này mình đã giải được một đoạn rồi nhưng khi ra 2 TH thì không biết phân tích thế nào để chọn đáp án nữa. Hoặc cũng có thể mình sai ngay từ phương pháp làm. Rất mong mọi người giúp đỡ!
Nếu có thể thì giúp mình xem luôn cách làm có gì sai không nha.
Đề bài: Cho 2 axit cacboxylic mạch hở A và B (MA < MB). Nếu cho hỗn hợp A và B tác dụng với Na dư được số mol H2 bằng một nửa tổng số mol A và B trong hỗn hợp, còn nếu cho hỗn hợp A và B tác dụng với nước brom dư thấy số mol Br2 đã phản ứng nhỏ hơn tổng số mol A và B trong hỗn hợp. Nếu trộn 20 gam dung dịch axit A nồng độ 23% với 50 gam dung dịch axit B nồng độ 20,64% được dung dịch D. Để trung hòa D cần vừa đủ 200 ml dung dịch NaOH 1,1M. Phát biểu đúng là:
A. A phải cho được phản ứng tráng gương.
B. B có đồng phân hình học.
C. A hoặc B là một trong 2 nguyên liệu để tổng hợp thủy tinh hữu cơ.
D. A, B hơn kém nhau một nguyên tử C trong phân tử.
Giải:
Vì: A, B tác dụng với Na thu số mol H2 bằng 1 nửa tổng số mol A, B.
⇒ A, B là axit đơn chức.
Mà: A, B cộng Br2 thì nBr2 < nA + nB
⇒ A hoặc B có liên đôi C = C trong phân tử.
Gọi: \(\left\{{}\begin{matrix}n_{C_nH_{2n+1}COOH\left(A\right)}=a\left(mol\right)\\n_{C_mH_{2m-1}COOH\left(B\right)}=b\left(mol\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}m_A=4,6\left(g\right)\Rightarrow a=\dfrac{4,6}{14n+46}\\m_B=10,32\Rightarrow b=\dfrac{10,32}{14m+44}\end{matrix}\right.\)
Mà: \(a+b=n_{NaOH}\)
\(\Rightarrow\dfrac{4,6}{14n+46}+\dfrac{10,32}{14m+44}=0,22\)
\(\Rightarrow n=\dfrac{231,84-77,28m}{43,12m-8,96}\)
Xét từng TH, ta thấy m = 2 thì n = 1 và m = 3 thì n = 0
\(\Rightarrow\left\{{}\begin{matrix}A:CH_3COOH\\B:C_2H_3COOH\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}A:HCOOH\\B:C_3H_5COOH\end{matrix}\right.\)
Vì: A, B tác dụng với Na thu số mol H2 bằng 1 nửa tổng số mol A, B.
⇒ A, B là axit đơn chức.
Mà: A, B cộng Br2 thì nBr2 < nA + nB
⇒ A hoặc B có liên đôi C = C trong phân tử.
Gọi: {nCnH2n+1COOH(A)=a(mol)nCmH2m−1COOH(B)=b(mol){nCnH2n+1COOH(A)=a(mol)nCmH2m−1COOH(B)=b(mol)
⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩mA=4,6(g)⇒a=4,614n+46mB=10,32⇒b=10,3214m+44{mA=4,6(g)⇒a=4,614n+46mB=10,32⇒b=10,3214m+44
Mà: a+b=nNaOHa+b=nNaOH
⇒4,614n+46+10,3214m+44=0,22⇒4,614n+46+10,3214m+44=0,22
⇒n=231,84−77,28m43,12m−8,96⇒n=231,84−77,28m43,12m−8,96
Xét từng TH, ta thấy m = 2 thì n = 1 và m = 3 thì n = 0
⇒{A:CH3COOHB:C2H3COOH⇒{A:CH3COOHB:C2H3COOH hoặc {A:HCOOHB:C3H5COOH
học tốt
1.Tính nhanh :7/1x5+7/5x9+7/9x13+7/13x17+7/17x21
Khó quá mình giải mãi không ra kết quả mọi người làm chi tiết giúp mình nhé ... mình cám ơn
gọi tổng này là một số A
ta có
A=7/4x(1/1x5+1/5x9+1/9x13+1/13x17+1/17x21)
A= 7/4x(1-1/5+1/5-1/9+1/9-1/13+1/13-1/17+1/17-1/21)
A= 7/4x(1-1/21)=7/4x20/21
suy ra A=5/3
Đúng 0
Bình luận (0)
7/1×5 + 7/5x9 + 7/9x13 + 7/13x17 + 7/17x21
= 7/4x(4/1x5 + 4/5x9 + 4/9x13 + 4/13x17 + 4/17x21)
= 7/4x(1 - 1/5 + 1/5 - 1/9 + 1/9 - 1/13 + 1/13 - 1/17 + 1/17 - 1/21)
= 7/4x(1-1/20)
= 7/4x19/20
= 133/80
Đúng 0
Bình luận (0)
đặt A=7/1X5+7/5X9+7/9X13+7/13X17+7/17X21
Ta có:4A=4x(7/1x5+7/5x9+7/9x13+7/13x17+7/17x21)
4A=7x(4/1x5+4/5x9+4/9x13+4/13x17+4/17x21)
4A=7x(1-1/5+1/5-1/9+1/9-1/13+1/13-1/17+1/17-1/21)
4A=7x(1-1/21)
4A=7x20/21
A=20/3:4
A=20/3 x 1/4
A=5/3
Vậy A=5/3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Đúng 1
Bình luận (1)
 Mình giải được câu a) và b) rồi . Mọi người giúp c) và d) nhé ! (Ưu tiên gải câu c , không giải câu d cũng được ) Cảm ơn!
Mình giải được câu a) và b) rồi . Mọi người giúp c) và d) nhé ! (Ưu tiên gải câu c , không giải câu d cũng được ) Cảm ơn!
Mọi người chỉ mình ạ! Bài 1: giải phương trình sqrt{5x^2}2x-1* Chỉ mình tại sao bài này nếu mà bình phương 2 vế lên có giải được ra kết quả đúng không ạ. Giair thích rõ và chi tiết giúp mình nhé * Với nhưng dạng thế nào thì có thể bình phương ạ! Bài 2: sqrt{16x+16}-sqrt{9x+9}1* Với bài này mình chưa tìm điều kiện luôn mà giải ra thành sqrt{x+1}1 rồi tìm điều kiện x+1ge0 cũng được ạ các bạn. * Nó có phụ thuộc vào dạng bài không ạ hay là chỉ có những bài mới được làm như vậy còn chỉ có những bài t...
Đọc tiếp
Mọi người chỉ mình ạ!
Bài 1: giải phương trình
\(\sqrt{5x^2}=2x-1\)
* Chỉ mình tại sao bài này nếu mà bình phương 2 vế lên có giải được ra kết quả đúng không ạ. Giair thích rõ và chi tiết giúp mình nhé
* Với nhưng dạng thế nào thì có thể bình phương ạ!
Bài 2: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
* Với bài này mình chưa tìm điều kiện luôn mà giải ra thành \(\sqrt{x+1}=1\) rồi tìm điều kiện \(x+1\ge0\) cũng được ạ các bạn.
* Nó có phụ thuộc vào dạng bài không ạ hay là chỉ có những bài mới được làm như vậy còn chỉ có những bài thì phải tìm điều kiện ngay từ đầu ạ ( và làm như vậy có bị mất trường hợp nào đi không) . giải thích tại sao
Bài 3:
Ví dụ: \(x^2\ge2x\) .
* Tại sao khi mà chia cả hai vế cho x thì chỉ nhân 1 trường hợp ( bị thiếu trường hợp). Còn khi mà chuyển vế sang cho lớn hơn hoặc bằng 0 thì lại đủ trường hợp. giải thích mình tại sao lại bị thiếu và đủ trường hợp ạ!
Giups mình đầy đủ chỗ (*) nhá!
Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.
Đúng 1
Bình luận (8)
Bài 2: ĐKXĐ luôn là thứ mà phải ghi ngay đầu bài làm để xác định được biểu thức có nghĩa. Tức là em ghi ĐKXĐ: $x+1\geq 0$ đầu tiên.
Sau đó mới giải ra $\sqrt{x+1}=1$
Đúng 1
Bình luận (2)
Xem thêm câu trả lời
TÍNH( CHỨNG MINH DẠNG TỔNG QUÁT CỦA CÂU RỒI LÀM) GIẢI CHI TIẾT TỪNG CÂU KHÔNG LÀM TẮT:
\(D=\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}+\sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}}+....+\sqrt{1+\frac{1}{99^2}+\frac{1}{100^2}}.\)
GIÚP MÌNH VỚI CÂU NÀY MÃI KHÔNG GIẢI ĐƯỢC MÀ ĐANG CẦN GẤP!!!!
Dạng tổng quát ta càn chứng minh \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{\left(a+b\right)^2}}=\frac{1}{a}+\frac{1}{b}-\frac{1}{a+b}\)
Ta có \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{\left(a+b\right)^2}}\)
\(=\sqrt{\frac{a^4+2a^3b+a^2b^2+2ab^3+b^4}{a^2b^2\left(a+b\right)^2}}\)
\(=\sqrt{\left(\frac{a^2+ab+b^2}{ab\left(a+b\right)}\right)^2}\)
\(=\frac{a^2+ab+b^2}{ab\left(a+b\right)}=\frac{1}{b}+\frac{b}{a\left(a+b\right)}=\frac{1}{b}+\frac{1}{a}-\frac{1}{a+b}\left(đpcm\right)\)
Áp dụng dạng trên ta được
\(D=1+\frac{1}{1}-\frac{1}{2}+1+\frac{1}{2}-\frac{1}{3}+1+\frac{1}{3}-\frac{1}{4}+...+1+\frac{1}{99}-\frac{1}{100}\)
\(D=100-\frac{1}{100}=\frac{9999}{100}\)
Xét biểu thức \(A=\sqrt{1+\frac{1}{a^2}+\frac{1}{\left(a+1\right)^2}}\)với a > 0
\(A^2=1+\frac{1}{a^2}+\frac{1}{\left(a+1\right)^2}=\frac{a^2\left(a+1\right)^2+\left(a+1\right)^2+a^2}{a^2\left(a+1\right)^2}=\frac{a^2\left(a^2+2a+1+1\right)+\left(a+1\right)^2}{a^2\left(a+1\right)^2}=\frac{a^4+2a^2\left(a+1\right)+\left(a+1\right)^2}{a^2\left(a+1\right)^2}=\frac{\left(a^2+a+1\right)^2}{a^2\left(a+1\right)^2}=\left[\frac{a^2+a+1}{a\left(a+1\right)}\right]^2\)Do a > 0 nên A > 0 và \(A=\frac{a^2+a+1}{a\left(a+1\right)}=1+\frac{1}{a\left(a+1\right)}=1+\frac{1}{a}-\frac{1}{a+1}\)
Do đó \(D=\left(1+\frac{1}{1}-\frac{1}{2}\right)+\left(1+\frac{1}{2}-\frac{1}{3}\right)+\left(1+\frac{1}{3}-\frac{1}{4}\right)+...+\left(1+\frac{1}{99}-\frac{1}{100}\right)=99+\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}\right)=100-\frac{1}{100}=99,99\)




















