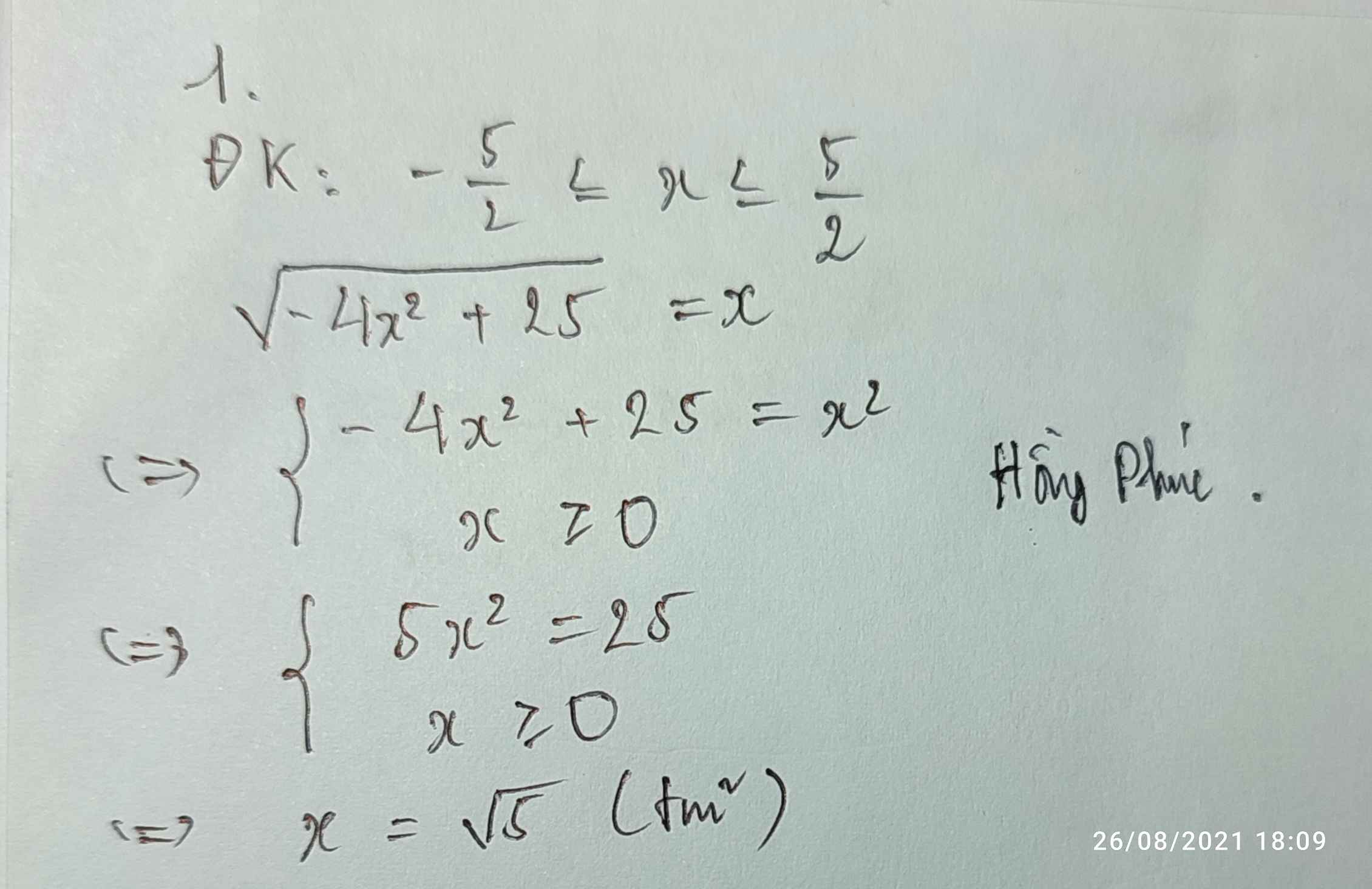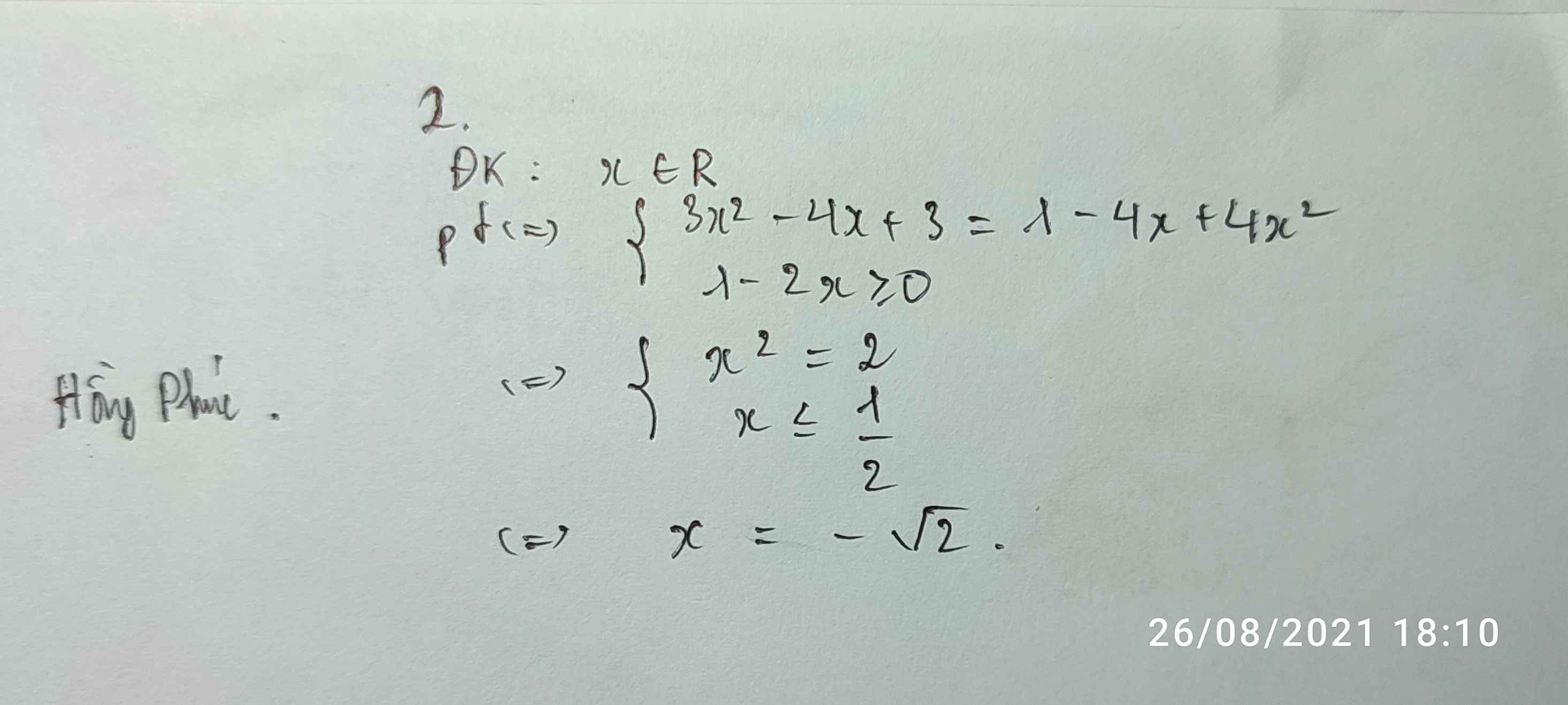\(x-1-2-3-4=0\sqrt{\sqrt[]{}\dfrac{ }{ }}\)

Những câu hỏi liên quan
1.\(\sqrt{-4x^2+25}=x\)
2.\(\sqrt{3x^2-4x+3}=1-2x\)
3. \(\sqrt{4\left(1-x\right)^2}-\sqrt{3}=0\)
4.\(\dfrac{3\sqrt{x+5}}{\sqrt{ }x-1}< 0\)
5. \(\dfrac{3\sqrt{x-5}}{\sqrt{x+1}}\ge0\)
a \(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9x-45}=4\)
b \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}=4\)
c \(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}=-4}\)
d \(\sqrt{9x+27}+4\sqrt{x+3}-\dfrac{3}{4}\sqrt{16x+48}=0\)
a: ĐKXĐ: x-5>=0
=>x>=5
\(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\cdot\sqrt{9x-45}=4\)
=>\(2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\)
=>\(2\sqrt{x-5}=4\)
=>x-5=4
=>x=9(nhận)
b: ĐKXĐ: x-1>=0
=>x>=1
\(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}=4\)
=>\(\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}=4\)
=>\(-2\sqrt{x-1}=4\)
=>\(\sqrt{x-1}=-2\)(vô lý)
Vậy: Phương trình vô nghiệm
c: ĐKXĐ: x-2>=0
=>x>=2
\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\cdot\sqrt{9x-18}+6\cdot\sqrt{\dfrac{x-2}{81}}=-4\)
=>\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\cdot3\sqrt{x-2}+6\cdot\dfrac{\sqrt{x-2}}{9}=-4\)
=>\(\sqrt{x-2}\left(\dfrac{1}{3}-2+\dfrac{2}{3}\right)=-4\)
=>\(-\sqrt{x-2}=-4\)
=>x-2=16
=>x=18(nhận)
d: ĐKXĐ: x+3>=0
=>x>=-3
\(\sqrt{9x+27}+4\sqrt{x+3}-\dfrac{3}{4}\cdot\sqrt{16x+48}=0\)
=>\(3\sqrt{x+3}+4\sqrt{x+3}-\dfrac{3}{4}\cdot4\sqrt{x+3}=0\)
=>\(4\sqrt{x+3}=0\)
=>x+3=0
=>x=-3(nhận)
Đúng 1
Bình luận (0)
a) \(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9x-45}=4\)
= \(2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9\left(x-5\right)}=4\)
= \(2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\)
= \(2\sqrt{x-5}=4\)
= \(\sqrt{x-5}=2\)
= \(\left|x-5\right|=4\)
=> \(x-5=\pm4\)
\(x=\pm4+5\)
\(x=9;x=1\)
Vậy x=9; x=1
Đúng 1
Bình luận (0)
b) \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}=4\)
\(\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}=4\)
\(-2\sqrt{x-1}=4\)
\(\sqrt{x-1}=-2\)
=>\(\left|x-1\right|=-2\)
\(x-1=\mp2\)
\(x=-3;x=1\)
Vậy x=-3; x=1
Đúng 0
Bình luận (0)
Tìm x
a)\(2\sqrt{2}-\dfrac{1}{2}.\sqrt{x}=0\)
b)\(2.\sqrt{x}-\sqrt{\dfrac{x}{3}}=1\)
c)\(4.\sqrt{x}+\sqrt{\dfrac{x}{2}}=\dfrac{1}{3}\)
a: Ta có: \(2\sqrt{2}-\dfrac{1}{2}\cdot\sqrt{x}=0\)
\(\Leftrightarrow\sqrt{x}\cdot\dfrac{1}{2}=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{x}=4\sqrt{2}\)
hay x=32
b: Ta có: \(2\sqrt{x}-\sqrt{\dfrac{x}{3}}=1\)
\(\Leftrightarrow2\sqrt{x}-\dfrac{\sqrt{3}}{3}\sqrt{x}=1\)
\(\Leftrightarrow\sqrt{x}=\dfrac{6+\sqrt{3}}{11}\)
hay \(x=\dfrac{39+12\sqrt{3}}{121}\)
c: Ta có: \(4\sqrt{x}+\sqrt{\dfrac{x}{2}}=\dfrac{1}{3}\)
\(\Leftrightarrow4\sqrt{x}+\dfrac{\sqrt{2}}{2}\sqrt{x}=\dfrac{1}{3}\)
\(\Leftrightarrow\sqrt{x}=\dfrac{8-\sqrt{2}}{93}\)
hay \(x=\dfrac{66-16\sqrt{2}}{8649}\)
Đúng 0
Bình luận (0)
a : dfrac{3}{sqrt{x}-5}+dfrac{20-2sqrt{x}}{x-25}với x ≥ 0 x ≠ 25b : dfrac{sqrt{x}}{sqrt{x}-3}+dfrac{2sqrt{x}-2}{x-9}với x ≥ 0 x ≠ 9c : dfrac{sqrt{x}-1}{sqrt{x}+2}+dfrac{5sqrt{x}-2}{x-4}với x ≥ 0 x ≠ 4d : left(dfrac{x-2}{x+2sqrt{x}}+dfrac{1}{sqrt{x}+2}right).dfrac{sqrt{x}+1}{sqrt{x}-1}với ≥ 0 x ≠ 1
Đọc tiếp
a : \(\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{x-25}\)với x ≥ 0 x ≠ 25
b : \(\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\)với x ≥ 0 x ≠ 9
c : \(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{x-4}\)với x ≥ 0 x ≠ 4
d : \(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)với ≥ 0 x ≠ 1
\(a,\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{x-25}\\ =\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\\ =\dfrac{3\left(\sqrt{x}+5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}+\dfrac{20-2\sqrt{x}}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\\ =\dfrac{3\sqrt{x}+15+20-2\sqrt{x}}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\\ =\dfrac{\sqrt{x}+35}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\)
Đúng 0
Bình luận (0)
\(b,\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\\ =\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x-9}+\dfrac{2\sqrt{x}-2}{x-9}\\ =\dfrac{x+3\sqrt{x}+2\sqrt{x}-2}{x-9}\\ =\dfrac{x-5\sqrt{x}-2}{x-9}\)
Đúng 0
Bình luận (0)
a: \(\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{x-25}\)
\(=\dfrac{3\sqrt{x}+15+20-2\sqrt{x}}{x-25}=\dfrac{\sqrt{x}+35}{x-25}\)
b: \(\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\)
\(=\dfrac{x+3\sqrt{x}+2\sqrt{x}-2}{x-9}=\dfrac{x+5\sqrt{x}-2}{x-9}\)
c: \(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{x-4}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{x-4}\)
\(=\dfrac{x-3\sqrt{x}+2+5\sqrt{x}-2}{x-4}=\dfrac{x+2\sqrt{x}}{x-4}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
d: \(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{x-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình sau:1) sqrt{3x^2+5x+8}-sqrt{3x^2+5x+1}12) x^2-2x-12+4sqrt{left(4-xright)left(2+xright)}03) 3sqrt{x}+dfrac{3}{2sqrt{x}}2x+dfrac{1}{2x}-74) sqrt{x}-dfrac{4}{sqrt{x+2}}+sqrt{x+2}05)left(x-7right)sqrt{dfrac{x+3}{x-7}}x+46) 2sqrt{x-4}+sqrt{x-1}sqrt{2x-3}+sqrt{4x-16}7) sqrt{x+2sqrt{x-1}}+sqrt{x-2sqrt{x-1}}dfrac{x+3}{2}Giúp mình với ajk, mink đang cần gấp
Đọc tiếp
Giải các phương trình sau:
1) \(\sqrt{3x^2+5x+8}-\sqrt{3x^2+5x+1}=1\)
2) \(x^2-2x-12+4\sqrt{\left(4-x\right)\left(2+x\right)}=0\)
3) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}=2x+\dfrac{1}{2x}-7\)
4) \(\sqrt{x}-\dfrac{4}{\sqrt{x+2}}+\sqrt{x+2}=0\)
5)\(\left(x-7\right)\sqrt{\dfrac{x+3}{x-7}}=x+4\)
6) \(2\sqrt{x-4}+\sqrt{x-1}=\sqrt{2x-3}+\sqrt{4x-16}\)
7) \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=\dfrac{x+3}{2}\)
Giúp mình với ajk, mink đang cần gấp
a : dfrac{x}{x-4}+dfrac{1}{sqrt{x}-2}+dfrac{1}{sqrt{x}+2}với a ≥ 0 x ≠ 4 b : left(dfrac{1}{sqrt{x}}+dfrac{sqrt{x}}{sqrt{x}+1}right).dfrac{sqrt{x}}{x+sqrt{x}}c : dfrac{sqrt{x}}{sqrt{x}-1}+dfrac{3}{sqrt{x}+1}-dfrac{6sqrt{x}-4}{x-1}d : left[dfrac{a+3sqrt{a}+2}{left(sqrt{a}+2right)left(sqrt{a}-1right)}-dfrac{asqrt{a}}{a-1}right]:left(dfrac{1}{sqrt{a}-1}+dfrac{1}{sqrt{a}+1}right)
Đọc tiếp
a : \(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)với a ≥ 0 x ≠ 4
b : \(\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right).\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
c : \(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{x-1}\)
d : \(\left[\dfrac{a+3\sqrt{a}+2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}-\dfrac{a\sqrt{a}}{a-1}\right]:\left(\dfrac{1}{\sqrt{a}-1}+\dfrac{1}{\sqrt{a}+1}\right)\)
a) \(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\) \(\left(x\ge0;x\ne4\right)\)
\(=\dfrac{x}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
b) \(\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot\dfrac{\sqrt{x}}{x+\sqrt{x}}\) (\(x>0\))
\(=\left[\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]\cdot\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)^2}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(x+2\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{x\sqrt{x}+2x+\sqrt{x}}\)
Đúng 1
Bình luận (0)
c) \(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{3}{\sqrt{x}+1}-\dfrac{6\sqrt{x}-4}{x-1}\) (\(x\ge0;x\ne1\))
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{6\sqrt{x}-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
d) \(\left[\dfrac{a+3\sqrt{a}+2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}-\dfrac{a\sqrt{a}}{a-1}\right]:\left(\dfrac{1}{\sqrt{a}-1}+\dfrac{1}{\sqrt{a}+1}\right)\) \(\left(a\ne1;a\ge0\right)\)
\(=\left[\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}-\dfrac{a\sqrt{a}}{a-1}\right]:\dfrac{\sqrt{a}+1+\sqrt{a}-1}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{\left(\sqrt{a}+1\right)^2-a\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}:\dfrac{2\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{a+2\sqrt{a}+1-a\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{2\sqrt{a}}\)
\(=\dfrac{a-a\sqrt{a}+2\sqrt{a}+1}{2\sqrt{a}}\)
Đúng 1
Bình luận (0)
Rút gọn:
A= \(\dfrac{10\sqrt{x}}{x+3\sqrt{x}-4}\) - \(\dfrac{2\sqrt{x}-3}{\sqrt{x}+4}\) + \(\dfrac{\sqrt{x}+1}{1-\sqrt{x}}\) ( với x ≥ 0; x ≠ 1)
Với `x >= 0,x ne 1` có:
`A=[10\sqrt{x}]/[(\sqrt{x}-1)(\sqrt{x}+4)]-[2\sqrt{x}-3]/[\sqrt{x}+4]-[\sqrt{x}+1]/[\sqrt{x}-1]`
`A=[10\sqrt{x}-(2\sqrt{x}-3)(\sqrt{x}-1)-(\sqrt{x}+1)(\sqrt{x}+4)]/[(\sqrt{x}-1)(\sqrt{x}+4)]`
`A=[10\sqrt{x}-2x+2\sqrt{x}+3\sqrt{x}-3-x-4\sqrt{x}-\sqrt{x}-4]/[(\sqrt{x}-1)(\sqrt{x}+4)]`
`A=[-3x+10\sqrt{x}-7]/[(\sqrt{x}-1)(\sqrt{x}+4)]`
`A=[(\sqrt{x}-1)(-3\sqrt{x}-7)]/[(\sqrt{x}-1)(\sqrt{x}+4)]`
`A=[-3\sqrt{x}-7]/[\sqrt{x}+4]`
Đúng 1
Bình luận (0)
( \(\dfrac{\sqrt{x}}{\sqrt{x}-2}\) + \(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\) - \(\dfrac{3\sqrt{x}+2}{x-4}\) ) : \(\dfrac{\sqrt{x}-2}{x-4}\) ( với x ≥ 0; x ≠ 4)
RÚT GỌN Ạ
Với \(x\ge0;x\ne4\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)+\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{x-4}{\sqrt{x}-2}\)
\(=\dfrac{x+2\sqrt{x}+x-2\sqrt{x}-\sqrt{x}-2-3\sqrt{x}+2}{x-4}.\dfrac{x-4}{\sqrt{x}-2}\)
\(=\dfrac{2x-4\sqrt{x}}{x-4}.\dfrac{x-4}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}-2}=2\sqrt{x}\)
Đúng 2
Bình luận (0)
(\(\dfrac{\sqrt{x}}{\sqrt{x}-2}\) + \(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)-\(\dfrac{3\sqrt{x}+2}{x-4}\) ) : \(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\) ( với x ≥ 0; x ≠ 4)
RÚT GỌN Ạ
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)+\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)-3\sqrt{x}-2}{x-4}\right):\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\\ =\dfrac{x+2\sqrt{x}+x-\sqrt{x}-2\sqrt{x}+2-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\times\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\\ =\dfrac{2x-4\sqrt{x}}{\sqrt{x}-2}\times\dfrac{1}{\sqrt{x}-2}\\ =\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}-2}\times\dfrac{1}{\sqrt{x}-2}=\dfrac{2\sqrt{x}}{\sqrt{x}-2}\)
Đúng 2
Bình luận (0)
CM:
\(\dfrac{3}{2}\sqrt{6}+2\sqrt{\dfrac{2}{3}}-4\sqrt{\dfrac{3}{4}}=\dfrac{\sqrt{6}}{6}\)
\(\dfrac{x\sqrt{y}+y\sqrt{x}}{\sqrt{xy}}:\dfrac{1}{\sqrt{x}+\sqrt{y}}=x-y\) với x.0, y>0, x≠y
\(\dfrac{\sqrt{y}}{x-\sqrt{xy}}+\dfrac{\sqrt{x}}{y-\sqrt{xy}}=\dfrac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\)với x>0, y>0, x≠y
a: \(=\dfrac{3}{2}\sqrt{6}+\dfrac{2}{3}\sqrt{6}-2\sqrt{3}=\dfrac{13}{6}\sqrt{6}-2\sqrt{3}\)
b: \(VT=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\cdot\left(\sqrt{x}+\sqrt{y}\right)=\left(\sqrt{x}+\sqrt{y}\right)^2\)
c: \(VT=\dfrac{\sqrt{y}}{\sqrt{x}\left(\sqrt{x}-\sqrt{y}\right)}+\dfrac{\sqrt{x}}{\sqrt{y}\left(\sqrt{y}-\sqrt{x}\right)}\)
\(=\dfrac{y-x}{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}=\dfrac{-\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)
Đúng 0
Bình luận (0)