Những câu hỏi liên quan
Bài 15: Cho AABC có AB = 5 cm; AC = 12 cm ; BC = 13 cm a) Chứng minh AABC vuông tại A và tính độ dài đường cao AH;b) Kẻ HEl AB tại E, HF perp AC tại F. Chứng minh: AE.AB=AF.AC c) Chứng minh: A AEF và AABC đồng dạng.
Bài 1.0. Cho AABC có AB = 48cm; BC=36 cm; CA= 64 cm. lấy E ∈ AC sao cho AE= 24 cm; trên AB lấy D sao cho AD=32. a. So sánh AABC và AADE b, Tính DE c, gọi F là giao điểm của BC và DE. Tính DF
bài 2
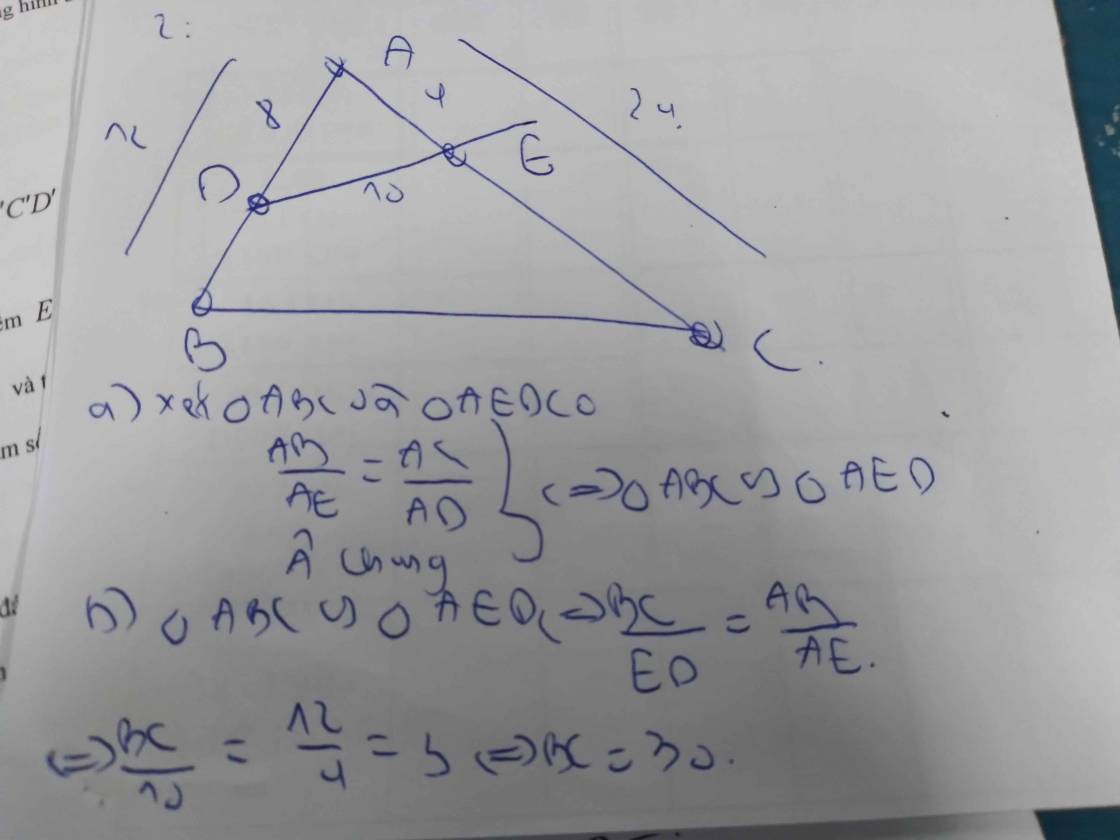
Bài 1.2. Cho AABC có AB = 12 ; AC = 24 Trên AB và AC lấy các điểm D và E sao cho AD = 8 ; A E = 4va DE = 10 Chứng minh rằng: a) tam giác ABC đồng giạng tam giác AED (g-g)
b) Tính BC
a) Ta có :
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA\)
\(S_{ADE}=\dfrac{1}{2}AD.AE.sinA\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\dfrac{AB.AC}{AD.AE}=\dfrac{48.64}{32.24}=4\)
\(\Rightarrow S_{ABC}=4S_{ADE}\)
b) Xét \(\Delta ABC\) ta có :
\(p=\left(AB+AC+BC\right):2=\left(48+36+64\right):2=74\left(cm\right)\)
Theo công thức Heron :
\(S_{ABC}=\sqrt[]{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74\left(74-48\right)\left(74-64\right)\left(74-36\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74.26.10.38}=4\sqrt[]{5.13.19.37}=4\sqrt[]{45695}\left(cm^2\right)\)
\(\Rightarrow S_{ADE}=\dfrac{S_{ABC}}{4}=\dfrac{4\sqrt[]{45695}}{4}=\sqrt[]{45695}\left(cm^2\right)\)
Xét \(\Delta ADE\) ta có :
Đặt \(DE=x\left(x>0\right)\)
\(p=\dfrac{\left(AD+AE+x\right)}{2}=\dfrac{\left(32+24+x\right)}{2}=\dfrac{56+x}{2}=28+\dfrac{x}{2}\left(cm\right)\)
\(S_{ADE}=\sqrt[]{p\left(p-AD\right)\left(p-AE\right)\left(p-DE\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(28+\dfrac{x}{2}-32\right)\left(28+\dfrac{x}{2}-24\right)\left(28+\dfrac{x}{2}-x\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)}\)
\(\Rightarrow S^2_{ADE}=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow45695=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow5.13.19.37=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\left(1\right)\)
Ta thấy khi \(x=18\) thì vế phải có :
\(\left\{{}\begin{matrix}\dfrac{x}{2}-4=5\\\dfrac{x}{2}+4=13\\28-\dfrac{x}{2}=19\\28+\dfrac{x}{2}=37\end{matrix}\right.\) \(\Rightarrow x=18\) pt (1) thỏa
Vậy \(DE=18\left(cm\right)\)
Đúng 3
Bình luận (0)
Vẽ cả hình giúp mình với ạ!
Bài 1: Cho AABC nhọn, có AB 6cm, AC 12cm, BD 5cm. AD là đường phân giác của BAC
a) Tính DC và BC
b) Kê DK // AC, (K AB), tính DK.
c) Cm ABDK - ABCA
Bài 2: Cho AABC, có AB 8cm, AC 10cm, DC Sem. AD là đường phân giác của BAC. c) Cm ACDH - ACBA
a) Tính DB và BC
b) Ke DH // AB, (He AC), tỉnh DH.
Bài 3: Cho tam giác vuông ABC (A 90°) có AB 9cm, AC 12cm. Tia phân giác góc A cắt BC tại D.Từ D kẻ DE vuông góc với AC (E thuộc AC). Tính độ dài các đoạn thẳng BD,CD...
Đọc tiếp
Vẽ cả hình giúp mình với ạ!
Bài 1: Cho AABC nhọn, có AB = 6cm, AC = 12cm, BD= 5cm. AD là đường phân giác của BAC
a) Tính DC và BC
b) Kê DK // AC, (K AB), tính DK.
c) Cm ABDK - ABCA
Bài 2: Cho AABC, có AB= 8cm, AC = 10cm, DC= Sem. AD là đường phân giác của BAC. c) Cm ACDH - ACBA
a) Tính DB và BC
b) Ke DH // AB, (He AC), tỉnh DH.
Bài 3: Cho tam giác vuông ABC (A = 90°) có AB = 9cm, AC = 12cm. Tia phân giác góc A cắt BC tại D.Từ D kẻ DE vuông góc với AC (E thuộc AC). Tính độ dài các đoạn thẳng BD,CD và DE
Bài 1:
a) Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
\(\Leftrightarrow\dfrac{6}{5}=\dfrac{12}{CD}\)
hay CD=10(cm)
Ta có: BD+CD=BC(D nằm giữa B và C)
nên BC=10+5=15(cm)
Vậy: DC=10cm; BC=15cm
Đúng 2
Bình luận (0)
Cho AABC vuông tai A, có AB = 5cm, AC = 12cm. Tia phân giác góc A cắt BC tại D, từ D kė DE I AC(E e AC). a) Tính độ dài BD và CD. b) Chứng minh: AABC AEDC.
a: BC=căn 5^2+12^2=13cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/5=CD/12=(BD+CD)/(5+12)=13/17
=>BD=65/17cm; CD=156/17cm
b: Xét ΔCED vuông tại E và ΔCAB vuông tại A có
góc C chung
=>ΔCED đồng dạng với ΔCAB
Đúng 0
Bình luận (0)
Cho AABC vuông tại A (AB AC) có phân giác AD (DE BC). Kẻ DE vuônggóc với AC tại E (E e AC).1) Chứng minh: Tứ giác ABDE là hình thang và tam giác ABC đồng dạng với tam giác EDC.2) Nếu cho biết AB 9cm, BC 15cm, hãy tính: diện tích AABC và độ dài đoạn thẳng DE .3) Gọi M là trung điểm của cạnh AB. Chứng minh CM đi qua trung điểm của đoạn thẳng DEcứu mik vs gấp lắm rồi !!!!!!!!!!!!!
Đọc tiếp
Cho AABC vuông tại A (AB < AC) có phân giác AD (DE BC). Kẻ DE vuông
góc với AC tại E (E e AC).
1) Chứng minh: Tứ giác ABDE là hình thang và tam giác ABC đồng dạng với tam giác EDC.
2) Nếu cho biết AB = 9cm, BC = 15cm, hãy tính: diện tích AABC và độ dài đoạn thẳng DE .
3) Gọi M là trung điểm của cạnh AB. Chứng minh CM đi qua trung điểm của đoạn thẳng DE
cứu mik vs gấp lắm rồi !!!!!!!!!!!!!
1: Xét tứ giác ABDE có
DE//AB
góc EAB=90 độ
=>ABDE là hình thang vuông
XétΔCED vuông tại E và ΔCAB vuông tại A có
góc C chung
=>ΔCED đồng dạng với ΔCAB
2: AC=căn 15^2-9^2=12cm
S ABC=1/2*AB*AC=1/2*12*9=54cm2
Xét ΔABC có AD là phân giác
nên BD/CD=AB/AC=3/4
=>CD/BD=4/3
=>CD/BC=4/7
ΔCED đồng dạng với ΔCAB
=>ED/AB=CD/CB=4/7
=>ED=9*4/7=36/7cm
3: Gọi giao của CM với ED làI
Xét ΔCAM có EI//AM
nên EI/AM=CI/CM
Xét ΔCMB có ID//MB
nên ID/MB=CI/CM
=>EI/AM=ID/MB
mà AM=MB
nên EI=ID
=>I là trung điểm của ED
Đúng 0
Bình luận (0)
Bài 2: Cho AABC có Â = 62°, các đường phân giác BD và CE cắt nhau tại I.
a) Tính BIC
b) Tính BAI
c) Chứng minh điểm I cách đều ba cạnh của AABC
a: \(\widehat{ABC}+\widehat{ACB}=180^0-62^0=118^0\)
=>\(\widehat{IBC}+\widehat{ICB}=59^0\)
hay \(\widehat{BIC}=121^0\)
b: Xét ΔABC có
BD là phân giác
CE là phân giác
BD cắt CE tại I
Do đó: I là tâm đường tròn nội tiếp
=>AI là tia phân giác của góc BAC
=>\(\widehat{BAI}=31^0\)
Đúng 2
Bình luận (0)
Bài 1
a) Cho AABC cân tại A có A = 75°, tính B?
b) Biết AMNK cân tại N có K = 50°, tính N?
Bài 2
Cho hình vẽ biết AB = 9cm; AC = 12cm
a) Tính BC?
b) Biết BH = 5cm. Tính AH?
Bài 3:Cho AABC cân tại A, vẽ AH 1 BC (H e BC)
a) Chứng minh AAHB=AAHC
b) Vẽ HM 1 AB (M e AB), HN I AC (N e AC). Chứng minh HM = HN
c) Chứng minh AAMN cân
d) Chứng minh AH? + BM² = AN² + BH?
Cho AABC vuông tại A có AB = 12cm BC = 20cm và AH là đường ca a) Tính độ dài các cạnh AH, BH và CH của AABC. b) Giải tam giác vuông trên (số đo của góc làm tròn đến độ). c) Chứng minh rằng: AB. cos B + AC cosC = BC
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+12^2=20^2\)
=>\(AC^2=400-144=256\)
=>\(AC=\sqrt{256}=16\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>\(AH\cdot20=12\cdot16=192\)
=>AH=9,6(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{12^2}{20}=7,2\left(cm\right)\\CH=\dfrac{16^2}{20}=12,8\left(cm\right)\end{matrix}\right.\)
b: XétΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
c: \(AB\cdot cosB+AC\cdot cosC\)
\(=AB\cdot\dfrac{AB}{BC}+AC\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB^2+AC^2}{BC}=\dfrac{BC^2}{BC}=BC\)
Đúng 0
Bình luận (0)
Bài 6: (3,5 điểm) Cho AABC vuông tại A, có AC 5 cm, BC 13 cm. a) Tính AB và so sánh hai góc ABC và góc ACB b) Trên tia đổi của tia AC, vẽ điểm D sao cho A là trung điểm của CD. Chứng minh: AABC AABD c) Vẽ điểm K là trung điểm của BC. Gọi G là giao điểm của AB và DK. Chứng minh BG 2GA. d) Gọi H là trung điểm của AD. Qua H vẽ đường thẳng vuông góc với AD cắt BD tại E. Chứng minh 3 điểm E, G, C thắng hàng.
Đọc tiếp
Bài 6: (3,5 điểm) Cho AABC vuông tại A, có AC = 5 cm, BC = 13 cm. a) Tính AB và so sánh hai góc ABC và góc ACB b) Trên tia đổi của tia AC, vẽ điểm D sao cho A là trung điểm của CD. Chứng minh: AABC= AABD c) Vẽ điểm K là trung điểm của BC. Gọi G là giao điểm của AB và DK. Chứng minh BG = 2GA. d) Gọi H là trung điểm của AD. Qua H vẽ đường thẳng vuông góc với AD cắt BD tại E. Chứng minh 3 điểm E, G, C thắng hàng.
a: AB=12cm
Xét ΔABC có AC<AB
nên \(\widehat{ABC}< \widehat{ACB}\)
b: Xét ΔABC vuông tại A vàΔABD vuông tại A có
AB chung
AC=AD
DO đó: ΔABC=ΔABD
c: Xét ΔBDC có
AB là đường trung tuyến
DK là đường trung tuyến
BA cắt DK tại G
Do đó: G là trọng tâm
=>BG=2GA
Đúng 1
Bình luận (0)