Bài 1:
a) Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
\(\Leftrightarrow\dfrac{6}{5}=\dfrac{12}{CD}\)
hay CD=10(cm)
Ta có: BD+CD=BC(D nằm giữa B và C)
nên BC=10+5=15(cm)
Vậy: DC=10cm; BC=15cm
Bài 1:
a) Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)
\(\Leftrightarrow\dfrac{6}{5}=\dfrac{12}{CD}\)
hay CD=10(cm)
Ta có: BD+CD=BC(D nằm giữa B và C)
nên BC=10+5=15(cm)
Vậy: DC=10cm; BC=15cm
Cho hình chóp tam giác đều S.ABC có cạnh đáy AB=12cm, cạnh bên SA=10cm. Tính diện tích xung quanh của hình chóp đều đó
Tính diện tích xung quanh, toàn phần, thể tích của hình chóp tứ giác có h= SH=a√2,a=AB=BC=a
cho hình chóp đều S.ABC có đáy là hình tam giác đều cạnh 6cm ,cạnh bên 5cm a, Tính Sxung quanh b,thể tích =?
Hình chóp đều có đáy abc là tam giác đều biết ab= 6cm sa=5cm. diện tích xung quanh chóp là
a 30cm^2
b36cm^2
c72cm^2
d45cm^2
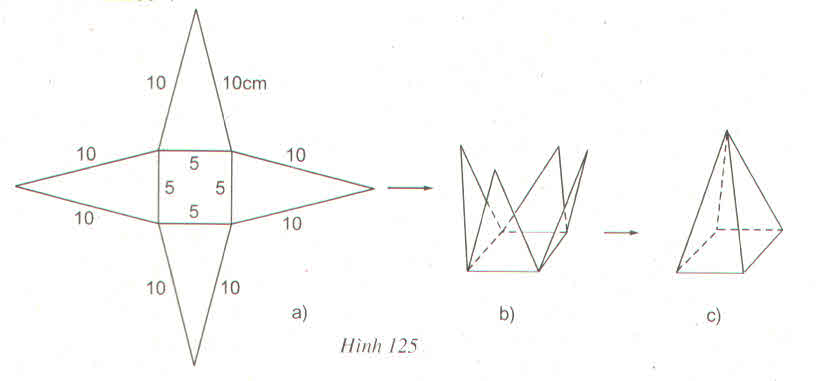
Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau ?
b) Sử dụng định lí Pi-ta-go để tính chiều cao ứng với đáy của mỗi tam giác
c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu ?
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25 cm, đáy là hình vuông ABCD cạnh 30 cm
Tính diện tích toàn phần của hình chóp.
Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên hình 125

Hình chóp đều S.ABC có cạnh đáy \(a=12cm\), chiều cao h = 8cm. Hãy tính diện tích xung quanh của hình chóp đó ?