Bài 1.0. Cho AABC có AB = 48cm; BC=36 cm; CA= 64 cm. lấy E ∈ AC sao cho AE= 24 cm; trên AB lấy D sao cho AD=32. a. So sánh AABC và AADE b, Tính DE c, gọi F là giao điểm của BC và DE. Tính DF
bài 2
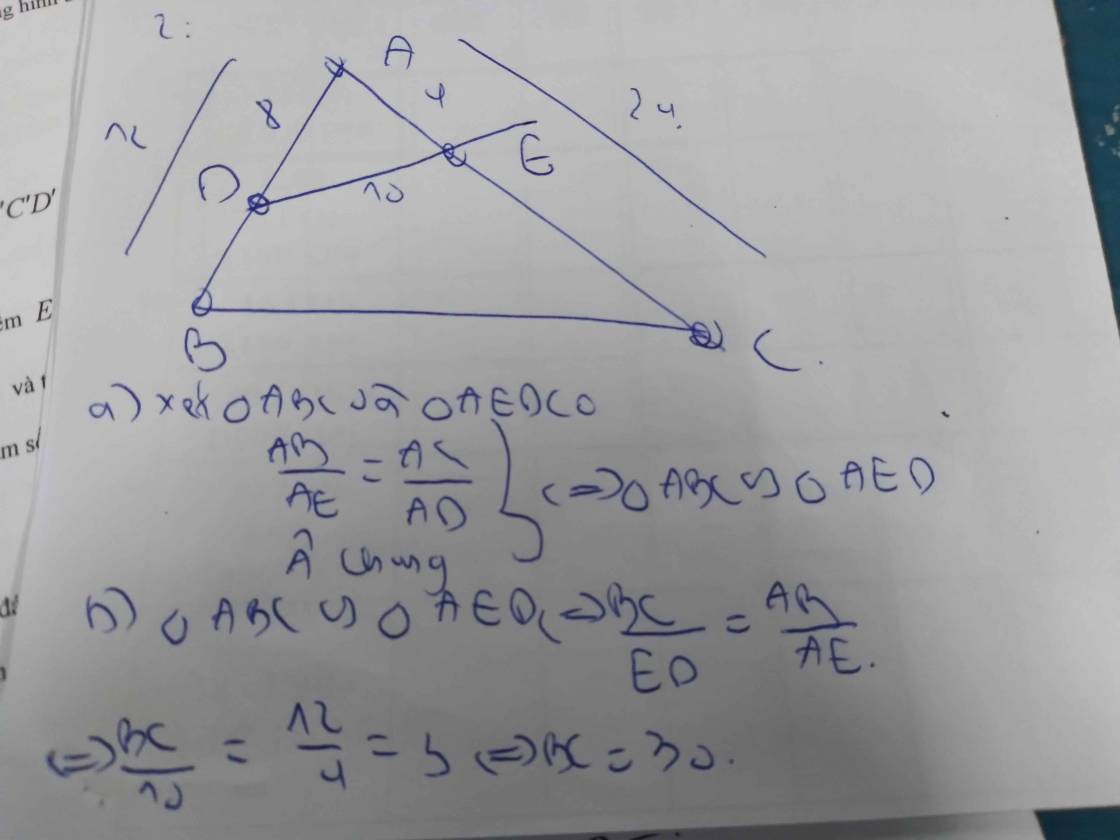
Bài 1.2. Cho AABC có AB = 12 ; AC = 24 Trên AB và AC lấy các điểm D và E sao cho AD = 8 ; A E = 4va DE = 10 Chứng minh rằng: a) tam giác ABC đồng giạng tam giác AED (g-g)
b) Tính BC
a) Ta có :
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA\)
\(S_{ADE}=\dfrac{1}{2}AD.AE.sinA\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\dfrac{AB.AC}{AD.AE}=\dfrac{48.64}{32.24}=4\)
\(\Rightarrow S_{ABC}=4S_{ADE}\)
b) Xét \(\Delta ABC\) ta có :
\(p=\left(AB+AC+BC\right):2=\left(48+36+64\right):2=74\left(cm\right)\)
Theo công thức Heron :
\(S_{ABC}=\sqrt[]{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74\left(74-48\right)\left(74-64\right)\left(74-36\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74.26.10.38}=4\sqrt[]{5.13.19.37}=4\sqrt[]{45695}\left(cm^2\right)\)
\(\Rightarrow S_{ADE}=\dfrac{S_{ABC}}{4}=\dfrac{4\sqrt[]{45695}}{4}=\sqrt[]{45695}\left(cm^2\right)\)
Xét \(\Delta ADE\) ta có :
Đặt \(DE=x\left(x>0\right)\)
\(p=\dfrac{\left(AD+AE+x\right)}{2}=\dfrac{\left(32+24+x\right)}{2}=\dfrac{56+x}{2}=28+\dfrac{x}{2}\left(cm\right)\)
\(S_{ADE}=\sqrt[]{p\left(p-AD\right)\left(p-AE\right)\left(p-DE\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(28+\dfrac{x}{2}-32\right)\left(28+\dfrac{x}{2}-24\right)\left(28+\dfrac{x}{2}-x\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)}\)
\(\Rightarrow S^2_{ADE}=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow45695=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow5.13.19.37=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\left(1\right)\)
Ta thấy khi \(x=18\) thì vế phải có :
\(\left\{{}\begin{matrix}\dfrac{x}{2}-4=5\\\dfrac{x}{2}+4=13\\28-\dfrac{x}{2}=19\\28+\dfrac{x}{2}=37\end{matrix}\right.\) \(\Rightarrow x=18\) pt (1) thỏa
Vậy \(DE=18\left(cm\right)\)