Đường thẳng y=(2m+3)x+7 và đường thẳng y=(4m+7)x-½ Song song với nhau khi m có giá trị bằng ...

Những câu hỏi liên quan
Câu 3:Cho đường thẳng (d1):y=(m-1)x+4.Tìm giá trị của m để:
a)Đường thẳng (d1) và đường thẳng (d2):y=(2m+3)x+3m-1 song song với nhau.
b)Đường thẳng (d1) và đường thẳng (d3):y=x+2m+2 cắt nhau tại một điểm có tung độ bằng 3.
c)Đường thẳng (d1) tiếp xúc với đường tròn tâm O bán kính 2\(\sqrt{2}\)(với O là gốc tọa độ)
Để hàm số y=(m-1)x+4 là hàm số bậc nhất thì \(m-1\ne0\)
hay \(m\ne1\)
a) Để (d1) và (d2) song song với nhau thì \(\left\{{}\begin{matrix}m-1=2m+3\\3m-1\ne4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m-2m=3+1\\3m\ne5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}-m=4\\3m\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-4\\m\ne\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow m=-4\)
Kết hợp ĐKXĐ, ta được: m=-4
Vậy: Để (d1) và (d2) song song với nhau thì m=-4
Đúng 2
Bình luận (0)
Cho đường thẳng d:y=(4m+5)x-2m+7 với m là tham sốa,tìm các giá trị của m để d cùng với 2 đường thẳng d1:y=3x-1 và d2:y=2x+1 đồng quyb,tìm m để d song song với d3:y=-3x+2
Xem chi tiết
a: Tọa độ giao điểm của đường thẳng (d1) và đường thẳng (d2) là:
\(\left\{{}\begin{matrix}3x-1=2x+1\\y=2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2x=2+1\\y=2x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=2\cdot3+1=7\end{matrix}\right.\)
Thay x=3 và y=7 vào (d), ta được:
\(3\left(4m+5\right)-2m+7=7\)
=>\(12m+15-2m=0\)
=>10m=-15
=>m=-3/2
b: để (d)//(d3) thì \(\left\{{}\begin{matrix}4m+5=-3\\-2m+7< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m=-3-5=-8\\-2m< >-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-2\\m< >\dfrac{5}{2}\end{matrix}\right.\)
=>m=-2
Đúng 3
Bình luận (0)
Cho hai đường thẳng có phương trình
y=(m+5)x-2m+3(m≠-5) (1)
y=(2m+1)x+3m(m≠ -1/2) (2)
Tìm các giá trị của m sao cho:
Hai đường thẳng cắt nhau
Hai đường thẳng song song với nhau
Hai đường thẳng trùng nhau
\(\left(1\right)\cap\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5\ne2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne4\\m\ne\dfrac{3}{5}\end{matrix}\right.\\ \left(1\right)//\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3\ne3m\end{matrix}\right.\Leftrightarrow m=4\\ \left(1\right)\equiv\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Đúng 1
Bình luận (0)
a). Để hai hàm số cắt nhau thì:
a≠a'⇒ m+5=2m+1
⇔ m+5=2m+1
⇔ m-2m=1-5
⇔ -m = -4
⇔ m = 4.
Vậy hai hàm số cắt nhau khi m =4.
b). Để hai hàm số song song khi:
\(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m\ne\dfrac{3}{5}\end{matrix}\right.\)
Vậy hai hàm số đó song song khi m=-4; m≠\(\dfrac{3}{5}\).
c). Để hai hàm số trùng nhau khi:
\(\left\{{}\begin{matrix}a=a'\\b=b'\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}m+5=2m+1\\-2m+3=3m\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}m=-4\\m=\dfrac{3}{5}\end{matrix}\right.\)
Vậy hai hàm số đó trùng nhau khi m=-4; m=\(\dfrac{3}{5}\).
Đúng 2
Bình luận (0)
Đường thẳng
y
2
m
+
3
5
x
+
4
7
và đường thẳng
y
5
m
+
2...
Đọc tiếp
Đường thẳng y = 2 m + 3 5 x + 4 7 và đường thẳng y = 5 m + 2 3 x - 1 2 song song với nhau khi m có giá trị là:
A . 1 B . 19 31 C . - 1 19 D . 1 3
Cho hàm số bậc nhất y(2m-1)x-2m+5(m là tham số) có đồ thị là đường thẳng (d) và hàm số y2x+1 có đồ thị là đường thẳng (d)a. tìm giá trị của m để đường thẳng(d) đi qua điểm A(2;-3)b. tìm giá trị của m để đường thẳng(d) song song với đường thẳng (d) .với giá trị m vừa tìm được ,vẽ đường thẳng(d) và tính góc α tạo bởi đường thẳng (d) và trục Ox ( làm tròn đến phút)
Đọc tiếp
Cho hàm số bậc nhất y=(2m-1)x-2m+5(m là tham số) có đồ thị là đường thẳng (d) và hàm số y=2x+1 có đồ thị là đường thẳng (d')
a. tìm giá trị của m để đường thẳng(d) đi qua điểm A(2;-3)
b. tìm giá trị của m để đường thẳng(d) song song với đường thẳng (d') .với giá trị m vừa tìm được ,vẽ đường thẳng(d) và tính góc α tạo bởi đường thẳng (d) và trục Ox ( làm tròn đến phút)
a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)
Đúng 0
Bình luận (0)
Giá trị của m để đường thẳng y = m - 1 x + 2 song song với đường thẳng y = 5 x-2m là
Lời giải:
Để $y=(m-1)x+2$ song song với $y=5x-2m$ thì:
$m-1=5$ và $2\neq -2m$
$\Leftrightarrow m=6$
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để đường thẳng y = (m2 – 3)x + 2m – 3 song song với đường thẳng y = x + 1.
A. m = 2.
B. ![]()
C. m = - 2
D. m = 1.
Đường thẳng y = (m2 – 3)x + 2m – 3 song song với đường thẳng y = x + 1 khi và chỉ khi:

Chọn C.
Đúng 0
Bình luận (0)
Cho hai đường thẳng y = (m+1)x -3 và y = (2m-1)x -5
a) Cmr khi m = \(-\frac{1}{2}\)thì hai hai đường thẳng đó vuông góc với nhau
b) Tìm tất cả các giá trị của m để 2 đường thẳng đó song song với nhau
Giúp mình nha
Cho hai hàm số bậc nhất y = mx + 3 và y = (2m + 1)x – 5
Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau.
b) Hai đường thẳng cắt nhau.
Hàm số y = mx + 3 có các hệ số a = m, b = 3.
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
a) Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
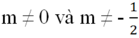
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Vậy đồ thị của hai hàm số là hai đường thẳng song song với nhau khi và chỉ khi a ≠ a' tức là:
m = 2m + 1 => m = - 1
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
b) Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi:
m ≠ 2m + 1 => m ≠ -1.
Kết hợp với điều kiện trên, ta có:
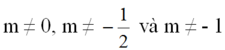
Đúng 1
Bình luận (0)
















