Gieo một con xúc xắc 3 lần. Tính xác suất để tổng số chấm xuất hiện ở 3 lần gieo là một số chẵn

Những câu hỏi liên quan
Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:
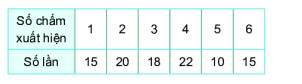
Tính xác suất thực nghiệm của các sự kiện sau:
a. Số chấm xuất hiện là số chẵn;
b. Số chấm xuất hiện lớn hơn 2.
a.
Các số chẵn là 2;4;6
Số lần được 2 là 20, số lần được 4 là 22, số lần được 6 là 15.
Số lần được số chẵn là: 20+22+15=57
Xác suất thực nghiệm của sự kiện “Số chấm xuất hiện là số chẵn” là:\(\frac{{57}}{{100}} = 57\% \)
b.
Các số lớn hơn 2 là 3;4;5;6
Số lần được 3 là 18, số lần được 4 là 22, số lần được 5 là 10, số lần được 6 là 15.
Số lần được số lớn hơn 2 là: 18+22+10+15=65
Xác suất thực nghiệm của sự kiện “Số chấm xuất hiện lớn hơn 2” là:\(\frac{{65}}{{100}} = 65\% \)
Đúng 0
Bình luận (0)
gieo một con xúc xắc hai lần liên tiếp. tính xác suất trong các trường hợp a. lần gieo thứ nhất xuất hiện mặt một chấm b. tổng số chấm hai lần gieo bằng 5 c. hiệu số chấm hai lần gieo bằng 2 d. tích số chấm hai lần gieo là một số lẻ e. tổng số chấm hai lần gieo là một số chia hết cho 3
a: A={(1;1); (1;2); ...; (1;6)}
=>n(A)=6
P(A)=6/36=1/6
b: B={(1;4); (2;3); (3;2); (4;1)}
=>P(B)=4/36=1/9
c: C={(3;1); (4;2); (5;3); (6;4)}
=>P(C)=4/36=1/9
d: D={(1;3); (1;5); (1;1); (3;5); (3;1); (3;3); (5;3); (5;1); (5;5)}
=>P(D)=9/36=1/4
Đúng 1
Bình luận (0)
Gieo 5 lần một con xúc xắc. Tính xác suất để trong 5 lần gieo đó có 3 lần xuất hiện mặt 6 chấm.
gieo một con xúc xắc ba lần. xác suất để trong ba lần gieo có ít nhất 2 lần xuất hiện mặt có số chấm là chẵn Giúp em với ạ. Em đang cần gấp ạ
Có thể là 2 lần chẵn 1 lần lẻ hoặc cả 3 lần đều chẵn
TH1: 2 chẵn, 1 lẻ
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
TH2: 3 lần đều chẵn
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
=>Có 27+27=54 cách
n(omega)=6*6*6=216
=>P=54/216=1/4
Đúng 0
Bình luận (0)
Gieo một con xúc xắc cân đối, đồng chất liên tiếp hai lần. Xét các biến cố sau:A: “Ở lần gieo thứ nhất, số chấm xuất hiện trên con xúc xắc là 1”;B: “Ở lần gieo thứ hai, số chấm xuất hiện trên con xúc xắc là 2”C: “Tổng số chấm xuất hiện trên con xúc xắc ở hai lần gieo là 8”D: “Tổng số chấm xuất hiện trên con xúc xắc ở hai lần gieo là 7”.Chứng tỏ rằng các cặp biến cố A và C; B và C, C và D không độc lập.
Đọc tiếp
Gieo một con xúc xắc cân đối, đồng chất liên tiếp hai lần. Xét các biến cố sau:
A: “Ở lần gieo thứ nhất, số chấm xuất hiện trên con xúc xắc là 1”;
B: “Ở lần gieo thứ hai, số chấm xuất hiện trên con xúc xắc là 2”
C: “Tổng số chấm xuất hiện trên con xúc xắc ở hai lần gieo là 8”
D: “Tổng số chấm xuất hiện trên con xúc xắc ở hai lần gieo là 7”.
Chứng tỏ rằng các cặp biến cố A và C; B và C, C và D không độc lập.
Không gian mẫu là tập hợp số chấm xuất hiện khi gieo con xúc xắc hai lần liên tiếp khi đó \(n\left( \Omega \right) = 6.6 = 36\)
A = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6)} \( \Rightarrow P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}\)
B = {(1; 2); (2; 2); (3; 2); (4; 2); (5; 2); (6; 2)} \( \Rightarrow P\left( B \right) = \frac{6}{{36}} = \frac{1}{6}\)
C = {(2; 6); (3; 5); (4; 4); (5; 3); (6; 2)} \( \Rightarrow P\left( C \right) = \frac{5}{{36}}\)
D = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)} \( \Rightarrow P\left( D \right) = \frac{6}{{36}} = \frac{1}{6}\)
Do đó
\(P\left( A \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( B \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( C \right).P\left( D \right) = \frac{5}{{36}}.\frac{1}{6} = \frac{5}{{216}}\)
Mặt khác
AC = \(\emptyset \Rightarrow P\left( {AC} \right) = 0\)
BC = {(6; 2)} \( \Rightarrow P\left( {BC} \right) = \frac{1}{{36}}\)
CD = \(\emptyset \Rightarrow P\left( {CD} \right) = 0\)
Khi đó \(P\left( {AC} \right) \ne P\left( A \right).P\left( C \right);P\left( {BC} \right) \ne P\left( B \right).P\left( C \right);P\left( {CD} \right) \ne P\left( C \right).P\left( D \right)\)
Vậy các cặp biến cố A và C; B và C, C và D không độc lập.
Đúng 0
Bình luận (0)
bình gieo hai con xúc xắc cùng lúc 50 lần. ở mỗi lần gieo , bình cộng số chấm xuất hiện ở hai con xúc xắc vào bảng sautổng số chấm23456789101112số lần25478754332 tính xác xuất thực nghiệm số lần xuất hiện tổng số chấm ở hai con xúc xắc lớn hơn 6
Đọc tiếp
bình gieo hai con xúc xắc cùng lúc 50 lần. ở mỗi lần gieo , bình cộng số chấm xuất hiện ở hai con xúc xắc vào bảng sau
| tổng số chấm | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| số lần | 2 | 5 | 4 | 7 | 8 | 7 | 5 | 4 | 3 | 3 | 2 |
tính xác xuất thực nghiệm số lần xuất hiện tổng số chấm ở hai con xúc xắc lớn hơn 6
n(B)=8+7+5+4+3+3+2=32
n(omega)=50
=>P(B)=32/50=16/25
Đúng 1
Bình luận (0)
An gieo hai con xúc xắc cùng lúc 80 lần. Ở mỗi lần gieo, An cộng số chấm xuất hiện ở hai xúc xắc và ghi lại kết quả như bảng sau:
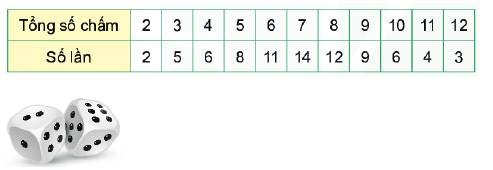
Nếu tổng số chấm xuất hiện ở hai con xúc xắc lớn hơn 6 thì An thắng. Tính xác suất thực nghiệm của sự kiện “An thắng”.
Ta có 14 lần gieo được 7 chấm, 12 lần gieo được 8 chấm, 9 lần gieo được 9 chấm, 6 lần gieo được 10 chấm, 4 lần gieo được 11 chấm và 3 lần gieo được 12 chấm.
Số lần gieo được 7 chấm trở lên là 14 + 12 + 9 + 6 + 4 + 3 = 48 lần.
Do đó số lần An thắng là 48 lần.
Xác xuất thực nghiệm của sự kiện “An thắng” là:\(\dfrac{{48}}{{80}} = \dfrac{3}{5} = \dfrac{3}{5}.100\% = 60\% \)
Đúng 0
Bình luận (0)
Gieo một xúc xắc hai lần liên tiếp. Tính xác suất của mỗi biến cố sau:a) A : Lần thứ hai xuất hiện mặt 5 chấm;b) B : Tổng số chấm xuất hiện trong hai lần gieo bằng 7 ;c) C: Tổng số chấm xuất hiện trong hai lần gieo chia hết cho 3;d) D : Số chấm xuất hiện lần thứ nhất là số nguyên tố;e) E: Số chấm xuất hiện lần thứ nhất nhỏ hơn số chấm xuất hiện lần thứ hai.
Đọc tiếp
Gieo một xúc xắc hai lần liên tiếp. Tính xác suất của mỗi biến cố sau:
a) A : "Lần thứ hai xuất hiện mặt 5 chấm";
b) B : "Tổng số chấm xuất hiện trong hai lần gieo bằng 7 ";
c) C: "Tổng số chấm xuất hiện trong hai lần gieo chia hết cho 3";
d) D : "Số chấm xuất hiện lần thứ nhất là số nguyên tố";
e) E: "Số chấm xuất hiện lần thứ nhất nhỏ hơn số chấm xuất hiện lần thứ hai".
a: n(omega)=36
A={(1;5); (2;5); (3;5); (4;5); (5;5); (6;5)}
=>n(A)=6
=>P(A)=6/36=1/6
b: B={(1;6); (2;5); (3;4); (4;3); (5;2); (6;1)}
=>n(B)=6
=>P(B)=1/6
d: D={(2;1); (2;2); ...; (2;6); (3;1); (3;2); ...;(3;6);(5;1); (5;2);...;(5;6)}
=>P(D)=18/36=1/2
Đúng 1
Bình luận (0)
Bài số 3: Gieo một con xúc xắc. Tính xác suất của mỗi biến cố sau: a) Mặt xuất hiện của xúc xắc có số chấm là số chẵn? b) Mặt xuất hiện của xúc xắc có số chấm là số nhỏ hơn 6?
a: n(omega)=6
n(A)=3
=>P(A)=3/6=1/2
b: n(B)=5
=>P(B)=5/6
Đúng 0
Bình luận (0)















