Đường thẳng d có phương trình dạng chính tắc: \(\frac{x+2}{-1}=\frac{y-3}{4}\)

\(\Rightarrow\) d đi qua điểm \(M\left(-2;3\right)\)

d nhận \(\left(-1;4\right)\) là 1 vtcp

\(\Rightarrow\) d nhận \(\left(4;1\right)\) là 1 vtpt

b/ Phương trình tham số d: \(\left\{{}\begin{matrix}x=-2-t\\y=3+4t\end{matrix}\right.\)

Hệ số góc: \(k=\frac{4}{-1}=-4\)

Câu 2:

Phương trình đoạn chắn của \(\Delta\): \(\frac{x}{2}+\frac{y}{-6}=1\)

Lời giải:

Ta có: \(\overrightarrow{u_d}=(-2,1)\Rightarrow \overrightarrow{n_d}=(1,2)\)

Xét $(d)$: \(\left\{\begin{matrix} x=1-2t\\ y=2+t\end{matrix}\right.\Rightarrow x+2y=5\) (đây chính là pt tổng quát của $(d)$)

$I=(d)\cap (d_1)$ nên: \(\left\{\begin{matrix} x_I+2y_I=5\\ x_I+y_I-3=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x_I=1\\ y_I=2\end{matrix}\right.\)

$M\in Ox$ nên gọi tọa độ của $M$ là $(a,0)$

$MI=\sqrt{(a-1)^2+(0-2)^2}=3$

$\Rightarrow (a-1)^2=5$

$\Rightarrow a=1\pm \sqrt{5}$

Vậy tọa độ $M$ là $(1\pm \sqrt{5}, 0)$

a: vtpt là (4;3)

Phương trình tổng quát là:

4(x-1)+3(y-2)=0

=>4x-4+3y-6=0

=>4x+3y-10=0

b: Phương trình Δ là:

2(x+2)+3(y-4)=0

=>2x+4+3y-12=0

=>2x+3y-8=0

c: Gọi (d): y=ax+b là phương trình cần tìm

Theo đề, ta có:

\(\left\{{}\begin{matrix}-2a+b=1\\3a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{5}\\b=\dfrac{7}{5}\end{matrix}\right.\)

d: Vì (d1)//(d) nên (d1): 3x-5y+c=0

Thay x=4 và y=-2 vào (d1), ta được:

c+3*4-5*(-2)=0

=>c=-22

f: (d): 2x-7y-1=0

=>Δ: 7x+2y+c=0

Thay x=3 và y=5 vào Δ, ta được:

c+21+10=0

=>c=-31

a/ Đường thẳng đã cho nhận \(\left(5;2\right)\) là 1 vtpt

Phương trình tổng quát:

\(5\left(x-1\right)+2\left(y-3\right)=0\Leftrightarrow5x+2y-11=0\)

b/ Đường thẳng đã cho nhận \(\left(3;2\right)\) là 1 vtcp

Phương trình tham số: \(\left\{{}\begin{matrix}x=2+3t\\y=-1+2t\end{matrix}\right.\)

c/ Đường thẳng đã cho có pt:

\(-2\left(x-2\right)+3\left(y+1\right)=0\Leftrightarrow-2x+3y+7=0\)

d/ \(\overrightarrow{AB}=\left(-3;3\right)=-3\left(1;-1\right)\Rightarrow\) đường thẳng nhận \(\left(1;1\right)\) là 1 vtpt

Phương trình:

\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\)

e/ Đường thẳng song song d' nên nhận \(\left(2;-1\right)\) là 1 vtpt

Phương trình:

\(2\left(x-1\right)-1\left(y-4\right)=0\Leftrightarrow2x-y+2=0\)

Bài 2:

a: VTPT là (-1;4)

PTTQ là:

-1(x+3)+4(y-2)=0

=>-x-3+4y-8=0

=>-x+4y-11=0

=>x-4y+11=0

b: Phương trình tổng quát là:

3(x+5)+2(y-2)=0

=>3x+15+2y-4=0

=>3x+2y+11=0

c: vecto CD=(4;3)

=>VTPT là (-3;4)

PTTQ là:

-3(x-5)+4(y-3)=0

=>-3x+15+4y-12=0

=>-3x+4y+3=0

1.

Phương trình:

\(2\left(x-3\right)+1\left(y+4\right)=0\Leftrightarrow2x+y-2=0\)

2.

Phương trình tham số: \(\left\{{}\begin{matrix}x=3-3t\\y=-4+3t\end{matrix}\right.\)

3.

\(\overrightarrow{NM}=\left(4;2\right)=2\left(2;1\right)\)

\(\Rightarrow\) Đường thẳng MN nhận (2;1) là 1 vtcp và (1;-2) là 1 vtpt

Phương trình tổng quát (chọn điểm M để viết):

\(1\left(x-3\right)-2\left(y-4\right)=0\Leftrightarrow x-2y+5=0\)

Phương trình tham số: \(\left\{{}\begin{matrix}x=3+2t\\y=4+t\end{matrix}\right.\)

a) phương trình tổng quát của đường thẳng đi qua \(M\left(1;-2\right)\) có VTPT\(\left(2;3\right)\) là \(2\left(x-1\right)+3\left(y+2\right)=0\) \(\Leftrightarrow2x+3y+4=0\)

vì đường thẳng này nhận \(\overrightarrow{u}\left(2;3\right)\) làm VTPT \(\Rightarrow\) nó nhận \(\overrightarrow{n}\left(3;-2\right)\) làm VTCP \(\Rightarrow\) phương trình tham số của nó là \(\left\{{}\begin{matrix}x=1+3t\\y=-2-2t\end{matrix}\right.\)

b) ta có đường thẳng d nhận \(\overrightarrow{u}\left(-2;1\right)\) làm VTCP \(\Rightarrow\) nhận \(\overrightarrow{n}\left(1;2\right)\) làm VTPT

phương trình tổng quát của đường thẳng đi qua \(N\left(0;-1\right)\) và nhận \(\overrightarrow{n}\left(1;2\right)\) làm VTPT là \(1\left(x-0\right)+2\left(y+1\right)=0\Leftrightarrow x+2y+2=0\)

vì nó nhận \(\overrightarrow{u}\left(-2;1\right)\) làm VTCP \(\Rightarrow\) phương trình tham số của nó là : \(\left\{{}\begin{matrix}x=-2t\\y=-1+t\end{matrix}\right.\)

c) ta có d đi qua điểm M và N \(\Rightarrow\) nó nhận \(\overrightarrow{MN}\left(2;3\right)\) làm VTCP

\(\Rightarrow\) phương trình tham số của đường thẳng đi qua \(M\left(1;-1\right)\) và nhận \(\overrightarrow{MN}\) làm VTCP là : \(\left\{{}\begin{matrix}x=1+2t\\y=-1+3t\end{matrix}\right.\)

ta có d nhận \(\overrightarrow{MN}\left(2;3\right)\) làm VTCP \(\Rightarrow\) d nhận \(\overrightarrow{n}\left(3;-2\right)\) làm VTPT

\(\Rightarrow\) phương trình tổng quát của d là : \(3\left(x-2\right)-2\left(y-3\right)=0\Leftrightarrow3x-2y=0\)

câu d và câu e ) bn chỉ cần tìm VTPT của 2 đường thẳng đó và \(\Rightarrow\) VTCP là ra hết thôi .

gợi ý : đường thẳng \(2x-3y-3=0\) có \(\overrightarrow{u}\left(2;-3\right)\) là VTPT

đường thẳng \(x-y+5=0\) có \(\overrightarrow{n}\left(1;-1\right)\) là VTPT

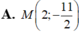
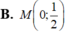
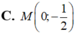
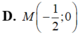
Thế 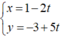 vào phương trình của d’ ta được:

3( 1-2t) -2( -3+5t) -1 =0 hay -16t + 8= 0

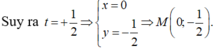
Chọn C.

Điểm M(2; 3) ∈ d

Vectơ chỉ phương của d: vecto u = (1; -2)

⇒ Vectơ pháp tuyến của d: vecto n = (2; 1)

Phương trình tổng quát của d:

d: 2(x - 2) + (y - 3) = 0

⇔ 2x - 4 + y - 3 = 0

⇔ 2x + y - 7 = 0

\(d\) có \(VTCP\overrightarrow{u}=\left(1;-2\right)\Rightarrow VTPT\overrightarrow{n}=\left(2;1\right)\)

qua \(A\left(2;3\right)\)

\(PTTQ\) của d dạng \(a\left(x-x_o\right)+b\left(y-y_o\right)=0\)

\(\Leftrightarrow2\left(x-2\right)+1\left(y-3\right)=0\)

\(\Leftrightarrow2x-4+y-3=0\)

\(\Leftrightarrow2x+y-7=0\)