Cho tam giác ABC, biết AB=6cm, AC=11cm, BC= 8cm. Tính góc B
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
Cho tam giác ABC có AB = 6cm; AC = 8cm; BC = 11cm. Tia phân giác của góc A cắt BC tại M. Tính độ dài các đoạn thẳng MB và MC.
zì tam giác ABC có tia phân giác AM
=>\(\frac{BM}{MC}=\frac{AB}{AC}=\frac{6}{8}=\frac{3}{4}\)(1)
mà BM+MC=11 (2)
Từ 1 zà 2 ta có hệ phương trình
\(\hept{\begin{cases}MB+MC=11\\\text{4MB-3MC=0 }\end{cases}}\)
\(\hept{\begin{cases}MB=\frac{33}{7}\\MC=\frac{44}{7}\end{cases}}\)
cho tam giác ABC có ab=8cm, ac=6cm, bc=10cm a)tam giác ABC là tam giác gì, vì sao b)kẻ ah vuông góc với bc biết bh=6,4cm tính ah,ch
cho tam giác ABC có ab=8cm, ac=6cm, bc=10cm a)tam giác ABC là tam giác gì, vì sao b)kẻ ah vuông góc với bc biết bh=6,4cm tính ah,ch
Tam giác ABC có AB = 6cm, AC = 8cm, BC = 11cm
a) Tính \(\overrightarrow{AB}.\overrightarrow{AC}\) và chứng tỏ rằng tam giác ABC có góc A tù
b) Trên cạnh AB lấy điểm M sao cho AM = 2cm và gọi N là trung điểm của cạnh AC. Tính \(\overrightarrow{AM}.\overrightarrow{AN}\) ?
a) Có \(\overrightarrow{BC}^2=\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{AC}^2+\overrightarrow{AB}^2-2\overrightarrow{AC}.\overrightarrow{AB}\)
Suy ra: \(\overrightarrow{AC}.\overrightarrow{AB}=\dfrac{\overrightarrow{AC^2}+\overrightarrow{AB}^2-\overrightarrow{BC}^2}{2}=\dfrac{8^2+6^2-11^2}{2}=-\dfrac{21}{2}\).
Do \(\overrightarrow{AC}.\overrightarrow{AB}< 0\) nên \(cos\widehat{BAC}< 0\) suy ra góc A là góc tù.
b) Từ câu a suy ra: \(cos\widehat{BAC}=\dfrac{\overrightarrow{AB}.\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|}=-\dfrac{21}{2.6.8}=-\dfrac{7}{32}\).
Do N là trung điểm của AC nên \(AN=AC:2=8:2=4cm\).
\(\overrightarrow{AM}.\overrightarrow{AN}=AM.AN.cos\left(\overrightarrow{AM},\overrightarrow{AN}\right)\)
\(=2.4.cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=2.4.\dfrac{-7}{32}=-\dfrac{7}{4}\).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm. Tính BC, góc B , góc C
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 36 + 64 = 100 (cm)
Suy ra: BC = 100 = 10 (cm)
Ta có: sinC = AB/BC = 6/10 = 0,6
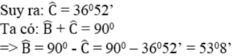
Đúng 0
Bình luận (0)
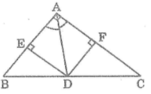
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết A. AC 4cm, BC 8cm, AB 6cmB. AB 4cm, BC 6cm, AC 8cmC. AB 4cm, BC 8cm, AC 6cmD. AB 8cm, BC 4cm, AC 6cm
Đọc tiếp
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết
A. AC = 4cm, BC = 8cm, AB = 6cm
B. AB = 4cm, BC = 6cm, AC = 8cm
C. AB = 4cm, BC = 8cm, AC = 6cm
D. AB = 8cm, BC = 4cm, AC = 6cm
TK
Vậy AB = 4cm, BC = 8cm, AC = 6cm
Đáp án cần chọn là: C
Đúng 5
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 6cm AC = 8cm a/ tính BC b/ kẽ đường phân giác góc A cắt BC tại D tính CD biết BD = 4cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=6cm. AC=8cm a) Tính BC,AH, góc B,góc C b) Vẽ AM là đường trung tuyến của tam giác ABC (M thuộc BC) . Chứng minh góc BAH= góc MAC c) Vẻ HE vuông góc AB (E thuộc AB), HF vuông góc AC (F thuộc AC) . Chứng minh EF vuông góc AM tại K và tính độ dài AK
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC=MB=BC/2
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\left(1\right)\)
\(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAB}+\widehat{ABH}=90^0\)(ΔABH vuông tại H)
Do đó: \(\widehat{ACB}=\widehat{HAB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MAC}=\widehat{HAB}\)
c: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>\(\widehat{AFE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AFE}=\widehat{ABC}\)
\(\widehat{AFE}+\widehat{MAC}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>FE vuông góc AM tại K
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(HA^2=AE\cdot AB\)
=>\(AE\cdot6=4,8^2\)
=>\(AE=3,84\left(cm\right)\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
=>\(AF=\dfrac{4.8^2}{8}=2,88\left(cm\right)\)
Xét ΔAEF vuông tại A có AK là đường cao
nên \(\dfrac{1}{AK^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)
=>\(\dfrac{1}{AK^2}=\dfrac{1}{2,88^2}+\dfrac{1}{3.84^2}\)
=>AK=2,304(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC biết AB = 8cm, BC = 6cm và AC = 10cm. Số đo góc B = …..(độ)