Những câu hỏi liên quan
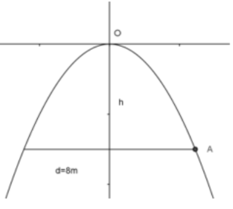
Mặt cắt cổng vào một khu triển lãm có hình dạng một parabol (P): y = -x^2. Mà trục đối xứng OH vuông góc với mặt đất. Biết bề rộng AB của cổng là 4m. Tính chiều cao HO của cổng.
Do tính đối xứng của parabol, \(\Rightarrow H\) là trung điểm AB \(\Rightarrow y_H=y_A=y_B\) đồng thời \(x_A=-x_B\)
Mặt khác \(AB=\left|x_A-x_B\right|=\left|2x_A\right|=4\Rightarrow x_A=2\)
\(\Rightarrow y_A=-x_A^2=-4\Rightarrow y_H=-4\)
\(\Rightarrow OH=\left|y_H\right|=4\) (m)
Đúng 0
Bình luận (0)
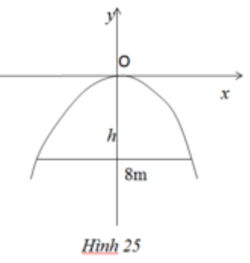
Một chiếc cổng hình parabol dạng y = - x 2 / 2 có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).
Một chiếc cổng parabol có phương trình y = (1/2)x^2. Biết cổng rộng d = 5m. Tính chiều cao của cổng
Một chiếc cổng có hình dạng một phần parabol với chiều
rộng BC d = = 8m(tham khảo hình vẽ). Một người cao 1,65m đứng
thẳng cách chân cổng C một khoảng 45cm thì đỉnh đầu vừa chạm
cổng. Tính gần đúng chiều cao h của cổng.
Để đo chiều cao h của cổng có hình dạng parabol ở trường đại học bách khoa Hà Nội, người ta tiến hành đo khoảng cách L giữa hai chân cổng được L = 9m. Người ta cũng thấy nếu mình đứng cách chân cổng gần nhất là 0,5m thì đầu anh ta chạm vào cổng. Biết rằng người đo cổng cao 1,6m. Hãy tính chiều cao h của cổng parabol?
Một cổng chào có hình parabol cao 10 m và bề rộng của cổng tại chân cổng là 5 m. Tính bề rộng của cổng tại chỗ cách đỉnh 2 m.
Vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Gọi phương trình của parabol là \({y^2} = 2px\)
Ta có chiều cao của cổng \(OH = BK = 10\), chiều rộng tại chân cổng \(BD = 2BH = 5\)
Vậy điểm B có tọa độ là \(B\left( {10;\frac{5}{2}} \right)\)
Thay tọa độ điểm B vào phương trình parabol ta có:
\({\left( {\frac{5}{2}} \right)^2} = 2p.10 \Rightarrow p = \frac{5}{{16}}\), suy ra phương trình parabol có dạng \({y^2} = \frac{5}{8}x\)
Thay \(x = 2\) vào phương trình \({y^2} = \frac{5}{8}x\) ta tìm được \(y = \frac{{\sqrt 5 }}{2}\)
Vậy bề rộng của cổng tại chỗ cách đỉnh 2 m là \(\sqrt 5 \) m
Đúng 0
Bình luận (0)
Một xe tải có chiều rộng 2,4m và chiều cao là 2,5m muốn đi qua một cái cổng có hình Parabol. Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng (đỉnh Parabol) tới chân cổng là 2sqrt{5} m (bỏ qua độ dày của cổng).
a, Trong mặt phẳng tọa độ Oxy, gọi Parabol (P): yax^2 với a0 là hình chiếu biểu diễn cổng mà xe tải muốn đi qua . Chứng minh a-1
b, Hỏi xe tải có đi qua cổng được không ? Tại sao?
Đọc tiếp
Một xe tải có chiều rộng 2,4m và chiều cao là 2,5m muốn đi qua một cái cổng có hình Parabol. Biết khoảng cách giữa hai chân cổng là 4m và khoảng cách từ đỉnh cổng (đỉnh Parabol) tới chân cổng là 2\(\sqrt{5}\) m (bỏ qua độ dày của cổng).
a, Trong mặt phẳng tọa độ Oxy, gọi Parabol (P): y=ax\(^2\) với a>0 là hình chiếu biểu diễn cổng mà xe tải muốn đi qua . Chứng minh a=-1
b, Hỏi xe tải có đi qua cổng được không ? Tại sao?
khi du lịch đến thành phố Xanh lu-i ( Mỹ ) ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới , đó là cổng Ac - xơ. Gỉa sử ta lập một hệ tọa độ Oxy sao cho chân cổng đi qua gốc O ( x,y tính bằng mét ) , chân kia của cỏng ở vị trí ( 162;0 ) . biết một điểm M trên cổng có tọa độ là ( 10;43 ) : a) tìm hàm số bậc 2 có đồ thị chứa cung parabol nói trên ; b) tính chiều cao của cổng ( tính từ điểm cao nhất trên cổng xuống mặt đất , làm tròn kết quả đến hàng đơn vị )
Đọc tiếp
khi du lịch đến thành phố Xanh lu-i ( Mỹ ) ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới , đó là cổng Ac - xơ. Gỉa sử ta lập một hệ tọa độ Oxy sao cho chân cổng đi qua gốc O ( x,y tính bằng mét ) , chân kia của cỏng ở vị trí ( 162;0 ) . biết một điểm M trên cổng có tọa độ là ( 10;43 ) : a) tìm hàm số bậc 2 có đồ thị chứa cung parabol nói trên ; b) tính chiều cao của cổng ( tính từ điểm cao nhất trên cổng xuống mặt đất , làm tròn kết quả đến hàng đơn vị )
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số
A
B
C
D
bằng : A.
1
2
B.
4
5...
Đọc tiếp
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽbên). Tỉ số A B C D bằng :

A. 1 2
B. 4 5
C. 1 2 3
D. 3 1 + 2 2