Cho tam giác ABC, DBC, RBC cân tại D, E, A chung đấy BC.
CM: A, D, E thẳng hàng
Những câu hỏi liên quan
Cho tam giác cân ABC,DBC,EBC chung đáy BC.Chứng minh rằng ba điểm A,D,E thẳng hàng
Vì AB = AC (gt) => A nằm trên đường trung trực của BC
Vì BD = DC (gt) => D nằm trên đường trung trực của BC
Vì BE = EC (gt) => E nằm trên đường trung trực của BC
=> A; D; E cùng nằm trên đường trung trực của BC
=> A ; D ; E thẳng hằng
Đúng 0
Bình luận (0)
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
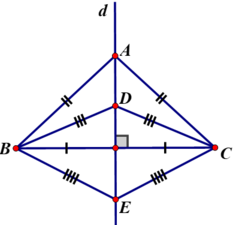
Vì ΔABC cân tại A ⇒ AB = AC
⇒ A thuộc đường trung trực của BC.
Vì ΔDBC cân tại D ⇒ DB = DC
⇒ D thuộc đường trung trực của BC
Vì ΔEBC cân tại E ⇒ EB = EC
⇒ E thuộc đường trung trực của BC
Do đó A, D, E cùng thuộc đường trung trực của BC
Vậy A, D, E thẳng hàng
Đúng 0
Bình luận (0)
Cho ba tam giác cân ABC, DBC, EBC chung đáy BC. Chứng minh rằng ba điểm A, D, E thẳng hàng.
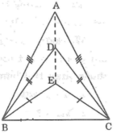
Tam giác ABC cân tại A nên AB = AC
Khi đó A thuộc đường trung trực của BC (1)
Tam giác DBC cân tại D nên DB = DC
Khi đó D thuộc đường trung trực của BC (2)
Tam giác EBC cân tại E nên EB = EC
Khi đó E thuộc đường trung trực của BC (3)
Từ (1), (2) và (3) suy ra: A, D, E thẳng hàng.
Đúng 0
Bình luận (0)
Cho 3 tam giác cân ABC, DBC, EBC có chung đáy BC.Chứng minh ba điểm A, D, E thẳng hàng
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng.
Đúng 0
Bình luận (0)
Gọi d là đường trung trực của đoạn thẳng BC theo định lí 2 :
AB=AC => A thuộc d
DB=DC => D thuộc d
EC=EB => E thuộc d
Các điểm A D E cùng thuộc đường thẳng d. Vậy A D E thẳng hàng
Đúng 0
Bình luận (0)
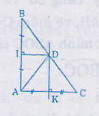
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=>
hay DK là phân giác
=> =
∆ADI = ∆BDI (c.c.c)
=>
=> DI là phân giác
=> =
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay +
= 900
Do đó +
= 900
=> +
= 1800
Đúng 0
Bình luận (0)
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh 3 điểm A, D, E thẳng hàng ?
Hướng dẫn:
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
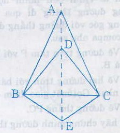
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
Đúng 0
Bình luận (0)
Hướng dẫn:
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
Đúng 0
Bình luận (0)
cho ba tam giác cân ABC;DBC;EBC có chung đáy BC .Chứng minh ba điểm A;D;E thẳng hàng ?
tam giác ABC ; DBC ; EBC lần lượt cân tại đỉnh A; D; E
=> AB = AC => A thuộc đường trung trưc của đoạn thẳng BC
DB = DC => D thuộc đường trung trực của đoạn thẳng BC
EB = EC => E thuộc đường trung trực của đoạn thẳng BC
Vậy A; D; E đều thuộc đường trung trực của đoạn thẳng BC hay A; D; E thẳng hàng
Đúng 0
Bình luận (0)
Cho ba tam giác cân ABC, DBC, EBC chung đáy BC.
Chứng minh rằng ba điểm A, D, E thẳng hàng ?
Vì ∆ABC cân tại A => AB = AC
=> A thuộc trung trực của BC
Vì ∆DBC cân tại D => DB = DC
=> D thuộc trung trực của BC
Vì ∆EBC cân tại E => EB = EC
=> E thuộc trung trực của BC
Do đó A, D, E thuộc đường trung trực của BC nên A, D, E thẳng hàng
Đúng 0
Bình luận (0)
Cho 3 tam giác cân ABC,DBC,EBC có chung đáy BC.Chứng minh 3 điểm A, Đ,E thẳng hàng ( Tự làm nha )
bn tự vẽ hình nha
Xét tam giác ABC cân tại A
\(\Rightarrow\)AB = AC
\(\Rightarrow\)A thuộc trung trực của BC (1)
Xét tam giác DBC cân tại D
\(\Rightarrow\)DB = DC
\(\Rightarrow\)D thuộc đường trung trực của BC (2)
xét ta giác EBC cân tại E
\(\Rightarrow\)EB = EC
\(\Rightarrow\)E thuộc đường trung trực của BC (3)
Từ (1) (2) (3):
\(\Rightarrow\)A , D , E thẳng hàng
~~ hok tốt ~~
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có hai đường phân giác BE và CD (E thuộc AC, D thuộc AB)
a) Chứng minh góc EBC=góc DCB và tam giác DBC= tam giác ECB
b) Qua E vẽ đường thẳng song song với CD cắt tia BC tại điểm F. Chứng minh tam giác BEF cân tại E
c) Chứng minh tam giác DCE= tam giác FEC và BC+DE<2BE.
Giúp mình nha cảm ơn ,mai mình phải nộp bài rồi!
a: \(\widehat{EBC}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{DCB}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{EBC}=\widehat{DCB}\)
Xét ΔDBC và ΔECB có
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
\(\widehat{DCB}=\widehat{EBC}\)
Do đo: ΔDBC=ΔECB
b: Xét ΔBEF có \(\widehat{EBF}=\widehat{EFB}\left(=\widehat{DCB}\right)\)
nên ΔBEF cân tại E
Đúng 0
Bình luận (0)