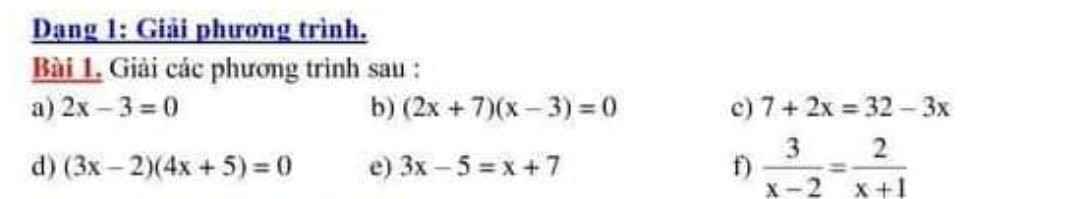
a: Ta có: \(2x-3=0\)

\(\Leftrightarrow2x=3\)

hay \(x=\dfrac{3}{2}\)

b: Ta có: \(\left(2x+7\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+7=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=3\end{matrix}\right.\)

c: Ta có: \(2x+7=32-3x\)

\(\Leftrightarrow5x=25\)

hay x=5

d: Ta có: \(\left(3x-2\right)\left(4x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)

e: Ta có: \(3x-5=x+7\)

\(\Leftrightarrow2x=12\)

hay x=6

f: Ta có: \(\dfrac{3}{x-2}=\dfrac{2}{x+1}\)

Suy ra: \(3x+3=2x-4\)

\(\Leftrightarrow x=-7\left(nhận\right)\)

152 + (-173) - (-18) - 127 

= 152 + (-173) + 18 - 127

= (152 + 18) + (-173) - 127

= 170 + (-300)

= -130

\(152+\left(-173\right)-\left(-18\right)-127\)

\(=\left(152+18\right)-\left(173+127\right)\)

\(=170-300=-130\)

152+(-173)-(-18)-127

=152-173+18-127

=(152+18)-(173+127)

=170-300

=-130

5/ \(10x+3-5x\le14x+12\)
<=>\(10x-5x-14x\le12-3\)
<=>\(-9x\le9\)
<=>\(x\ge-1\)
Vậy bất phương trình có nghiệm là \(x\ge-1\)

6/\(\left(3x-1\right)< 2x+4\)
<=>\(3x-2x< 4+1\)
<=> x<5
Vậy tập nghiệm của bất phương trình là x<5

9/ \(\left(x-1\right)\left(x+2\right)>\left(x-1\right)^2+3\)
<=>\(x^2+2x-x-2>x^2-2x+1+3\)
<=> \(x^2+2x-x-x^2-2x>1+3+2\)
<=>\(-x>6\)
<=> x<-6
Vậy nghiệm của bất pt là X<-6

`(1+2cosx)(3-cosx)=0`

\(\Leftrightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\cosx=3\left(L\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\pi}{3}+k2\pi\\x=\dfrac{-2\pi}{3}+k2\pi\end{matrix}\right.\\ \Leftrightarrow x=\dfrac{2\pi}{3}+k\pi\)

`(k \in ZZ)`

\(\Leftrightarrow\left[{}\begin{matrix}1+2\cos x=0\\3-\cos x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\cos x=-\dfrac{1}{2}\\\cos x=3\end{matrix}\right.\)

Mà \(-1\le\cos x\le1\)

\(\Rightarrow\cos x=-\dfrac{1}{2}\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\pi+k2\pi\\x=\dfrac{4}{3}\pi+k2\pi\end{matrix}\right.\)

Vậy ...

5. 

ĐKXĐ: \(cos\left(x-30^0\right)\ne0\Leftrightarrow x\ne120^0+k180^0\)

Pt tương đương:

\(\left[{}\begin{matrix}tan\left(x-30^0\right)=0\\cos\left(2x-150^0\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-30^0=k180^0\\2x-150^0=90^0+k180^0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=30^0+k180^0\\x=120^0+k90^0\end{matrix}\right.\)

Kết hợp ĐKXĐ: \(\Rightarrow x=30^0+k180^0\)

6.

\(\Leftrightarrow2\sqrt{2}sinx.cosx+2cosx=0\)

\(\Leftrightarrow2cosx\left(\sqrt{2}sinx+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k2\pi\\x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)

5. \(\Leftrightarrow\left[{}\begin{matrix}\tan\left(x-30\right)=0\\\cos\left(2x-150\right)=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x-30=360k\\\left[{}\begin{matrix}2x-150=90+360k\\2x-150=270+360k\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=30+360k\\x=120+180k\\x=210+180k\end{matrix}\right.\)

Vậy ...

6, \(\Leftrightarrow2\sqrt{2}\sin x.\cos x+2\cos x=0\)

\(\Leftrightarrow\cos x\left(1+\sqrt{2}\sin x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\cos x=0\\\sqrt{2}\sin x+1=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{3}{2}\pi+k2\pi\end{matrix}\right.\\x=-\dfrac{\pi}{4}+k2\pi\\x=\dfrac{7}{4}\pi+k2\pi\end{matrix}\right.\)

Vậy ...

bn chụp rung và mờ lắm

36A (Reported speech)

37B

39C

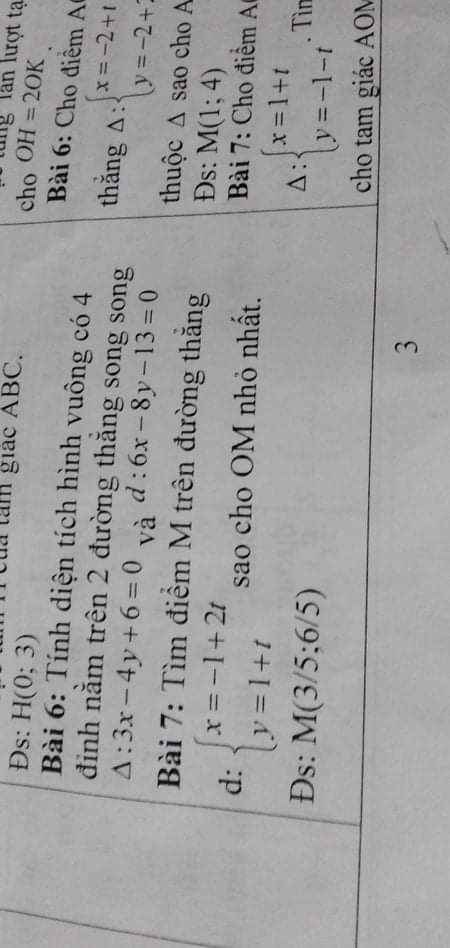
Do M thuộc d nên tọa độ có dạng: \(M\left(2t-1;t+1\right)\)

\(\Rightarrow\overrightarrow{OM}=\left(2t-1;t+1\right)\Rightarrow OM=\sqrt{\left(2t-1\right)^2+\left(t+1\right)^2}\)

\(OM=\sqrt{5t^2-2t+2}=\sqrt{5\left(t-\dfrac{1}{5}\right)^2+\dfrac{9}{5}}\ge\dfrac{3}{\sqrt{5}}\)

Dấu "=" xảy ra khi \(t-\dfrac{1}{5}=0\Rightarrow t=\dfrac{1}{5}\Rightarrow M\left(-\dfrac{3}{5};\dfrac{6}{5}\right)\)

Đáp án của bài toán bị sai (nhầm dấu hoành độ)