Giúp em đi gấp lắm rồi

Những câu hỏi liên quan
giúp em câu này đi em gấp lắm rồi ạ
Đọc tiếp
giúp em câu này đi em gấp lắm rồi ạ
Lời giải:
Vì $(d_2)$ có hệ số góc là $3$ nên $m=3$
$(d_2)$ cắt trục hoành tại điểm có hoành độ $-2$, nghĩa là $(d_2)$ đi qua $(-2;0)$
$\Rightarrow 0=m.(-2)+n=3(-2)+n$
$\Rightarrow n=6$
Vậy $m=3; n=6$
Đúng 0
Bình luận (1)
Tìm GTLN,GTNN của hàm số y= ║x ²-6x+5 ║/[2;4] mọi người giúp em đi em gấp lắm rồi
 giúp em vs ạ đang gấp lắm sắp đi học rồi , ai trl nhanh mik tik cho ạ , please mn ☹
giúp em vs ạ đang gấp lắm sắp đi học rồi , ai trl nhanh mik tik cho ạ , please mn ☹
a. Số lít nước trong bể là
\(2,5\times1,5\times1,2=4,5\left(m^3\right)\)
Đổi 4,5 m3 = 4500 dm3
Vậy trong bể có 4500 l nước
b.Chiều cao của mực nước trong bể là
\(1,2\times\dfrac{2}{5}=0,48\left(m\right)\)
Chiều cao mực nước cách miệng bể là
\(1,2-0,48=0,72\left(m\right)\)
Đúng 1
Bình luận (0)
giúp em vs ạ đang rất là gấp sắp đi học rồi , ai trl nhanh em sẽ tik cho please mn
Đúng 0
Bình luận (0)
giúp mình đi mình gấp lắm rồi
 Mọi người giúp em với, em cần gấp lắm rồi :((
Mọi người giúp em với, em cần gấp lắm rồi :((
Bài 2:
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc 1 đường tròn(1)
Xét tứ giác OHAC có
\(\widehat{OHA}+\widehat{OCA}=180^0\)
Do đó: OHAC là tứ giác nội tiếp
=>O,H,A,C cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra A,B,H,O,C cùng năm trên 1 đường tròn
b: \(\widehat{BHA}=\widehat{BOA}\)
\(\widehat{CHA}=\widehat{AOC}\)
mà \(\widehat{AOB}=\widehat{AOC}\)
nên \(\widehat{BHA}=\widehat{CHA}\)
hay HA là tia phân giác của góc BHC
Đúng 1
Bình luận (1)
mọi người giúp đi ạ, mình cần gấp lắm rồi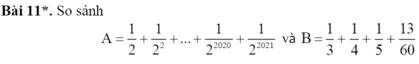
Giải nhanh giúp em với ạ em đang cần gấp lắm rồi
Bài 5:
\(x^2+y^2+1\ge xy+x+y\)
\(\Leftrightarrow2\left(x^2+y^2+1\right)\ge2\left(xy+x+y\right)\)
\(\Leftrightarrow2x^2+2y^2+2\ge2xy+2x+2y\)
\(\Leftrightarrow2x^2+2y^2+2-2xy-2x-2y\ge0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2\ge0\left(đúng\right)\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=1\)
Đúng 0
Bình luận (0)
GIÚP EM CÂU C BÀI 2 VÓI ẠAAA,EM CẦN GẤP LẮM RỒI Ạ
Mọi người giúp em câu 3 với ạ, em đang cần gấp lắm rồi :((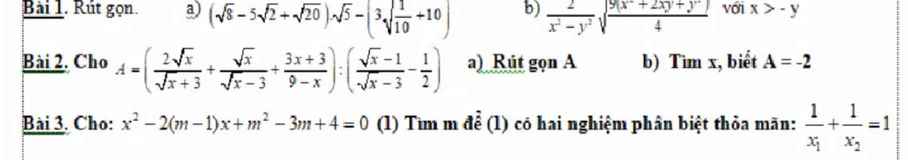
Câu 3:
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m+4\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-3m+4\right)\)
\(=4m^2-16m+4-4m^2+12m-16=-4m-12\)
Để phương trình có hai nghiệm phân biệt thì -4m-12>0
=>-4m>12
hay m<-3
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+4\end{matrix}\right.\)
Theo đề, ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow m^2-3m+4-2m+2=0\)
=>(m-2)(m-3)=0
hay \(m\in\varnothing\)
Đúng 1
Bình luận (0)


















